september 28, 2008

Constraint programming: Fler MiniZinc-modeller, t.ex. Martin Gardner och nonogram

Förutom att ha lekt med de Javabaserade villkorsprogrammeringssystemet Choco version 2 har även några MiniZinc-modeller skapats sen sist.

Förra gången räknades till cirka 360 modeller (stora eller små). Nu är det cirka 440 stycken (stora och små), vilket innebär cirka 80 nya modeller. Som vanligt finns de på My MiniZinc page. De läggs upp där så fort som de är klara, så om du är intresserad av nya modeller är det bara att - mer eller mindre - regelbundet kolla den sidan.

Denna gång har det blivit en del problem från husguden Martin Gardner, mest beroende på att jag håller på att beta av samlingen med Martin Gardners pyssel i The Colossal Book of Short Puzzles and Problems, (ISBN: 9780393061147, sammanställd av Dana Richards).

Personliga favoriter
* nonogram.mzn, även känd som "painting by numbers". Utifrån rad- och kolumnsummor ska man skapa bilder. Jämför med "discrete tomography" som nämndes i Några fler MiniZinc-modeller, t.ex. Smullyans Knights and Knaves-problem samt med "Survo puzzle" som nämndes i Nästan 36 modeller med villkorsprogrammering (constraint programming) i MiniZinc.
* two_cube_calendar.mzn: Two cube calendar. Till synes enkelt problem, men det var trixigt att modellera eftersom en siffra kan användas på två olika sätt.
* diffn.mzn. Placering av boxar utan att de överlappar varandra. Stödjer tre olika representationer (vilket tyvärr gör modellen lite svåröverskådlig).
* calculs_d_enfer.mzn: Calculs d'enfer. Yet another alfametiskt problem med några twistar: här används även negativa värden och man ska minimera det största absolutvärdet. En viktig sak är att använda korrekt heuristik annars går det långsamt att lösa problemet: den snabbaste jag hittade var "occurrence" respektive "indomain_max".


Martin Gardner
Detta är några problem från de första kapiteln av (den ovan nämnda) The Colossal Book of Short Puzzles and Problems. En bok att rekommendera. Man noterar redan på de första sidorna (om man inte läst Gardner tidigare för då vet man troligen detta redan) att en del standardexempel - t.ex. SEND + MORE = MONEY, Langfords heltalssekvens - beskrevs eller populariserades av Martin Gardner.

Nedanstående har det gemensamma kännetecknet att de - mig veterligen - inte modellerats i MiniZinc. I vissa fall har jag inte sett någon diskussion alls på nätet (i alla fall inte under dessa namn).

curious_set_of_integers.mzn: Curious set of integers
divisible_by_7.mzn: Divisible by 7
gardner_prime_puzzle.mzn: Prime puzzle
magic_squares_and_cards.mzn: Magic squares and cards
nine_digit_arrangement.mzn: Nine digit arrangements
nine_to_one_equals_100.mzn: Nine to one equals 100
nonogram.mzn
pool_ball_triangles.mzn: Pool ball triangles
two_cube_calendar.mzn: Two cube calendar


Andra pyssel och matematiska gåtor
bank_card
calculs_d_enfer.mzn: Calculs d'enfer puzzle (from the NCL manual), se kommentar ovan
coins_problem.mzn: Minimize the number of coins...
family_riddle.mzn: Family riddle
magic_hexagon.mzn: Magic hexagon
message_sending: Message sending


Operations research, linear programming, integer programming
lectures: ett scheduleringsproblem
scheduling_chip: ännu ett scheduleringsproblem


Non linear problems
spreadsheet.mzn, exempel på problem som ofta löses i spreadsheets


Combinatorics
maximum_subarray.mzn: Maximum subarray
set_packing.mzn, set packing
set_covering_skiena.mzn, set covering (ännu ett exempel)
all_paths_graph.mzn, skapa vägar med utgångspunkt från en grafrepresentation


Global constraints
Som vanligt har även några global constraints modellerats. Förutom att många av dem är nyttiga i sig, är modelleringen av dem en nyttig övning. (Nu finns det cirka 100 global constraints modellerade, endast en tredjedel av den fulla listan. I och för sig är cirka 40-50 global constraints redan definierade i MiniZinc, antingen inbyggda eller i global.mzn, men det är i alla fall en massa kvar...)

contains_array
cumulative_test
diffn
discrepancy
disjunctive
domain
domain_constraint
imply
in_interval
in_set
indexed_sum
inverse_within_range
ith_pos_different_from_0
k_same
k_same_modulo
lex2
lex_between
lex_chain_less
lex_different
lex_greater
max_index
min_index
nclass
open_alldifferent
product_test
roots_test
same_interval
same_modulo
shift
sliding_sum
sliding_time_window
sliding_time_window_from_start
smooth
soft_same_var
sort_permutation
weighted_sum (not in the catalogue)


Prolog/constraint logic programming benchmarks
Här är några benchmarks för Prolog eller constraint programming som inte tidigare modellerats i MiniZinc.

crossbar.mzn
crypta.mzn
eq10.mzn
fractions.mzn
grocery2.mzn
magic3.mzn
magic4.mzn
multipl.mzn
olympic.mzn
parallel_resistors.mzn
sudoku_25x25_250.mzn
voltage_divider.mzn


Övrigt
fizz_buzz Liten programmeringsövning
huey_dewey_louie, litet logiskt problem
power, variant av power-funktionen (som ännu inte funkar i MiniZinc)

Posted by hakank at 08:17 EM Posted to Constraint Programming | Matematik | Pyssel

juli 20, 2008

Fler constraint programming-modeller i MiniZinc, t.ex. Minesweeper och Game of Life

Här är några fler MiniZinc modeller som skapats sedan sist. För en fullständig lista över samtliga publicerade modeller, se My MiniZinc page.

I samtliga modeller anges referenser, inspiration etc.

Personligen tycker jag följande modeller är lite kul:
* Minesweeper (som presenteras speciellt nedan)
* Game of Life
* Quasigroup completion problem (se nedan för ett antal testproblem)
* Födelsedagsproblemet


Minesweeper


Tänkte nämna något mer om Minesweeper.

Modellen till Minesweeper är - möjligen förvånansvärt - enkel. Notera att man s.a.s. "räknar baklänges": genom att summera minorna (mines) för att få de värden som ges i problemet (game). Sådant är typiskt i constraint programming.


% MiniZinc model for Minesweeper.
int: r; % rows
int: c; % column
int: X = -1; % the unknowns

% encoding: -1 for unknown, >= 0 for number of mines in the neighbourhood
array[1..r, 1..c] of -1..8: game;
array[1..r, 1..c] of var 0..1: mines;

constraint
forall(i in 1..r, j in 1..c) (
(
(game[i,j] >= 0 )
->
game[i,j] = sum(a,b in {-1,0,1} where
i+a > 0 /\ j+b > 0 /\
i+a <= r /\ j+b <= c
)
(mines[i+a,j+b])
)
/\
(game[i,j] > X -> mines[i,j] = 0)
/\
(game[i,j] = X <- mines[i,j] = 1)
)
;

Ett exempelproblem, där ett tal anger hur många bomber det finns som grannar och X att vi inte vet något om rutan (det kan vara en bomb men behöver inte vara det).

% Minesweeper example
r = 6;
c = 6;
game = array2d(1..r, 1..c, [
X,X,2,X,3,X,
2,X,X,X,X,X,
X,X,2,4,X,3,
1,X,3,4,X,X,
X,X,X,X,X,3,
X,3,X,3,X,X,
]);

Lösningen - som kommer blixsnabbt - är följande. Positionerna av bomberna markeras med 1.

1 0 0 0 0 1
0 1 0 1 1 0
0 0 0 0 1 0
0 0 0 0 1 0
0 1 1 1 0 0
1 0 0 0 1 1

Minesweeper har visats vara ett s.k. NP-komplett problem, dvs ohyggligt svårt att lösa generellt för godtyckligt stora problem. De exempel som används i modellen är dock så (förhållandevis) små att lösningen kommer direkt.

Se vidare
Richard Kaye's Minesweeper Pages
Minesweeper (Wikipedia)
Ian Stewart on Minesweeper
The Authoritative Minesweeper: Articles and Announcements

Automatisk "lösning" av Minesweeper i Mozart/Oz där fler referenser ges.

Övriga modeller

Här är de övriga modellerna, grupperade enligt samma princip som på My MiniZinc page.

Puzzles, small and large

Global constraints

Operations research, linear programming, integer programming

Combinatorial problems

Other models


Posted by hakank at 08:23 EM Posted to Constraint Programming | Matematik | Pyssel

juli 07, 2008

Fler MiniZinc modeller kring recreational mathematics

I Martin Chlond's Integer Programming Puzzles i MiniZinc förevisades MiniZinc-modeller för Martin Chlonds Integer Programming Puzzles.

Här är några fler i samma stil (recreational mathematics) som jag just har lagt upp på min Minizinc-sida . Det är MiniZinc-modeller baserade på Chlonds Puzzle artiklar (och de där ingående integer programming-modellerna) i INFORMS Transactions on Education (en öppen tidskrift om operational research).


Och så några andra recreational mathematics modeller som publicerades samtidigt:

Posted by hakank at 07:53 EM Posted to Constraint Programming | Matematik | Pyssel

juni 29, 2008

Gruppteoretisk lösning av M12 puzzle i GAP

I Tre matematiska / logiska pyssel med constraint programming-lösningar: n-puzzle, SETS, M12 (i MiniZinc) presenterades det gruppteoretiska pysslet M12, då med en lösning i MiniZinc (modellen M12.mzn).

När jag läste om M12 tänkte jag att det skulle vara skoj med även en gruppteoretisk lösning eftersom det är ett gruppteoretiskt problem. En sådan lösning har nu gjorts med hjälp av det abstrakta algebraiska systemet GAP. Numera finns GAP även med i distributionen av det öppna matematiska (och mycket trevliga) systemet Sage.

Uppdatering
Efter lite funderande kom jag på en bättre lösning. I stället för att ändra en massa i denna text skrev jag en ny: Gruppteoretisk lösning av M12 puzzle i GAP - take 2, vilken se.


Kort beskrivning av M12
Som tidigare beskrivits går M12-pysslet ut på att man har en sekvens av 12 siffror i en härlig oordning och man ska med hjälp av två operationer återställa sekvensen till 1,2,3,4,5,6,7,8,9,10,11,12. Operationerna är:
Merge: [1, 12, 2, 11,3, 10, 4, 9, 5, 8, 6, 7] blir [1,2,3,4,5,6,7,8,9,10,11,12].
Inverse: Vänder listan om, [1,2,3,4,5,6,7,8,9,10,11,12] blir [12,11,10,9,8,7,6,5,4,3,2,1]. Not, jag kallar operationen (av historiska skäl) för Reverse här nedan.


GAP-program
Här är GAP-programmet (M12_gap.txt). Resultat från ett kommando eller kommentar skrivs efter "#".


Först definierar vi operatorerna, dvs generatorerna i gruppen. Här används PermList som tar en lista och skapar en permutationscykel.

#
# Solving the M12 for a specific sequence
#

#
# Define the operators
#

# Reverse (Inverse)
reverse := PermList([12,11,10,9,8,7,6,5,4,3,2,1]);
# (1,12)(2,11)(3,10)(4,9)(5,8)(6,7)

# Merge
merge := PermList([1,12,2,11,3,10,4,9,5,8,6,7]);
# (2,12,7,4,11,6,10,8,9,5,3)

Skapa gruppen g och gör några tester.


# Create the group
g:=Group([reverse, merge]);
# Group([ (1,12)(2,11)(3,10)(4,9)(5,8)(6,7), (2,3,5,9,8,10,6,11,4,7,12) ])

# Which group is it?
StructureDescription(g);
# "M12"

Size(g);
# 95040

Bra, det är alltså gruppen M12, dvs Mathieu-grupp av ordningen 12. Notera att det finns ett inbyggt kommando för att skapa en Mathieugrupp (MathieuGroup), men den har inte de generatorer som vil ska använda, alltså rullar vi vår egen.


Nu börjar det roliga. Låt oss som exempel ta följande sekvens som nyss skapats av M12-programmet.


#
# Create the puzzle to solve
#
puzzle:=[4, 5, 11, 1, 9, 6, 3, 10, 2, 7, 12, 8];;


För att få reda på lösningen görs en "faktorisering", med hjälp av funktionen Factorization.


Factorization(g, PermList(puzzle)^-1);
# x1*x2^2*x1*x2^-5*x1*x2^-5

Här har vi en lösning som ska tolkas som operationer i pysslet:

x1*x2^2*x1*x2^-5*x1*x2^-5

x1 betyder den första generatorn (dvs Reverse/Inverse) och x2 är Merge.

Det finns två saker att tänka på här:
- man ska läsa sekvensen baklänges
- alla operationer med negativ exponent måste konverteras till en positiv exponent. Det görs med en enkel subtraktion: x2^-5 innebär samma sak som x2^(11-5) = x2^6

Om vi översätter enligt ovanstående två regler blir det:

x2^6 x1 x2^6 x1 x2^2 x1

Så, uttolkat i samma form som M12-applikationen blir lösningen följande. Tänk på att vi arbetar med lösningen bakifrån och att x1 är I och x2 är M:

M6 I M6 I M2 I

Detta är en lösning med 6+1+6+1+2+1 = 17 steg.


En variant

Förutom Factorization finns det en annan metod, och det är den som generellt rekommenderas för att göra denna typ av "faktoriseringar". Tyvärr tenderar den att generera längre lösningar än med Factorization.


#
# This is the recommended function for factorizations, but it gives longer
# solutions (strings) than Factorization.
#

#
# Create names to identify the operations
#
M:=g.2; R:=g.1;
hom:=EpimorphismFromFreeGroup(g:names:=["R","M"]);

#
# Now, solve the puzzle
#
PreImagesRepresentative(hom,PermList(puzzle)^-1);
# M^-3*R^-1*M^4*R^-1*M*R*M^3*R*M^-3*R*M^-1*R*M^2

Lösningen är alltså:

M^-3*R^-1*M^4*R^-1*M*R*M^3*R*M^-3*R*M^-1*R*M^2

Notera att R^-1 ska tolkas som en Inverse-operation.

Ovanstående motsvarar följande M12-operationer:

M2 I M10 I M8 I M3 I M I M4 I M8

Detta är en lösning på 2 + 1 + 10 + 1 + 8 + 1 + 3 + 1 + 1 + 1 + 4 + 1 + 8 = 42 steg, vilket är mycket längre än Factorization-approachen.


Man bör notera att dessa faktoriseringar är optimerade att få så små exponenter som möjligt oavsett om det är positiva eller negativa exponenter. Vi är dock endast intresserade av positiva exponenter och lider därför av denna optimering.

Om man adderar exponenterna utan tecken, ger Factorization i alla fall en enklare lösning.

Factorization: x1*x2^2*x1*x2^-5*x1*x2^-5 = 1 + 2 + 1+ 5 +1+ 5 = 15 steg.

PreImagesRepresentative: M^-3*R^-1*M^4*R^-1*M*R*M^3*R*M^-3*R*M^-1*R*M^2 = 3 + 1 + 4 + 1 + 1+ 3+ 1 + 3+ 1+ 1 + 1 + 2 = 22 steg.


Båda dessa faktoriseringar går mycket snabbt, typ någon sekund eller så.


Jämförelse med MiniZinc-lösningen
Jag testade att köra pysslet med MiniZinc-modellen M12.mzn. Den tar väldigt lång tid (typ 10-tals minuter) och ger följande lösning på 18 steg, dvs något sämre än Factorization-varianten. Operatorn 1 motsvarar Merge och operatorn 2 motsvarar Inverse.


2, 1, 1, 1, 1, 1, 1, 2, 1, 1, 2, 1, 2, 1, 1, 1, 2

dvs operationerna: R M6 R M2 R M R M3 R M

Så här ser sekvensen ut för respektive operation. Siffran till vänster är operationen. Första raden är ursprungssekvensen och är endast med för presentationens skull.


0: 4 5 11 1 9 6 3 10 2 7 12 8
2: 8 12 7 2 10 3 6 9 1 11 5 4
1: 8 7 10 6 1 5 4 11 9 3 2 12
1: 8 10 1 4 9 2 12 3 11 5 6 7
1: 8 1 9 12 11 6 7 5 3 2 4 10
1: 8 9 11 7 3 4 10 2 5 6 12 1
1: 8 11 3 10 5 12 1 6 2 4 7 9
1: 8 3 5 1 2 7 9 4 6 12 10 11
2: 11 10 12 6 4 9 7 2 1 5 3 8
1: 11 12 4 7 1 3 8 5 2 9 6 10
1: 11 4 1 8 2 6 10 9 5 3 7 12
2: 12 7 3 5 9 10 6 2 8 1 4 11
1: 12 3 9 6 8 4 11 1 2 10 5 7
2: 7 5 10 2 1 11 4 8 6 9 3 12
1: 7 10 1 4 6 3 12 9 8 11 2 5
1: 7 1 6 12 8 2 5 11 9 3 4 10
1: 7 6 8 5 9 4 10 3 11 2 12 1
2: 1 12 2 11 3 10 4 9 5 8 6 7
1: 1 2 3 4 5 6 7 8 9 10 11 12 % Solution!

Posted by hakank at 08:25 EM Posted to Constraint Programming | Matematik | Pyssel

augusti 19, 2007

Recension av Keith Devlin, Gary Lorden: The Numbers Behind Numb3rs: Solving Crime with Mathematics

TV-serien Numb3rs handlar om bröderna Don, FBI-agent, och den yngre brodern Charlie som är en matematikprofessor. Charlie är den egentlige "hjälten" i serien där hans matematiska begåvning (genialitet!) gör att Don kan lösa sina fall. Speciellt skoj är att matematiken i TV-serien är central och man har gjort sig möda om att göra den så korrekt som möjligt. Inte speciellt förvånande (för mina reguljära läsare) är serien en stor favorit.

Serien ska strax börja på fjärde säsongen och då passar det utmärkt att en bok om (kring) serien kommer ut. Det är matematikerna Keith Devlin och Gary Lorden som skrivit The Numbers Behind Numb3rs: Solving Crime with Mathematics (ISBN: 9780452288577) som gör en populärvetenskaplig exposé över matematiken som används i serien.

De två författarna är väl lämpade att skriva boken:
Keith Devlin, professor i matematik och är nog mest känd som Math Guy och skriver i den (populär)matematiska kolumnen Devlin's Angle (Archives). Devlin har även skrivit flera böcker (där 1988 års utgåva av Mathematics - the New Golden Age var en stor inspirationskälla för mitt matematikintresse).

Gary Lorden kände jag däremot inte till innan serien Numb3rs. Han är professor i matematik och "chief mathematics consultant" till TV-serien. Den senare rollen beskrivs t.ex. i CaltechNews-artikeln Crime and Computation.

Boken är "oteknisk" skriven och det krävs inga speciella matematiska förkunskaper (förutom sådana som normal skolgång bör ha gett). Det finns få formler/ekvationer och de som finns förklaras nästan alltid ingående.

När jag först läste om boken trodde jag att alla kapitel skulle behandla Numb3rs-relaterade saker och endast sådana. Man har istället valt en mer utökad variant och det saknas Numb3rs-koppling i några kapitel, t.ex. kapitel 5, "Image Enhancement and Reconstruction" som handlar om bildbearbetning i samband med efterverkningarna av lynchningen av Rodney King. Det görs också intressanta genomgångar av matematiken i och kring rättegångarna (som inte alls är med i TV-serien), t.ex. bevisvärdet av DNA-test och fingeravtryck samt kring urvalet av jurys. Denna utökning fungerar bra, även om det möjligen kan vara lite förledande i marknadsföringen.

En av de stora fördelarna med populärvetenskapliga böcker är att man blir inspirerad att läsa vidare i det ämne som behandlas. Tyvärr försvåras sådan vidareläsning genom att det i många kapitel inte finns några litteraturreferenser eller vidareläsningstips (det finns dock flera kapitel som har mycket referenser). Möjligen har författarna ansett att läsarna själv söker efter obekanta termer via sökmotorer eller Wikipedia. Fel approach enligt min mening.

Trots bristerna tycker jag om boken och rekommenderar den till de som också gillar TV-serien. Och rekommenderar TV-serien för den som inte sett den.

Bokens kapitel
Här är en listning av kapiteln och några kommentarer kring dem.


Se även
Devlins artikel om TV-serien NUMB3RS gets the math right.

Jag har köpt de två första säsongerna från Discshop. Tyvärr saknas här de kommentatorspår som finns i region 1-varianterna.

Recensionen New Book Explains How Math Can Help Solve Crimes finns även som pratversion inklusive författarnas (autentiskt återgivna förutsätter jag) röster.

Sajten Redhawke NUM3RS med länkar till matematiska begrepp

Dr. Andrew Nestler's Analysis of NUMB3RS

Min favoritblogg i Numb3rsiana: num3rs blog

Succén med TV-serien har även knoppat ett samarbete mellan CBS, Texas Intstrument och National Council of Teachers of Mathematics i form av sajten We All Use Math Every Day där lärare kan hämta material som kopplas till de olika avsnitten. Aktiviteter för respektive säsong (sorterad i bloggordning):
Season 1
Season 2
Season 3

Posted by hakank at 11:21 FM Posted to Böcker | Machine learning/data mining | Matematik | Social Network Analysis/Complex Networks

juli 23, 2007

Terence Tao videoföreläsning 'Structure and Randomness in the Prime Numbers' (matematik, talteori)

Terence Tao anses vara en av matematikens klarast lysande stjärnor. Enligt artikeln Terence Tao: The "Mozart of Math":


"Terry is like Mozart -- except without Mozart's personality problems," said John Garnett, professor and former chair of mathematics in the UCLA College. "Mathematics just flows out of him." "Mathematicians with Terry's abilities appear only once in a generation," said Garnett. "He's probably the best mathematician in the world right now. Terry can unravel an enormously complicated mathematical problem and reduce it to something very simple. We're amazingly lucky to have him at UCLA."


Hans videoföreläsning Structure and Randomness in the Prime Numbers (.smil videoformat) är en populärt hållen och mycket trevlig föreläsning om talteori, t.ex. primtalstvillingar och Riemann-hypotesen (som anses vara ett av de knepigaste matematiska problemen). Slides (PDF).

(Not: Jag hade lite problem med att videoströmmen slutade att strömma efter cirka 8 minuter och efter cirka 35 minuter. Det vara bara att starta om på nytt. Ibland funkade det att snabbspola, men inte alltid.)


Se även
Taos blogg What's new (som ersätter den gamla "proto-bloggen" What's new)
Information for media, en samling av artiklar om Tao
En kort TV-biografi (strömmande bilder, alltså)
Några kapitel (.ps-fil) från boken Solving Mathematical Problems: A personal perspective. Och kan beställas t.ex. här (ISBN: 9780199205608).


(Via den relativt nyfunna favoritbloggen God Plays Dice.)

Posted by hakank at 06:18 EM Posted to Matematik | Video podcasts | Comments (1)

februari 19, 2007

Den som ändå bodde kring Uppsala: 1 mars pratar Persi Diaconis om matematik och trolleri

Den 1 mars 2007 är det Celsius-Linneföreläsning å Uppsala Universitet. Celsius-föreläsningen är Persi Diaconis som föreläser om Mathematics and magic tricks

bulletin.se-notisen Trollkonster och empatiska djur på årets Celsius-Linnéföreläsningar beskriver ner:


Celsiusföreläsningen hålls av Persi Diaconis, professor i statistik och matematik vid Stanford University. Diaconis har använt matematiken för att utveckla magiska trick, och är bland annat känd för att ha bevisat att en vanlig kortlek måste blandas sju gånger för att vara ordentligt blandad. Sättet på vilket magiska trick fungerar är minst lika fascinerande som tricken själva, menar han, och kommer att visa detta bland annat genom att demonstrera några trick.

Är det någon besökare som vill ta anteckningar och publikt (eller privat) delge dem?


(Det finns fler Linnéevenemang.)

Posted by hakank at 05:57 EM Posted to Husgudar | Matematik | Trolleri, magi etc | Comments (4)

oktober 22, 2006

Dagslänkar 2006-10-22 - Om senaste avsnittet av numb3rs

Om senaste numb3rs-avsnittet ("Traffic").

numb3rs blog: Traffic as a fluid flow

The Econophysics Blog: Randomness & the 'Ludic Fallacy' on Numb3rs

Texas Instrument har en sajt kring TV-serien:
We All Use Math Every Day, där t.ex. Activities med länkar till nedladdningsbara PDF-filer etc.

Posted by hakank at 09:33 FM Posted to Matematik

juli 10, 2006

Ytterligare forskning kring fotboll

Jaha, nu är VM-fotbollen över och det kommer nog att kännas lite tomt kring 21-tiden de närmsta dagarna. Kul att ha sett de flesta matcherna, med eller utan bok att ta till i de få fall då det varit riktigt tråkigt.


Under de gångna veckorna har några fotbollsforskningslänkar samlats på hög och det är dags att rensa.

Slate: World Cup Game Theory - What economics tells us about penalty kicks., av Tim Hartford som skriver kolumnen The Undercover Economist och för övrigt ganska nyss kommit ut med boken The Undercover Economist (ISBN: 0316731161), och som ännu nyssare erhållits.

Gelf Magazine: The Game Theory of Penalty Kicks

The Sports Economist: Tinkering with the World Cup
The Sports Economist: Statistical analysis of World Cup fouls

Ivars Peterson MathTrek-artikel om den nya konstruktionen av bollen: Bending a Soccer Ball

The Econophysics Blog: Predictive Markets for the World Cup?

Freakomonics Blog: What can the World Cup teach us about markets?
Freakonomics Blog: In soccer, it is not whether you win or lose, but how you play the game
Are stars born or made? Here’s what World Cup 2006 has to say on the issue.
Marginal Revolution: Why I find soccer boring

Bok: John Wesson The Science of Soccer (ISBN: 0750308133) som handlar om både fysikaliska delarna av fotboll (t.ex. vinklar och krafter) och mer matematiska, t.ex. spekulation i varför planen respektive målen är av de mått som de har (formel gives), om straffläggning etc. Har endast bläddrat i boken, men den verkar spännande.


Se även
Mer om forskning kring fotboll
Straffsparkar i fotboll och annan fotbollsmatematik
Optimering av fotbollstittande


Andra bloggar om: .

Posted by hakank at 11:20 FM Posted to Matematik | Spelteori och ekonomi | Sport, idrott, hälsa

juni 26, 2006

Mer om forskning kring fotboll

I Studio Ett intervjuades nyss Patric Andersson, forskare vid Handelshögskolan: Finns det psykologiska mål? Vi gör ett försök att skilja mellan myter och sanningar i alla påståenden dessa dagar om fotboll, världens största sport. Patric Andersson, forskare vid Handelshögskolan deltar.. Djuplänk.

Presentation av Patric Anderssons forskning finns t.ex. i pressmeddelandet Forskning slår hål på myter om fotbollens ekonomi och psykologi. Den workshop man talar om är Workshop om fotbollens ekonomi och psykologi, och det mer fullständiga.programmet finns på EconPsyFootball06 - The University of Mannheim workshop on Economics and Psychology of Football (tyvärr hittades inga nedladdningsbara papers där).


Se även
Paric Andersson, Mattias Ekman, Jan Edman: Forecasting the fast and frugal way: performance and information-processing strategies of experts experts when predicting the World Cup 2002 in soccer (PDF)

DI.se: Experternas gissningar inte bättre än dina egna
DI.se: Ny studie från handelshögskolan dömer ut analytiker (2004-09-29)


Optimering av fotbollstittande som innehåller länkar till andra forskningsrön om fotbollsforskning.
Straffsparkar i fotboll och annan fotbollsmatematik


Andra bloggar om: , .

Posted by hakank at 05:53 EM Posted to Matematik | Sport, idrott, hälsa

juni 19, 2006

Lite nördmusikmotvideos

Eftersom jag inte tycker att Botten Anna-låten (knuff-länk) är speciellt bra (även om idén att förväxla en båt med en chatbot är skoj men det är en långsökt koppling och en väldigt dålig ordvits, (*)) så kommer här några motvideos:

* statz rapperz
* Finite Simple Group (of Order Two) (se vidare Klein Four Store).


(*) Association: Jag undrar hur Magrittes tavlor egentligen låter, och Dalis. Någon bara måste har tonsatt dem.


Andra bloggar om: , .

Posted by hakank at 07:04 EM Posted to Matematik | Comments (3)

juni 13, 2006

Mathematisk podcast: mathgrad podcast

Mathgrad Podcast är en sajt med podcastar kring vardagsmatematik, dvs mer eller mindre vardagsproblem sett ur matematiska ögon. Se exemplen nedan.

Målet med sändningarna beskrivs på följande sätt:


Welcome to the home of the Mathgrad Podcast where we discuss everyday math for everyday people. My goal is to discuss the mathematics behind many real life topics in a way that even the worst mathphobe will gain some insight.

Samt att fresta till vidare studier av matematik.

Här finns en lista över programmen. Det finns även Show notes, i skrivande stund endast för de fem första programmen.

Några exempel:
* Deal or no deal - Mathematics behind deal or no deal

* Moore's Law and Exponentials - Just how fast do things grow that grow exponentially

* Mathematics of Sharing - How can we divide things so that everyone is happy?

* Voting - Why the 2 party system? - We examine the mathematics of voting theory, learn some bad news about fair voting, and look at some specific and often used voting schemes.

* Maps and the lies they tell us - We explore the mathematics behind maps.


Jag har ännu inte lyssnat på alla programmen, men de jag hört har varit skoj.

Andra bloggar om: , .

Posted by hakank at 07:31 FM Posted to Matematik | Comments (4)

juni 08, 2006

Vilken boll är rundast? Slumpmässighet i sporter

I P1 pratades precis om att fotboll är den mest slumpmässiga sporten. Matematikern som intervjuades, Torbjörn Lundh, har skrivit Which ball is the roundest? – a suggested tournament stability index (PDF).

Abstract:


All sports have components of randomness that team not to win every game. According to many spectators of the charm when following a competition or a match. less of this unpredictability? We suggest here a general stability index, which could measure this randomness factor and different sports. As an illustration we use exemplify squash, and soccer. Results will also be given on tournaments football, ice-hockey, and handball. Furthermore, we will optimization questions that turned up on the way.

(Funnen via sidan Vetenskapsfestival 2006)

Uppdatering
Intervjun kan (förhoppningsvis) ålyssnas via följande djuplänk.

Malin på Vetenskapsnytt skrev i vintras (onsdag, januari 04, 2006) om en liknande undersökning: Fotboll är den mest spännande sporten, säger forskare, där följande paper omnämns:
E. Ben-Naim, F. Vazquez, S. Redner What is the most competitive sport? (arXiv.org)


We present an extensive statistical analysis of the results of all sports competitions in five major sports leagues in England and the United States. We characterize the parity among teams by the variance in the winning fraction from season-end standings data and quantify the predictability of games by the frequency of upsets from game results data. We introduce a mathematical model in which the underdog team wins with a fixed upset probability. This model quantitatively relates the parity among teams with the predictability of the games, and it can be used to estimate the upset frequency from standings data. We propose the likelihood of upsets as a measure of competitiveness.


Andra bloggar om: , .

Posted by hakank at 07:42 FM Posted to Matematik | Sport, idrott, hälsa | Statistik/data-analys | Comments (3)

april 22, 2006

Divisorträd: unika sätt att göra konsekutiva uppdelningar

Vilka - och hur många - unika sätt kan man göra följande "konsekutiva delningar" av ett antal saker. Tänk t.ex. på de olika unika sätt man kan dela upp N antal spelkort i olika högar. Metoden man arbetar med är följande:

- börja med en hög av N saker

- dela upp dessa saker i ett antal högar så att det är lika många saker i varje hög

- ta en av dessa högar och fortsätt på samma sätt tills det bara finns
en sak i varje hög

Eller på ett något mer matematiskt språk: på vilka - och hur många - olika unika sätt man kan dela upp ett tal i dess divisorer (förutom 1 och talet själv).

Not: Eftersom nedanstående inte har (matematiskt) bevisats så är det endast en hypotes (en förmodan).

Uppdatering. Hmm, jag har hittat en inkonsekvens i nedanstående. Inte bra. Återkommer...


Program: Divisor tree
Det program som används för att undersöka dessa konsekutiva delningar är Divisor tree / / Consecutive dealing in heaps. Nedanstående förklaringar är förhoppningsvis tillräckligt för att förklara programmet.

Notera att programmet endast arbetar med värden mellan 2 och (lite halv godtyckligt) 30000 av datorsnällhetsskäl.


Inledande exempel
Låt oss göra det mer åskådligt med 16 saker (t.ex. 16 spelkort).

För N = 16 finns det 4 olika sätt.


16 / 2 heaps = 8 things in each heap (2 -> 8 -> ..)
     8 / 2 heaps = 4 things in each heap (2 -> 4 -> ..)
         4 / 2 heaps = 2 things in each heap (2 -> 2 -> 1)
     8 / 4 heaps = 2 things in each heap (4 -> 2 -> 1)
16 / 4 heaps = 4 things in each heap (4 -> 4 -> ..)
     4 / 2 heaps = 2 things in each heap (2 -> 2 -> 1)
16 / 8 heaps = 2 things in each heap (8 -> 2 -> 1)

Found 4 ways for N = 16.

Beskrivning av det första (unika sättet):
* Först har vi 16 saker.
* Dessa delas upp i två högar med 8 saker i varje hög.
* Vi tar en av dessa två högar och har nu en hög med 8 saker. Denna delar vi upp i 2 högar så vi får 4 saker i varje hög.
* Vi tar en av dessa högar och delar upp i 2 högar med två saker i varje hög.
* Vi tar sedan en av dessa högar och delar ut i 2 högar med 1 sak i varje hög.

Men sedan kan vi inte gå vidare eftersom det nu är endast 1 sak i varje hög. Man skulle i och för sig kunna dela upp 1 sak i 1 hög i det oändliga men det är inte tillåtet i detta spel. Regel: När det endast finns 1 sak i en (färdigutdelad) hög är man klar med denna uppdelnin.

Antal saker som fanns i de högar vi använder under utdelningen är: 16, 8, 4, 2, (1).

Tittar vi på exempelkörningen ser vi att en unik väg (ett unikt sätt) är avslutat om raden avslutas med -> 1. Står det däremot -> .. så fortsätter uppdelningen och man går vidare till nästa (inskjutna) rad. Denna trädliknande struktur är anledningen till att det kallas för divisorsträd där de olika uppdelningssätten grenar ut sig. (Möjligen skulle det kunna kallas för divisorsstad eftersom det är vägar vi pratar om eller divisorsskog efterom det är flera träd med olika grenar, men ingendera av dessa känns lika naturligt som -träd).
De 4 olika sätten för N = 16 är följande, där talen anger antal saker i varje hög. Den första raden motsvarar alltså den långa beskrivningen ovan.

16 -> 8 -> 4 -> 2
16 -> 4 -> 2
16 -> 4 -> 2
16 -> 8 -> 2

För N=12 finns det 5 vägar (avslutas med 2 eller 3)

12 / 2 heaps = 6 things in each heap (2 -> 6 -> ..)
     6 / 2 heaps = 3 things in each heap (2 -> 3 -> 1)
     6 / 3 heaps = 2 things in each heap (3 -> 2 -> 1)
12 / 3 heaps = 4 things in each heap (3 -> 4 -> ..)
     4 / 2 heaps = 2 things in each heap (2 -> 2 -> 1)
12 / 4 heaps = 3 things in each heap (4 -> 3 -> 1)
12 / 6 heaps = 2 things in each heap (6 -> 2 -> 1)

Found 5 different way(s) for n = 12.


Primtal
Om det finns ett primtal antal saker i en hög finns det endast ett sätt (en väg) att dela upp i lika antal högar, nämligen att dela så att det finns en sak i varje hög. T.ex. om man har 13 kort så kan man endast dela ut dem i 13 olika högar med 1 kort i varje hög.

En väg avslutas alltså om det blir en hög innehåller primtal stycken saker. Eller mer korrekt: Om det är primtal antal stycken blir nästa uppdelning så många högar med 1 sak i varje hög.


Primtalskvadrater
För 4 saker så finns det bara ett sätt: nämligen att dela upp i två högar med två saker i vardera.

4 / 2 heaps = 2 things in each heap (2 -> 2 -> 1)

Found 1 different way(s) for n = 4.

Detta är ingen slump. För varje kvadrat av primtal (2^2=4, 3^2=9, 5^2=25, 7^2=49 osv) så finns det endast ett sätta att göra uppdelningen.

Båda dessa specialfall, primtal och primtalskvadrater utnyttjas i den rekursiva algoritm för att räkna ut antalet unika konsekutiva uppdelningar, och som beskrivs nedan.


Antal uppdelningar, heltalssekvenser
Om man nu räknar antalet unika sätt att göra denna typ av uppdelningar för N = 1.. 32 får vi följande heltalssekvens:


1,1,1,1,1,2,1,2,1,2,1,5,1,2,2,4,1,5,1,5,2,2,1,12,1,2,2,5,1,9,1,8

Här är en graf över sekvensen för N = 1 .. 512:

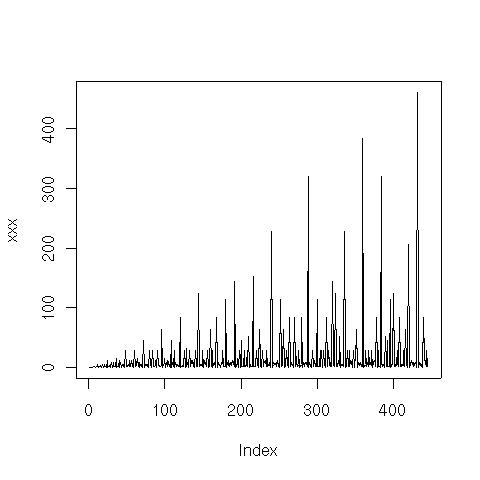
Ett bra sätt att analysera denna typ av matematiska (eller algoritmiska) strukturer är att se om det finns andra strukturer som har samma heltalssekvens. Det gör man lämpligen via On-Line Encyclopedia of Integer Sequences (som beskrivits tidigare i Heltalssekvenser). Ovanstående sekvens fanns inte med! Inte heller hittades sekvensen via superseeker som är en tjänst där man mailar in sekvensen och där systemet gör väldigt många olika typer av transformationer av sekvensen. Inte heller där hittades sekvensen.

Så det verkar som om ovanstående sekvens är ganska ovanlig. Lite märkligt eftersom det känns som en "naturlig" metod. Vi ser nedan att det är en "kusin" till en känd heltalssekvens.


Rekursiv definition
Ovanstående sekvens räknades ursprungligen ut genom att skapa vägarna i en tidig version av programmet Divisor tree, men sedan skapades (upptäcktes) en metod för att räkna ut dessa värden mycket enklare. Här är pseudokoden för metoden:


divtree(n):
   # n > 0
   if n == 1 then value = 1 # specialfall för n = 1
   elsif prime(n) then value = 1 # primtal
   else if prime_square(n) then value = 1 # kvadrat av ett primtal
   else if # annars: loop igenom divisorerna av n
     for div = divisors(n) do
     next if div == 1 or div == n # se kommentaren nedan
     value = value + divtree(div) # summera divisorernas värden rekursivt

   return value

Notera raden med "next" i for-loopen. Den innebär att om divisorn är 1 eller n så adderar man inte något värde för denna divisor. (Det är genom att förändra next-raden som vi hittar sekvensens kusin. Se nedan) Notera också att det är en rekursiv definition.

Pratversionen av metoden är ungefär: Om N är 1, ett primtal eller en primtalskvadrat så finns det ett unikt sätt att göra en delning. Om N är något annat så summerar man divtree-värdena för N:s divisorer (alla divisorer förutom 1 och N själv).

Det tarvar kanske ett exempel på detta, så låt oss titta på N = 24 (dvs 24 saker). Först divisorsträdet:

24 / 2 heaps = 12 things in each heap (2 -> 12 -> ..)
     12 / 2 heaps = 6 things in each heap (2 -> 6 -> ..)
         6 / 2 heaps = 3 things in each heap (2

Posted by hakank at 11:09 FM Posted to Matematik | Program | Comments (2)

april 19, 2006

de Bruijn-sekvenser av godtycklig längd

För några år sedan skrevs ett program för att skapa de Bruijn-sekvenser, som kortfattat kan förklaras som en sträng (cykel) som innehåller ("testar") alla förekomster av delsträngar, där delsträngarna är representationer av tal. Mer förklaringar och exempel ges i de Bruijn-sekvenser (portkodsproblemet) och programmet de Bruijn sequence. I slutet finns även några andra referenser.

De metod som dessa sekvenser konstrueras ger endast stränglängder med jämna potenser, dvs 2^2 = 3, 2^3 = 8, 3^2 = 9, 3^3 = 27 osv. En fråga som ställdes tidigt var: Kan man skapa sådana sekvenser för en godtycklig längd, t.ex. 11, 17 eller 52 och för godtycklig bas, 2, 6,11 etc? Basen är alltså den kodning av talen man använder, där.basen 2 ger en binär representation (0,1), basen 3 använder 0, 1,2 osv.

Svaret på frågan är: Visst kan man det!

Än så länge har jag dock inte kommit på en vacker algoritm som den som finns för "vanliga" de Bruijn-sekvenser. Se The (Combinatorial) Object Server, Information on necklaces, unlabelled necklaces, Lyndon words, De Bruijn sequences (i slutet på sidan finns det länkar för att ladda ner källkod).


Programmet "de Bruijn arbitrary sequences"
Programmet de Bruijn arbitrary sequences visar några av resultaten av denna undersökning. Troligen behövs lite förklaringar av programmets metoder och parametrar och sådant bistår jag så gärna med.


Metoden: slumpa cykler
Principen för att skapa dessa sekvenser är enkel: Skapa en de Bruijn-graf och slumpa fram cykler i denna graf tills en av korrekt längd hittas.

Denna slumpmässighet är det som gör att programmet inte tillåts arbeta med speciellt stora värden.


de Bruijn graf
En de Bruijn-graf är en graf där kopplingarna mellan talen (noderna) följer "de Bruijn-regeln" att ett tals suffix ska vara ett annat tals prefix i deras *-ära representation. T.ex. det binära talet 000 kan kopplas till 001, talet 001 med 010 och 011 osv. Baser större än 2 hanteras på motsvarande sätt.

Exempel: Här visas kopplingarna i grafen för n = 16 i basen 2. Inom parentes visas den binära representation av talet.

0: 0 1 (0000)
1: 2 3 (0001)
2: 4 5 (0010)
3: 6 7 (0011)
4: 8 9 (0100)
5: 10 11 (0101)
6: 12 13 (0110)
7: 14 15 (0111)
8: 0 1 (1000)
9: 2 3 (1001)
10: 4 5 (1010)
11: 6 7 (1011)
12: 8 9 (1100)
13: 10 11 (1101)
14: 12 13 (1110)
15: 14 15 (1111)

Här är en mer grafisk representation (skapat med programmet dot).
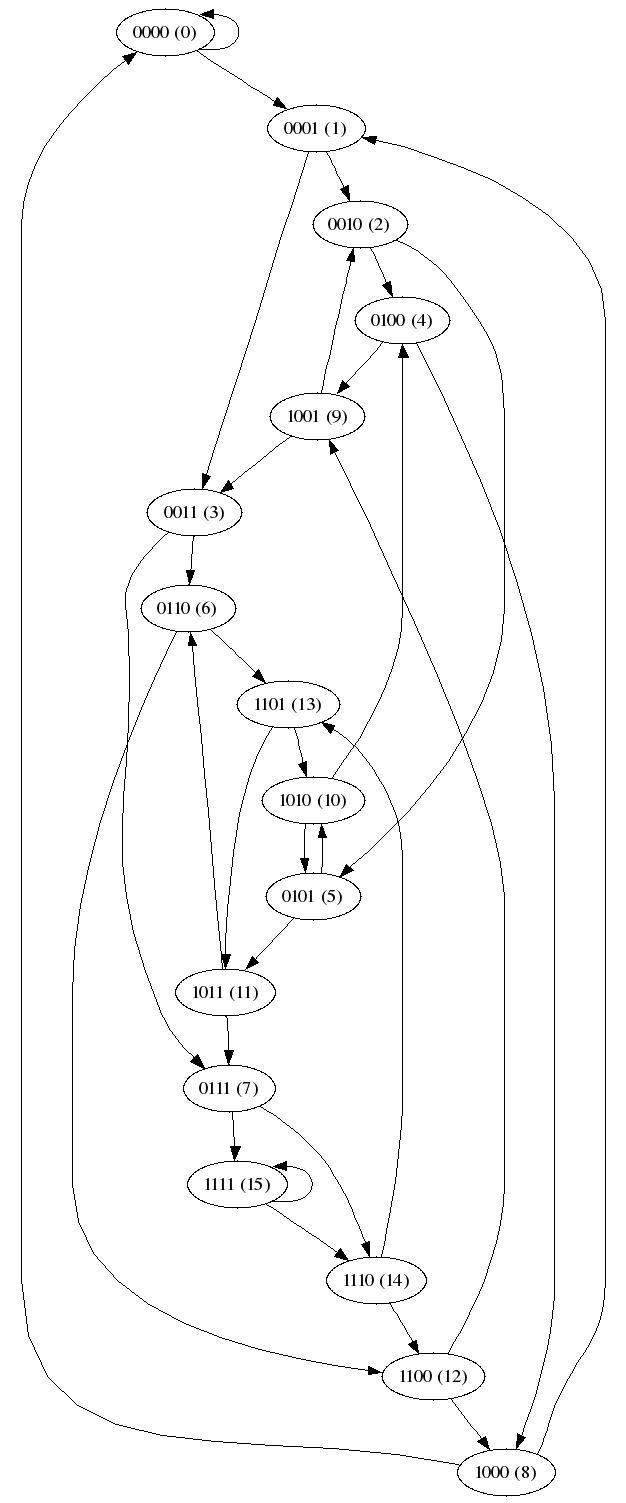(klicka på bilden för att förstora den).


Antalet noder
Antalet noder i de Bruijn-grafen räknas ut enligt följande (motsvarar nearest_power i pseudo-koden nedan):
- om n är en jämn potens för basen används n noder (talen 0..n-1). T.ex. n=16 bas 2 är 2^3 är en sådan jämn potens.
- annars är antalet noder den närmaste efterföljande jämna potensen för basen. Exempel: För n=7 (bas 2) blir det 8 noder (2^3=8 ). För n=21 bas 3 blir det 27 noder (3^3=27 ) osv.

Kopplingsgrafen är enkel att räkna ut och principen ses nog vid närmare granskning av några exempel. Hur som helst kommer här pseudo-kod:


# nearest power in the choosen base, or N itself if N is a power
next_pow = nearest_power(N, base)
half_pow = next_pow / base;

for num (0..next_pow-1) {
   for b (0..base-1) {
     x = base * (num % half_pow);
     conn = x + b;
     graph->add_edge(num, conn); # connect num -> conn
   }
}


Kort förklaring av programmet
Programmet har en del parametrar vilka här förklaras.

N (2..64): Det är stränglängden (eller antal objekt). Kan vara mellan 2 och 64.

Base (2..4): Basen som ska användas. T.ex. för bas 2 är det binär representation (0,1). Giltiga värden är 2,3 eller 4.

Type: normal / reversed: Normal innebär att sekvensen visas normalt från vänster till höger och de binära (bas-ära) talen kodas normal (7 binärt är "0111"). Det lägsta talet börjar decimalcykeln. Reversed är då man vänster på allting: de binära (etc) koderna är omvända (7 visas som "1110") och det högsta talet i decimalcykeln visas först.

Show connections: Visar kopplingarna för den de Bruijn-graf som byggs upp.

Show sequence: Här visas de individuella representationerna.


Exempel
Här är ett exempel på på en av många möljiga sekvenser för n = 52 i basen 4:

Sequence:0001012131301132230220330300323123212013332002102331

Cycle (in decimal): 0 1 4 17 6 25 39 29 55 28 49 5 23 30 58 43 44 50 10 40 35 15 60 51 12 48 3 14 59 45 54 27 46 57 38 24 33 7 31 63 62 56 32 2 9 36 18 11 47 61 52 16

Sequence check:

000101213130113223022033030032312321201333200210233100
000 (0)
 001 (1)
  010 (4)
   101 (17)
    012 (6)
....


Begränsningar
Som ovan nämnts bygger programmet på en slumpning av cyklerna. Det kan ta en stund att slumpa fram cykler av korrekt längd i stora grafer så finns det några begränsningar för att datorn inte ska bli sönderkörd:

N: mellan 2 och 64
base: mellan 2 och 4

Om någon läsare nu (eller sedan) upplever ett starkt behov av sådana sekvenser med större längd / bas så är det bara att kontakta mig (hakank@bonetmail.com så kan vi säkert ordna något.


Vidare utveckling
Denna slumpmässiga metod fungerar om det är relativt små värden av N och bas. Men för större värden är det inte en tillgänglig metod. I stället bör en deterministisk algorim skapas.

Ett pågående projekt är också att försöka minska antalet noder i grafen så att det inte blir så många möjliga cykler att leta igenom.


Not
Jag är osäker på om ovanstående fortfarande kan kallas för en de Bruijn-sekvens när man använder denna alternativa approach.


Se även
de Bruijn sequence (den "vanliga" formen)
de Bruijn-sekvenser (portkodsproblemet)

MathWorld deBruijnSequence
COS: Information on necklaces, unlabelled necklaces, Lyndon words, De Bruijn sequences

Posted by hakank at 06:52 EM Posted to Matematik | Program

april 18, 2006

Choco: Constraint Programming i Java

Bakgrund
Mitt intresse för Constraint Programming (CP) (som tidigare kallades Constraint Logic Programming, CLP) väcktes för ett antal år sedan strax efter en företagskamp (som kort beskrevs i Uppdaterat program: AnaCheck), där ett av uppdragen var följande matematiska pyssel:

Vilken är den minsta differensen man kan få mellan två tal om man måste använda samtliga siffror (0..9) exakt en gång?

Lösningen presenteras nedan.

Ungefär samtidigt stötte jag på Constraint (Logic) Programming och med detta och liknande pyssel i bakhuvudet, och blev väldigt fascinerad av programmeringsparadigmet. Kanske inte så förvånande eftersom många standardexempel är just matematiska pyssel.

Tanken är att man endast behöver skriva de problemspecifika villkoren (constraints), sedan får systemet lista ut bästa sättet att lösa problemet. Det finns många olika metoder och heuristiker för att lösa problemen, och ibland måste hjälpa till så att lösningen kommer denna sidan regnbågen eftersom vissa problem är mycket tunga.

Ett citat som ofta nämns i sammanhanget är Eugene C. Freuder (CONSTRAINTS, April 1997)


Constraint programming represents one of the closest approaches computer science has yet made to the Holy Grail of programming: the user states the problem, the computer solves it..


Prologbaserade system
I början arbetade jag mestadels med logikprogramspråket Prolog som "moderspråk", Sicstus Prolog samt ECLiPSe Constraint Programming System (det senare inte att förväxlas med utvecklingsmiljön med ungefär samma stavning).


Imperativa språk
Som komplement till de Prologbaserade systemen har jag letat efter mer imperativa - samt icke-kommersiella - moderspråk såsom Java, C, C++, Perl, Python, eftersom vissa saker är lättare att programmera med sådana språk (men ibland svårare) En av dessa implementationer Python-constraint och nämns i kommentarerna till Sesemans matematiska klosterproblem samt lite Constraint Logic Programming.


Choco
Så till det system jag har kollat i nyligen: det Java-baserade Choco. I slutet av anteckningen finns fler referenser.

Choco är snabbt och det har en stor mängd funktioner. Exemplen nedan är endast för "finita domäner" (löses med hjälp av heltal), men det finns även domäner med reella tal samt mängder.

Det är dock inte lika elegant att skriva constraints som i Sicstus/ECLiPSe, vilket vi nu kommer att titta på.


Minsta differensproblemet - en jämförelse av kodskrivning
För att tydliggöra skillnader och likheter mellan Choco och de Prologbaserade systemen visas hur minsta differensproblemet kan lösas i respektive system.

I ECLiPSe skriver man själva constraint-delen av problemet på följande sätt; i Sicstus Prolog skriver man snarlikt. Obs: koden är inte riktigt komplett att bara köra.

:-lib(fd), lib(fd_search), lib(fd_global),lib(fd_domain).

% ....

LD = [A,B,C,D,E,F,G,H,I,J], % deklarera de 10 variablerna
LD :: [0..9], % intervallet för variblerna, mellan 0 och 9
fd_global:alldifferent(LD), % alla värden ska vara olika

%
% constraints
%

% A + B + C + D + E = F + G + H + I + J
X #= 10000*A+1000*B+100*C+10*D+E,
Y #= 10000*F+1000*G+100*H+10*I+J,

% differensen ska bli positiv
X #< Y,

% differensen
Diff #= Y - X,

% minimera differensen (Diff) samt heuristik för att hitta lösningen snabbt
minimize(search(LD,0,anti_first_fail,indomain_max,credit(64,bbs(15)),[]),Diff).

Elegant och lite magiskt, eller hur?

Motsvarande Choco-program är lite längre, främst eftersom det saknas syntaktiskt socker. Det går att pressa antalet rader (sådant har gjorts) men här görs en mer expressiv form för att jämförelsen ska bli tydligare. Programmet finns att ladda ner här nedan.


// Choco program

import choco.Problem;
import choco.*;
import choco.integer.*;

public class LeastDiff {

public static void main(String[] args) {
new LeastDiff().puzzle();
}

public void puzzle () {
Problem pb = new Problem();

// definiera variablerna A .. J så att dess värden är mellan 0 och 9
IntDomainVar A = pb.makeEnumIntVar("A", 0, 9);
IntDomainVar B = pb.makeEnumIntVar("B", 0, 9);
IntDomainVar C = pb.makeEnumIntVar("C", 0, 9);
IntDomainVar D = pb.makeEnumIntVar("D", 0, 9);
IntDomainVar E = pb.makeEnumIntVar("E", 0, 9);
IntDomainVar F = pb.makeEnumIntVar("F", 0, 9);
IntDomainVar G = pb.makeEnumIntVar("G", 0, 9);
IntDomainVar H = pb.makeEnumIntVar("H", 0, 9);
IntDomainVar I = pb.makeEnumIntVar("I", 0, 9);
IntDomainVar J = pb.makeEnumIntVar("J", 0, 9);

IntDomainVar[] letters = {A,B,C,D,E,F,G,H,I,J};

IntDomainVar Diff = pb.makeBoundIntVar("Diff", 0, 10000);

// Temporära variabler
IntDomainVar X = pb.makeBoundIntVar("X", 0, 100000);
IntDomainVar Y = pb.makeBoundIntVar("Y", 0, 100000);

// alla värden ska vara unika
for (int i = 1; i <= 9; i++) {
for (int j = 0; j <= 9; j++) {
if (i==j) {
continue;
}
pb.post(pb.neq(letters[i], letters[j]));
}
}

// X = A+B+C+D+E
pb.post(pb.eq(X, pb.scalar(new int[]{10000, 1000, 100, 10, 1},
new IntDomainVar[]{A,B,C,D,E})));

// Y = F +G + H + I + J
pb.post(pb.eq(Y, pb.scalar(new int[]{10000, 1000, 100, 10, 1},
new IntDomainVar[]{F,G,H,I,J})));

// Diff = X - Y
pb.post(pb.eq(pb.minus(X, Y), Diff));

// minimera skillnaden
pb.minimize(Diff,false);

// nu ska vi lösa problemet
Solver s = pb.getSolver();
pb.solve(true);

// Skriv ut lösningen
System.out.println("Result: "+ A.getVal() + B.getVal() + C.getVal() +D.getVal() + E.getVal() + " - " + F.getVal() + G.getVal() + H.getVal() + I.getVal() + J.getVal() + " = " + Diff.getVal() );

} // end puzzle

} // end class


Lösningen som ges av dessa båda program är samma, nämligen

50123 - 49876 = 247


Några körbara (kompilerbara) Choco-program
Här är källkoden till några andra mindre Choco-program, varav några är standardproblem inom constraint programming. Choco-distributionen innehåller några andra.

LeastDiff2.java: Ovanstående exempel
FurnitureMoving.java: Planering av möbelflyttande, använder cumulative.
Knapsack.java: ett enkelt knapsack-problem (minimize)
Zebra.java: ett standardpyssel
Seseman.java: Choco-versionen av Sesemans matematiska klosterproblem


Se även
om Choco:
Choco: projektsidan på Sourceforge
Wiki
User guide
Choco API
Forum

om constraint programming
Roman Barták: On-line Guide to Constraint Programming
Roman Barták: Constraint Programming: In Pursuit of the Holy Grail (PDF)


tidigare skrivet om C(L)P
Sesemans matematiska klosterproblem samt lite Constraint Logic Programming
Automatisk "lösning" av Minesweeper i Mozart/Oz


JaCoP är ett annat Javabaserat system, utvecklat vid Lunds Universitet som man kan få tillgång till om man frågor någon av dess skapare. Har inte kollat in det så mycket ännu, men det verkar också trevligt.

Posted by hakank at 09:59 EM Posted to Constraint Programming | Matematik | Pyssel

mars 05, 2006

Ivars Peterson blogg Math Trek (nöjesmatematik)

En av mina stora favoriter inom nöjesmatematiken (recreational mathematics) är Ivars Peterson. För ett tag sedan begåvades han med en blogg: MathTrek. Det är troligen inget slump att det råkar vara samma namn som dennes matematikkolumn.


Se även
Math Trek archives .
MatheMUSEments: Articles about math in everyday life.
Bokussökning: Ivars Peterson.

Rekreationell matematik ocn annat tankegodis

Posted by hakank at 09:06 FM Posted to Matematik

november 21, 2005

Bloggforum 3 - Några tankar samt Isobels och Lisas pizzeriabordsproblem

Nedanstående är inte avsedd att vara någon fullständig redovisning av vad som hände eller gjordes under Bloggforum 3 eller helgen kringgärdande detta evenemang. Snarare är det tankar kring det man pratade om i och utanför det formella programmet. Vad gäller fysiska trajektorier och de yttre omständigheterna kan refereras till Mats Anderssons utmärkta och innehållsrika Summering av Bloggforum 3.

Ett stort tack till Rebecca Crusoe, Stefan Geens och Erik Stattin för deras fina arbete att anordna ett så intressant program, och som gjorde det möjligt att få förmånen träffa så väldigt trevliga och intressanta personer.

Det har skrivit väldigt mycket redan om forumet. De naturliga samlingspunkterna är
- Bloggforum 3
- del.icio.us/tag/bloggforum3

Bloggen är död
Temat (med glimten i ögat) för detta forum var "Bloggen är död". Det är egentligen absurt att nu när begreppet blogg håller på att bli känt för en större allmänhet anser man att bloggen är död.

Personligen har jag sedan ett tag känt att formatet känts begränsande i vissa fall. I såväl bloggverktyg som kommentarer finns en tendens att endast bry sig om det som skrevs nyligen. Det innebär att det man skrivits tidigare (t.ex. en vecka, en månad eller ett år sedan) inte läses längre i ett naturligt sammanhang. Denna dominans till det kronologiska har alltså stört mig rätt länge. I vissa fall är det naturligt eftersom det ofta är dagsaktuella frågor som diskuteras och man anser att debatt etc är över. Men det man missar är samlandet av kunskap kring det som man - eventuellt - kom fram till.

Det verkar även finnas andra som haft liknande tankar kring begränsningarna, men kanske av andra skäl, vilket inte är så konstigt. Nu har man hunnit experimenterat med mediet, funnit det som passar ens egna syften och identifierat det som är mindre intressant. Det verkar gälla såväl traditionell (text)bloggning, podcasting som videobloggning. Detta är tiden att fundera över mediers inneboende begränsningar.

Stefan Geens undrar lite Bloggforum 3 - what I saw vad Bloggforum 4bör innehålla. Det rykte som Jon skriver om i sin kommentar är något som bl.a. jag själv underblåst (eller vad det nu är man gör med rykten), eftersom jag inte tror att det finns behov för ett Blogg-forum om ett halvår, och diskuterade detta lite med både Erik Stattin och Stefan Geens i helgen.

Däremot ser jag mycket fram emot ett X-forum (alternativt X-logg-forum) där man visar hur det-vi-nu-nu-kallar-blogg ("the thing formerly known as blog") har utvecklats och förändrats, och hur det eventuellt påverkat t.ex. socialt eller tekniskt. Självklart kommer det fortfarande att finnas bloggar med eller utan t.ex. wiki-liknande utökningar, men jag tror och hoppas att vi kommer att se en större variantion i såväl form som innehåll.

Troligen har det om ett halvår även hänt saker inom lagstiftning, politik, media samt i det sociala landskapet (t.ex. olika typer av forskning kring bloggning) som är väl värt att föreläsa om eller ha sessioner kring.

Som Ben Hammersley beskriver i sin "Åtta idéer som verkligen kommer att revolutionera 2000-talet (och varför blogging inte är en av dem)" är bloggen i sig inte inte en någon revolutionerande idé, men inkorporerar många av de idéer som har eller kommer att revolutionerna informationsamhället eller åtminstone påverka det.


Web 2.0 och agenter
Under flera tillfällen diskuterades det Web 2.0, t.ex. med Simon Winter, Henrik Torstensson och Jon Åslund. Jag har inte stenkoll på vad det är och tycker det liknar det som man sa kring 98/99 om webben eller t.ex. när WAP kom. Men nu har det faktiskt blivit möjligt för en företagsam person att göra dessa applikationer med öppna API och "öppen data".

En sak som jag har saknat i diskussionerna är intelligeta agenter som kommunicerade med varandra för att lösa all världen (informations)problem. Vad blev de egentligen av? Jag vill ha min shoppingagent!


Jyri Engström: Sociala object
Jyri Engströms föredrag var det föredrag som jag var mest intresserad av och var även det som jag uppskattade mest. Engström poängterade att det viktiga med sociala mjukvaroprogram (och man borde kunna se bloggen som ett sådant) är gemensamma sociala objekt, där objekt kan vara väl definierat men även uppstå spontant efter ett tag.

Som exempel på hur viktigt det är med gemensamt socialt objekt visades en av mina favoriter bland Monty Python-sketcherna: Fotbollsmatchen mellan grekiska och tyska filosofer. Detta fick mig att parafrasera Wittgensteins berömda setens från Filosofiska undersökningar: "a serious and good philosophical or social work could be written that would consist entirely of jokes from Monty Python".

Inledningsvis nämnde Engström några böcker som jag har faktiskt läst och skrivit lite om, se mer Social Network Analysis och Complex Networks - En liten introduktion. Se även tidigare bloggningar: Social Network Analysis/Complex networks.

Engström rekommenderade även en nyutkommen bok (den där med bilderna på det italienska mötet respektive potatisodlingen) och som verkar intressant: John Thackara In The Bubble - Designing in a Complex World.

Det antyds att Lotta at Work kommer att publicera ljud/video från Engströms föredrag.


Ben Hammersleys vision
Ben Hammersley hade en något provocerande rubrik på sitt föredrag "Åtta idéer som verkligen kommer att revolutionera 2000-talet (och varför blogging inte är en av dem)" som fick sin förklaring, och gav faktiskt en koppling till bloggandet genom att bloggande (och bloggare) "inkorporerar" alla(?) dessa punkter.

Föredraget var intressant även om jag inte riktigt håller med honom i hans undergångsbeskrivning. Hans tes att detta är en unik tid som vi aldrig tidigare skådat känns också som en något omotiverad kontemporär-centrism, dvs att vår tid är viktigare eller mer märkvärdigt än tidigare tider. Vad är det för märkvärdigt med vår tid? Å andra sidan är uppgång och nedgång av civilisationer inte heller någon naturlag.


En kommentar kring en detalj som verkar vara viktigt för resonemanget. Hammersley menar att den tekniska utvecklingen numera bara fortsätter att öka genom att den tekniska utvecklingen förstärker sig själv, t.ex. genom att snabbare datorer gör det möjligt att skapa ännu snabbare datorer som i sin tur möjliggör skapande av snabbare datorer etc. Han stödde denna tes med en bild föreställande en exponentiell kurva som påstods visa att datorerna blir allt snabbare/billigare/kraftfullare datorerna utan någon gräns eller avtagande. Troligen kan man även tolka kurvan som en logistisk kurva, eftersom den i början ser den ut som en exponentiell kurva men planar sedan ut till en "mättnadsnivå". En alternativt tolkning att det var i stort sett samma kurva ("sinuskurva") som Hammersley tidigare visat att symboliserade tidigare civilisationer hade följt: först uppgång, sedan nedgång ("crawling in the mud"?) och sedan uppgång igen och sedan nedgång. Således är det inte nödvändigt att det är en exponentiell tillväxt.

Han varnade i och för sig för att beskrivningen skulle störa personer med vissa kunsaper inom historia och teknik (samt eventuellt matematik).

Hur som helst var det ett mycket energirikt och inspirerande föredrag. Det finns en ljudupptagning via Lotta at Work.


Mozz Hussain: MSN Spaces i praktiken
Mozz Hussain "Busting blogging myths - the present and future of blogging" handlade om erfarenheterna kring MSN Spaces. Det var i och för sig intressant och gav inblickar i den sociala strukturen kring bloggar, men detaljerna fastnade inte så mycket. Kanske beror detta på att MSN Spaces inte representerar så mycket den typ av bloggning som jag själv tycker är mest intressant att följa, det som bl.a. Jonas Söderström kallar för kunskapsbloggar.


Copyfight
Detta hade jag sett framemot, bl.a. eftersom Simon Winter var med i panelen. Simon är en av mina absoluta favoriter bland de svenska bloggarna och som jag haft förmånen att träffa flera gånger tidigare. Simon summerar några av sina tankar kring debatten i Vad är viktigt med upphovsrätt?.

Med en något elak förenkling kan man säga att man kom fram till att man egentligen inte vet vad som gäller. Det var dock intressant att följa debatten, speciellt de konkreta exemplen som framfördes såväl från panelen som publiken.

Debatten blir inte lättare med att begreppen "kopiering", "fildelning", "piratkopiering" nu är så inflammerade att det verkar som en vettig diskussion av det är omöjlig, och det känns som om antipiratbyrå-sidan för tillfället äger dessa begrepp. Ett förslag är att försöka hitta en mer neutral begreppsapparat som gör det möjligt att föra rationella diskussioner. Under kvällen föreslogs det att begreppet "kopiera filer" skulle bytas ut mot det neutrala "kgegg" (så tror jag att det stavas), ett ord som länge sökt sin användning.


Gamla vänner, nya vänner samt att bli överraskad
Waldemar på Teche skriver följande i Det bloggforum jag inte var på:

Jag är lite förvånad över bloggosfären fortfarande håller i sig som en enad miljö. Trots allt är det ju rätt skilda ämnen och åsikter som avhandlas numer, men att man ännu delar en gemensam plattform... det tyder på att det kanske kommer att hålla i sig.

Ett skäl till kan exemplifieras med just Bloggforum är just att där finns så många olika intressen men alla har en gemensam referensram: bloggar. De allra flesta är också sådana som brinner för något och sådana personer är nästan alltid intressant att träffa eller få kontakt med (undantag finns naturligtvis). Det är flera kluster som - speciellt i Bloggforum - blandas i det gemensamt intresse av att uttrycka sig . I pausar, lunchen eller på "cocktail-partyt" kan man mingla med personer som man normalt inte träffar. Precis som i riktiga vänskapslivet kan man bli "hit it off" med en väns vän eller dennes vän

Den sociala poängen med dessa tillställningar är flerfaldig: att träffa sina gamla vänner, att prata med dem man har läst men inte träffats tidigare, samt helt enkelt bli överraskad av ett möte med någon man inte ens kände till. Detta sistnämnda ska inte underskattas.

På ungefär samma sätt vill man att sociala nätverkssystem ska fungera. Nyhetsbevakningsystem och rekommendationssystem har liknande syften:
- man vill bli uppdaterad inom de områden man känner väl till
- man vill lära sig mer inom ett ämne
- man vill bli överraskad av nya kunskaper eller ämnen.


En social nätverksanalys-kommentar: I många Bloggforum 3.0-redogörelser länkas det till personerna som träffats. Det skulle vara intressant att jämföra dessa med t.ex. bloggrullen eller de man länkat till föregående samt eventuellt efterföljande. Avspeglar kontakterna på Bloggforum det normala sociala mönstret inom bloggosfären? Min egen intuition kring detta är att cocktail-parties har en annan social dynamik än de dagliga bloggkontakterna.


Några längre-än-kortare kontakter
Här är den nästan-obligatoriska lista över personer som träffades och som pratades med mer än några sekunder. De med (*) anger nya IRL-bekantskaper. Det skulle ta alldeles för lång tid att skriva ner vad vi pratade om så det blir i stort sett endast en uppräkning av namn. Tack till er för trevliga pratstunder.

- Mats Andersson, resekamrat, hotellrumssdelare, gåtlösare samt galapetter
- Steffanie Müller
- Simon Winter
- Stefan Geens
- Andreas Haugstrup (*)
- Henrik Torstensson
- Någonting Söderström(?), Henrik Torstenssons ej bloggande kompis (*).
- Eric Wahlforss (*)
- Erik Stattin
- Jenny Isaksson (*)
- Niki Bergman (*)
- Rebecca Crusoe
- Daniel Lundh (*)
- Håkan Hakke Karlsson, varvid våra respektive skulder tillvarandra nu är reglerade.
- Rosemari Södergren (*)
- Erik Starck
- Jimmy Wilhelmsson
- Johnny Söderberg, mitt mål att prata med honom mer än några sekunder blev uppfyllt.
- David Hall
- Lisa Förare Winbladh
- Isobel Hadley-Kamptz (*), naturen av vår kontakt beskrivs nedan under "Isobels och Lisas pizzeriabordsproblem".
- Jonas Söderström
- Jon Åslund (*)
- Coola morsan, men vi hade lämnat vår musikideologiska skiljelinjer bakom oss.
- Oscar Swartz (*)
- Karolina Lassbo (*).
- Per Gudmundsson


Två personer som jag inte träffade men hade tänkt prata med:
- Patrik Wallström (som jag skulle hälsa från en gemensam vän tillika listsvågrar)
- Christian Ubbesson (listsvåger och arbetar med saker, text mining, som jag är intresserad av)


Geekighet
Jag var med i flera diskussioner om geeekighet, vilket nog faller sig naturligt på en så här rätt geekig tillställning. Många av de personer som jag pratade med eller åhörde kan nog anses vara geekar, i alla fall i en något vidare mening (se nedan).

* en mer allmän diskussion med Steffanie Müller som började med att hon ansåg mig vara en större geek än hon själv (som om man kan jämföra geekigheter på detta sätt), varpå vi diskuterade naturen av detta begrepp.

* Jimmy Wilhelmsson berättade om dokusåpan FCZ som består av ett gäng geekar som spelar fotboll (och som jag inte sett men ändå stött på indirekt i ett rätt geekigt sammanhang) där geeken nu får ett ansikte och personlighet.

* både direkt och indirekt med Jon Åslund - som jag uppfattar som en übergeek, och det är en komplimang, Jon - i alla fall de facetter jag såg, vilket möjligen avspeglar mina egna intressen och värderingar. Lite roligt här är att jag förra söndagen stötte på Jons namn i ett helt annat sammanhang; nästan helt annat, eftersom det var i samband med att Hakke lämnade in sina svar på Bloggforum-pyssel i lite för poetiska formuleringar, nämligen att Jon är skapare av det underbara programspråket The Shakespeare Programming Language som jag känt till tidigare.

Det finns ett test The Nerd? Geek? or Dork? Test där jag själv fick följande resultat:


Pure Nerd
82 % Nerd, 47% Geek, 43% Dork
For The Record:

Man definierar de olika begreppen på ett sätt som jag inte nödvändigtvis håller med om.


A Nerd is someone who is passionate about learning/being smart/academia.
A Geek is someone who is passionate about some particular area or subject, often an obscure or difficult one.
A Dork is someone who has difficulty with common social expectations/interactions.

You scored better than half in Nerd, earning you the title of: Pure Nerd.

The times, they are a-changing. It used to be that being exceptionally smart led to bei
ng unpopular, which would ultimately lead to picking up all of the traits and tendences
associated with the "dork." No-longer. Being smart isn't as socially crippling as it o
nce was, and even more so as you get older: eventually being a Pure Nerd will likely be
replaced with the following label: Purely Successful.

Isobels och Lisas pizzeriabordsproblem
Under lunchen satt vi (Lisa, Rosmarie, Johnny, Hakke, hakank samt Daniel) på en pizzeria. Efter en stund ropar Lisa: "Isobel!" varpå denna kom fram till vårt bord. Efter lite inledandes flamsande ville naturligtvis Isobel och Lisa uttrycka sin ömsesidiga vänskap genom en kram eller liknande, varvid man insåg snabbt att ett logistiskt problem hade uppstått genom att bordplaceringen var sålunda:

Förkortningar:
1: Lisa (som alltså är den som känner Isobel)
2: Rosmarie
3: Johnny
4: Hakke
5: hakank
6: Daniel

Bordplaceringen:
_ V Ä G G
V 2 4 6
Ä _ _ _ Isobel (stående och rörlig)
G 1 3 5
G
_ V Ä G G

Där "V Ä G G" - på härsan och tvärsan - betyder omgärdande av en vägg eller väggliknande hinder. Bordet motsvaras av "_ _ _".


Problem: Hur optimerar man en hälsningsceremoni mellan Lisa och Isobel?
Eftersom sällskapet omslutes av tre väggar (eller väggliknande hinder) finns det inget sätt sätt för Isobel och 1 att enkelt uttrycka en fysisk hälsningsceremoni utan att 3 och 5 förflyttar sig från soffan. Det fanns ingen plats under bordet för Isobel att krypa in under, och det var såväl fysiskt, ekonomiskt som socialt omöjligt att använda bordet som transportsträcka. (Alternativa lösningar som att använda en wire för att utnyttja det lediga luftrummet ansågs inte realistiskt eftersom vi skulle alla vara tillbaka inom rätt kort tid och kranarbetarna var troligen på lunch under denna tid. Att använda elektronisk utrustning för att t.ex. skicka hälsningsemail, hälsnings-SMS eller bloggogram tänkte man troligen inte på i den då innevarande stunden.)


Lösningsalternativ A
Följande lösning är troligen det normala förfarandet i liknande uppkomna situationer. Inom parentes anges kostnaden för förflyttningen (se även kommentaren nedan), där vi här antar att förflyttning av en plats kostar 1 (dvs en enhet något).

a) Isobel flyttar sig en liten bit ut från bordet för att ge plats åt 5 (1)
b) 5 makar sig ut från bordet (1)
c) 3 makar sig ut från bordet (2)
d) 1 makar sig ut från bordet (3)
e) 1 uttrycker sin vänskap med Isobel (0)
f) 1 makar sig tillbaka till sin plats (3)
g) 3 makar sig tillbaka till sin plats (2)
h) 5 makar sig tillbaka till sin plats (1)
i) Isobel återställer sig på sin plats. (1)
Summa kostnad: 1 + 1 + 2 + 3 + 0 + 3 + 2 + 1 + 1 = 14

Lösningsalternativ B
Det finns en variant till A där Isobel i stället makar sig in i soffan enligt följande schema:

a) Isobel flyttar sig en liten bit ut från bordet (1)
b) 5 makar sig ut från bordet (1)
c) 3 makar sig ut från bordet (2)
d') Isobel makar sig in till plats 2 (2+1.5=3, se nedan)
e) 1 uttrycker sin vänskap med Isobel (0)
f') Isobel makar sig ut från bordet (2*1.5=3, se nedan)
g) 3 makar sig in till sin plats (2)
h) 5 makar sig in till sin plats (1)
i) Isobel återställer sig på sin plats. (1)
Summa kostnad: Summa kostnad: 1 + 1 + 2 + 3 + 0 + 3 + 2 + 1 + 1 = 14

Isobel behöver här endast förflytta sig två (2) platser vilket ger en kostnad på 2, men eftersom Isobel är fullt påklädd i vacker förvinterskrud medför förflyttning i soffa en något större kostnad per förflyttning, dvs 2 * 1.5 (kostnad 3).

Det är alltså samma kostnad för alternativ A och B (14).


Alternativ C: en mer kostnadseffektiv lösning
Efter snabbt övervägande föreslogs en "proxylösning":


Isobel kramar 5 (0.5)
5 kramar 3 (0.5)
3 kramar 1 (0.5)
1 kramar 3 (0.5)
3 kramar 5 (0.5)
5 kramar Isobel (0.5)
Totalkostnad: 6 * 0.5 = 3.

Eftersom kramar i en soffa förnärvarande har en kostnad på cirka 0.5 skulle detta ge en totalkostand på 6*0.5 = 3 var det naturligtvis bättre än de ovanstående föreslagna alternativa lösningarna.

Alternativ D: mer effektiv lösning och den implementerade
Den lösning som faktiskt implementerades var med (kind)pussar. Som tidigare anges kostnaden inom parentes.

a) 1 pussar 3 (0.1)
b) 3 pussar 5 (0.1)
c) 5 pussar Isobel (0.1)
d) Isobel pussar 5 (0.1)
e) 5 pussar 3 (0.1)
f) 3 pussar 1 (0.1)
Totalkostnad: 0.6

Detta verkar således vara det optimala tidsödande sättet om man använder hälsningsceremonierna kram eller kindpuss.

Kommentarer
I föreslagningsalternativen A och B antogs en kostnad 0 för kram mellan 1 och Isobel men i C antogs den vara 0.5. Hur går detta ihop? Jo, helt enkelt genom att här anta att vinsten för hälsningsceremonin också är 0.5. Detta kan med rätta kritiseras, och man kan här fundera på om det överhuvudtag går att jämföra kostnaden de två principiella olika hälsningsmodellerna:
* direkt hälsningsceremoni, dvs där Lisa och Isobel verkligen hälsar på varandra
* den indirekta ceremonin (proxyvarianten) där hälsningen skrev via andra på platsen närvarande personer.

Om vinsten i den direkta hälsningsmodellen är tillräckligt stor kan alternativ A eller B vara att föredra framför C och D. Vidare forskning - förhoppningsvis kompletterade med empiriska studier - inom området kan förhoppningsvis klargöra detta.

Vidare utökning av modellerna bör även studera de vinster som uppstår hos proxy-personerna. I ovanstående modell har vi helt ignorerat vinsterna för 3 och 5 som får förmånen att interagera med 1, med Isobel samt med varandra. Troligen är sådana vinster inte försummbara.


Två noter
a) Om Isobel eller för den delen 1, 2, 3, 4 respektive 6 skulle känna sig kränkta av ovanstående beskrivning bes det om ursäkt.
b) Det inses snabbt att ovanstående beskrivning - i sin nuvarande form - inte skulle bli publicerad i Hänt-i-Veckan eller liknande förmedlingsmedier, oavsett om det funnes kompletterande tillfällestagna bilder på de alternativa lösningarna. Möjligen skulle bilderna själva kunna publiceras med en något mer snärtig bildtext, t.ex. Algoritmchock kring logistiskt hälsningsceremoniproblem eller - mer troligen - Pusschock med Isobel!.

Posted by hakank at 09:59 EM Posted to Blogging | Matematik | Pyssel | Comments (9)

november 04, 2005

Sesemans matematiska klosterproblem samt lite Constraint Logic Programming

Bengt O. Karlsson ställde igår en matematisk gåta: Ett aritmetiskt problem av Hans Jacob Seseman. Se även den omslutande anteckningen Sesemania (som avslutas med en personlig anmaning). [Uppdatering: Titeln på den nyss angivna anteckningen är felaktig och ska vara Sesemana, men felskrivningen upplevdes av Bengt som en nära-Freud-upplevelse. Och hur kan man underlåta att ge Bengt en sådan njutning? Därför står felstavningen kvar i sin ursprungliga - men alltså felaktiga - prakt. Se något mer i kommentarerna till Bengts Sesemana -artikel. I sanningens namn korrigerades först felet, men sedan korrigerades rättet och denna uppdatering skrev som ett förtydligande.]

Det var ett kul litet problem, och inte speciellt svårt att lösa. En av utmaningarna var att korrekt tolka gammelsvenskan för att förstå vad problemet egentligen bestod av. Försök gärna lösa problemet själv innan ni läser vidare eller läser kommentarerna till problemet.

Uppdatering 2
På begäran har programmet Seseman's Convent Problem (se nedan) nu även möjlighet att visa unika lösningar, eller - mer korrekt - samla lösningar som är lika vad gäller rotation, spegling etc. Denna unicifiering har gjorts i CGI-programmet, ursprungligen som ett analysstöd för att eventuellt senare göra sådant i CLP-programmet.


Problemet
Problemet består av 4 liknande delproblem där det gäller att givet ett visst antal personer i ett kloster (nunnor samt eventuellt "tillkomne Karlar") ska man placera ut dessa personer i rum så att vissa villkor uppfylls.

A, B, C, D, E, F, G, H betecknar klostrets olika rum. Rummet "_" används inte, forutom att presentera en fin kvadrat.

A B C
D _ E
F G H

Ett krav är att vissa rader/kolumner ska ha summan 9:

A + B + C = 9
A + D + F = 9
C + E + H = 9
F + G + H = 9

Ett annat krav är att totalantalet personer ska vara en av de fyra summorna (24, 28,20, 32), som man själv fick lista ut med lite enkelt aritmetik. Villkoret är alltså:


A + B+ C + D + E + F + G + H = Totalsumma

Notera att det inte står någonting om huruvida rum kan vara tomma eller ej (se nedan om detta).

I kommentarerna till problemet visades ett antal olika lösningar, och det visar sig att problemet inte är entydigt eftersom några delproblem har flera lösningar, varav några presenteras av Fredriik och Hakke (också en Håkan K) samt undertecknad (Håkan K).


Constraint Logic Programming
Men det finns fler lösningar än så.

Problemet löstes ursprungligen med penna och baksidan av ett papper, men efteråt skapades ett litet CLP-program (Constraint Logic Programming) för att generera de olika lösningarna, närmare bestämt i det Prolog-baserade programspråket ECLiPSe (Gratis att ladda ner, men man måste anhålla om en licens.)

ECLiPSe-programmet finns här. Den centrala funktionen i programmet innehåller i stort sett endast de matemaitksa uttrycken ovan.

seseman(Rowsum, Total, FirstNum, LD) :-
LD = [A,B,C,D,E,F,G,H], % deklarera variablerna

% FirstNum = 0: empty rooms allowed
% FirstNum = 1: empty rooms not allowed
LD :: [FirstNum..9],

% Radsumma/Kolumnsumma
A+B+C #= Rowsum,
A+D+F #= Rowsum,
C+E+H #= Rowsum,
F+G+H #= Rowsum,

% summan av alla tal = Total
A+B+C+D+E+F+G+H #= Total,

labeling(LD).

Den magiska genereringen av giltiga lösningar enligt restriktionerna (constraints) hanteras av labeling.


För att köra programmet från kommandoraden anger man följande:

eclipse -b seseman.ecl 9 24 1 -e 'go.'

där 9 är radsumman, 24 totalsumman. Talet 1 är ett hack för att ange att inget rum får vara tomt (0 om rum får vara tomma). -e 'go' är anropet till funktionen go och -b anger filnamnet.


Lösningar och ett webb-program
Det skrevs även ett webb-program som kommunicerar med ECLiPSe-programmet: Seseman's Convent Problem (monastary är munkkloster, convent är nunnekloster). Detta program gör det också möjligt att ändra på parametrarna skulle man så önska leka lite.

T.ex. finns det 7 lösningar för totalsumma 20 om man inte tillåter tomma rum och hela 73 lösningar om tomma rum tillåts.

Notera att programmet inte tar hänsyn att två lösningar kan vara samma fast de är roterade, spegelvända etc. Uppdatering Jodå, det gör det nu.

För de fyra olika totalsummorna som angav i problemet förevisas här antalet lösningar och om rum får vara tomma eller ej:
24 personer, tomma rum tillåts ej: 85 lösningar
24 personer, tomma rum tillåts: 231 lösningar

Som problemet är formulerat finns det dock bara en korrekt lösning för första delproblemet (24 nunnor): samtliga rum innehåller vardera 3 nunnor.

28 personer, tomma rum tillåts ej: 35 lösningar
28 personer, tomma rum tillåts: 165 lösningar
20 personer, tomma rum tillåts ej: 7 lösningar
20 personer, tomma rum tillåts: 73 lösningar
32 personer, tomma rum tillåts ej: 1 lösning
32 personer, tomma rum tillåts: 35 lösningar


Programmet har dock kvar begränsningen att maximalt antal personer som får finnas i ett rum är 9. Vi kan väl säga att det beror på att jag vill vara snäll mot webbservern. Om man vill leka med större värden kan man ändra 9 till något annat (t.ex. Total) på denna rad:

LD :: [FirstNum..9],


Kommentarer
Jag har inte hittat någon ren matematisk lösning på problemet, men en sådan kanske kommer (av någon). Ovanstående program gör det i alla fall möjligt att empiriskt studera problemet. Uppdatering: Det finns en bok Sesemans problem som kanske innehålla slika lösningar.


Man kan möjligen misstänka att Fredrik nu kommer att skriva ett mycket elegantare Python-program för detta problem.


För den som vill läsa mer om Constraint Logic Programming kan rekommenderas Programming with Constraints av Kim Marriott och Peter Stuckey. Boken innehåller många exempel som finns att ladda ner.

Posted by hakank at 11:48 EM Posted to Constraint Programming | Matematik | Program | Comments (12)

oktober 28, 2005

Lagoma tal och dess släktingar

I en maildiskussion skrev Mats Andersson följande (något redigerat) apropå ett hotells (*) belägenhet:

sqrt(2) är nog det lagomaste talet som finns. Näst efter Pi. Och E. Och Phi.

Detta gjorde mig nyfiken på definitionen av lagoma tal. google är som vanligt inte till någon hjälp i de allra viktigaste frågorna. Därför är egendefinitioner den enda lösningen. Ett förslag till definiton är alltså följande.


Lagoma tal
Ett lagom tal (ett lagomt tal) är ett tal som är tillräckligt litet för att kunna representera en kort gångsträcka om den representerar kilometer. Exempel på lagoma tal: 1, sqrt(2), E, Phi.

Avståndet får dock inte vara för litet eftersom då får man ingen motion. Se vidare Motionella tal. Kan t.ex. användas för att representera avstånd mellan ett hotell och Slottet (i Stockholm eller annorstädes).

Det finns ännu ingen bevisat både objektiv och effektiv metod att säkerställa ett tals lagomhet. Existensen av de hitills funna lagoma talen har bevisats genom experimentella metoder.


Not: även väldigt små tal kan vara lagoma tal, men då får de inte representera en engångssträcka utan måste vara periodiskt utsträckt över både tid och rum. T.ex. sin(x) kan motsvara ett sådant tal, men man bör dock vara försiktig att använda denna funktion i blåsigt väder utan mössa eller mössliknande öronbeskydd.


Motionella tal
Tal som räknat i kilometer rask gångtakt ger bra motion. Se även Lagoma tal som är något mindre. Se även Nationella tal.


Nationella tal
Tal som endera är ett Lagoma tal eller Motionella tal (vilka se) och avser avstånd inom det egna landet.

Tal som avser avstånd i annat land - eller annorstädes där risken att gå vilse anses vara större - kallas för Irr-nationella tal.


Simmetriska tal
Yngre kusin till Lagoma tal. Tal som avser avstånd i badhus och liknande vattenomslutande inrättningar.


(*) Liten tävling: Den förste som kan korrekt gissa vilket hotell det var som inspirerade till ovanstående bjuds på en öl eller motsvarande vid bästa tillfälle. Varken Mats Andersson eller jag är i stånd att gissa (eftersom vi faktisk vet svaret) och får därför inte vara med i tävlingen.

Posted by hakank at 07:24 EM Posted to Humor | Matematik | Comments (21)

september 04, 2005

Svaren på Augusti-pyssel

Här kommer så de eftersökta (?) svaren på 2005 års Augusti-pyssel. Pysslen är samtliga saker som jag själv leker med från tid till annan.


Fråga 1) Vad står här egentligen och varför (dvs enligt vilken metod): 1045668080


Svar: Det står "hakank" i bas 36. Detta kan lämpligast kontrolleras via programmet base_conv, se vad som står för bas 36. Programmet beskrevs mer i base_conv: Konvertering av ord till tal till ord just som en ledtråd till denna gåta.


Fråga 2) Vad står här egentligen och varför: 15604225

Svar: Det står "messages". Enligt följande mekanism

1. En faktorisering av talet ger följande primtal: 5, 7,13, dvs 15604225 = 5^2 * 7 * 13 * 19^3.

2. Om man tar positionerna i alfabetet "a".."z" och låter "a" har position 1, "b" position 2 etc, för dessa faktorer får man bokstäverna: "e", "g", "m", "s". Faktorn 5^2 motsvarar två stycken "e", 7^1 motsvarar ett "g" etc. Hela denna konvertering skapar bokstäverna: "e","e","g","m","s","s","s" enligt följande:

alpha = "abcdefghijklmnopqrstuvxyz"
alfa[5] = e # 5^2 : 2 stycken e
alfa[7] = g # 7^1: 1 styck "g"
alfa[13] = m # 13^1: 1 styck "m"
alfa[19] = s # 19^3: 3 styck "s"

Eftersom talet 1 (som motsvarar "a") alltid är en giltig faktor så kan denna bokstav också ingå. Den slutliga bokstavsmassan blir alltså

0 eller flera "a" (här behövs exakt ett "a")
e
e
g
m
s
s
s

dvs e e g m s s s samt eventuellt ett gäng a.


Efter lite anagrammerande kryper det korrekta svaret "messages" fram..

OK, a-konstruktionen gjorde det kanske onödigt svårt, och var det som antyddes i den uppdaterade kommentaren på Augusti-pyssel-sidan. Sorry 'bout that.

Fråga 3) Vad ska stå i stället för "?" i nedanstående?

Så kommer vi till sekvenserna där bara ett tal var givet. I kommentarerna gavs sedan en ledtråd med det omedelbart föreliggande talet.

a) ...., 1596, ?

Svar: 2583. Detta är summan av de 15 första Fibonacci-talen och svaret är det 16:e talet i denna serie, dvs 2583.


# Fibonacci talen
> fibonacci(i)$i=1..15;
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610


# summan av de 14 första
> sum(fibonacci(i),i=1..14);
986

# 15 första
> sum(fibonacci(i),i=1..15);
1596

# och så de 16 första
> sum(fibonacci(i),i=1..16);
2583

# hela serien
> seq(sum(fibonacci(i),i=1..a), a=1..16);
1, 2, 4, 7, 12, 20, 33, 54, 88, 143, 232, 376, 609, 986, 1596, 2583

Sekvensen som fås av summan av de första a Fibonacci-talen är för övrigt 1 snäpp ifrån Fibonacciserien:

> seq(sum(fibonacci(i),i=1..a)+1, a=1..16);
2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584

Eller snarare: Det är en Fibonacci-liknande rekursiv serie där men i stället för att utgå från (1,1) som generatorer utgår man från (1,2).


b) ...., 78, ?

Svar: 91. Serien är addition av de a (12) första naturliga talen och nästa tal är det 13 talet i denna serie.


> 1+2+3+4+5+6+7+8+9+10+11;
66

> 1+2+3+4+5+6+7+8+9+10+11+12;
78

> 1+2+3+4+5+6+7+8+9+10+11+12+13;
91

# hela serien
> seq(sum(i,i=1..a),a=1..13);
1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91


c) ...., 129, ?

Svar: 160. Detta är summering av de första primtalen och svaret är det 11 talet i denna serie: 160 som fås när man adderar 31 till 129 = 160.


> ithprime(i)$i=1..10;
2, 3, 5, 7, 11, 13, 17, 19, 23, 29


> 2+3+5+7+11+13+17+19+23;
100

> 2+3+5+7+11+13+17+19+23+29;
129

> 2+3+5+7+11+13+17+19+23+29+31;
160

# hela serien
> seq(sum(ithprime(i),i=1..a),a=1..11);
2, 5, 10, 17, 28, 41, 58, 77, 100, 129, 160


Fråga 4) Vad är det gemensamma för nedanstående ord?
* besökes
* eksem
* gömmes
* webb


Svar: Samtliga dessa ord innehåller endast bokstäver med primtalspositioner (cf diskussionen kring fråga 2). Primtalsbokstäverna är alltså där positionen står först. (Not: positionen 1 för "a" har jag redan bett om ursäkt för.)

1:a
2:b
3:c
5:e
7:g
11:k
13:m
17:q
19:s
23: w
29:ö

Orden med respektive faktorer:
* besökes: 5757950 = 2 * 5^2 * 11 * 19^2 * 29
* eksem: 67925 = 5^2 * 11 * 13 * 19
* gömmes: 3259165 = 5 * 7 * 13^2 * 19 * 29
* webb: 460 = 2 * 5 * 7^2

Notera att orden inte innehåller samma antal faktorer (antal bokstäver) som det givna talet, utan är ord som endast innehåller dessa bokstäver oavsett hur många förekomster av bokstaven som ingår. Denna fråga var mestadels med som en ledtråd till fråga 2.

Posted by hakank at 12:24 EM Posted to Matematik

augusti 29, 2005

Kortsamlarproblemet (coupon collector problem) i mindre och isolerade nätverk med fullständigt utbyte av kort

Introduktion

När jag var liten samlade jag en hel del på samlarkort, t.ex. flaggor, ishockey-/fotbollsspelare etc. Det var alltså sådana kort där man köpte osett, ett eller flera kort i en påse (med eventuellt medföljande tuggummi eller annat godis) och sedan antingen köpte man nya eller bytte man till sig de kort man inte hade. Den stora poängen var naturligtvis att få hela serien komplett. (Det fanns säkert en fin social poäng i att träffas och byta sådana kort, men sådana finesser uppfattade man nog inte i denna ålder, typ kring 10+ år.)

Speciellt för flaggorna kommer jag ihåg att det fanns vissa kort som var väldigt svåra att få tag på (var det Mexiko med nummer 104, eller kanske var det Kenya?). Om jag nu kommer ihåg detta korrekt var det några få lyckostar som fått detta kort och vi andra dräglade djupt över dessa rara kort.


Kortsamlarproblemet (coupon collector problem)
Det finns ett klassiskt problem inom statistiken/sannolikhetsläran som handlar om detta: kortsamlarproblemet (coupon collector problem, dvs kupongsamlarproblemet) där man studerar hur många kort man behöver köpa i genomsnitt (eller för en viss säkerhetsgrad) på att få samtliga kort i en sådan samlarserie. Det visar sig att det är ointuitivt många: För att få tag i samtliga kort i en serie av 100 kort behöver man i medeltal köpa 519 kort. (Enkel formel för detta : 100*sum(1/(1:100)) ~ 519, där 100 i formeln är just antal unika kort i samlarserien.)

Men detta antal fluktuerar naturligtvis: för att vara säker till 95% att få tag i samtliga kort krävs 791 inköpta kort. Se även min Simuleringssida för lite mer om detta; sök på "samlarkortproblemet ".

Man kan notera att ovanstående beräkningar endast gäller för en person som ensam inhandlar kort. Om man tillåter byte av kort är det en annan sak, och det är precis det som det följande kommer att handla om.


Samlarkortproblemet i ett isolerat nätverk med fullständigt utbyte
För ett tag sedan hade jag en diskussion med en kompis om detta. Denne - som vi kan kalla för E - hävdade att företagen troligen inte tillverkar lika många av varje kort, just för att få oss att köpa fler kort för att få tag i samtliga.

Denna konspirationsteori är möjligen korrekt, men jag började undra om denna effekt kunde uppstå även om företaget tillverkade lika många exemplar av alla kort, och att det vi råkat ut för var en "klustereffekt", dvs att de kort som vi i vårt lilla nätverk var en slumpmässigt urval med de traditionella egenskaperna hos sådana urval.

E antog att företagen som skapar korten alltså tillverkar vissa kort i färre upplagor, säg att de färsta (sic!) är en tiondel av de som tillverkas mest. Min utgångspunkt var att denna effekt skulle kunna vara subjektiv enligt "regeln" att om man slumpmässigt drar ett antal olikfärgade kulor från en påse med lika fördelning så är det mycket stor sannolikhet att något antal är färre än de övriga och att det finns en färg som dras fler gånger.

Detta är något man kan testa med en simulering. Vilket har gjorts.


Sammanfattning
Som vi kommer att se uppstår faktiskt denna typ av effekt (E-effekt) om det totalt köps in ett mindre antal samlarkort. För 700 inköpta kort blir förhållandet mellan minst antal kort och flest antal kort rätt exakt 1/10.

Här nedan kommer även andra saker att visas, t.ex. denna effekt hos Lotto-dragna nummer, där samma förhållande är 1/2, vilket även uppstår i en simulering. Kanske inte så remarkabelt men intressant.


Lokalt nätverk med fullständigt utbyte av samlarkort
Först en sak om nätverket. Den modell som vi här arbetar med innebär att det finns en mindre grupp, säg ett 10-tal personer, som har fritt utbyte av samlarkort inom gruppen men inte har något som helst kort-utbyte med några externa personer eller andra nätverk. Denna fullständiga isolering av inköpen gör modellen enkel att simulera.

(Man skulle även kunna studera komplexa nätverks-effekter kring detta, dvs att någon i Husieskolans krets känner någon i Stockholm och byter till sig de i Husie-kretsens ovanliga kort. Ju fler sådana svaga länkar mellan olika (inte helt isolerade) nätverk det finns, desto större blir naturligtvis den totala kretsen vilket leder till att denna lokala nätverkseffekt vi talar om här blir mindre.)


Modell och simulering
Tänk nu följande som översättning av samlarkortproblemet i ett lokalt nätverk till slumpmässig dragning av heltal i ett intervall.

En grundläggande förutsättning är att det faktiskt skapas exakt lika många kort, och att man globalt har lika stor chans att köpa alla kort, men vi studerar endast en mindre krets (nätverk) av personer som får tillgång till ett urval av dessa, t.ex. där tobakaffärens och den där kioskens urval.

Låt oss för enkelhetens skull anta att samlarkortserien har 100 olika kort. Dessa 100 olika korten motsvaras i simuleringen då av de första 100 positiva heltalen (1..100 alltså). Ett inköp av ett kort motsvarar att man slumpmässigt drar ett tal inom detta intervall, där alla tal har lika stor chans att dras. Detta görs s.a.s. med återläggning, så att ett tal har möjlighet att dragas igen.

Man drar slumpmässigt n stycken sådana tal, vilket alltså motsvarar inköp av n stycken samlarkort.

Efter det beslutade antalet "kort" (tal) är dragna, kontrolleras fördelningen bland dessa kort. Här jämför man antalet kort som kommit upp med minst antal och de som kommit med flest antal. Om ss är listan över de dragna talens fördelning är det sökta värdet alltså: min(ss)/max(ss), det som nedan kallas för min/max-förhållandet.

Vi behöver inte förutsätta något om hur stor gruppen är eller hur många kort en specifik deltagare införskaffar. Vi kommer senare se hur många fullständiga serier ett visst antal inköpta kort tenderar att generera, och man kan alltså anpassa antalet kort som (i medeltal) behöver köpas in för att få fullständiga serier.


Frågeställningen och hypotesen
Låt oss alltså se hur fördelningen mellan minimi-antalet kort och maximi-antalet kort utvecklas med det totala antal kort som inköpes.

Frågeställningen: Vad är förhållandet mellan min/max om det totalt köps in num.bought stycken kort av num.cards möjliga?

Hypotes: Om man slumpmässigt kommer fram till sådana min/max-förhållande på säg 1/10 eller något liknande har vi inget statistiskt stöd för E:s konspirationsteori.

Här följer R-koden som använts för simuleringen, som helt enkelt drar num.bought stycken tal ur intervallet 1..num.cards och returnerar fördelningen av de dragna talen (dvs hur många 1:or som dragits, hur många 2:or etc). Man kan här också notera hur enkelt denna simulering är. Det beror på att vi gjort det enkelt för oss och förutsatt att det fullständigt och fritt utbyte i detta isolerade nätverk.


collector.group.sim <- function(num.cards=100, num.bought=10000) {
ss <- rep(0,num.cards);
for (i in 1:num.bought) {
s <- sample(1:num.cards,1);
ss[s] <- ss[s] + 1;
}
ss
}


Exempel:
Om vi nu antar att det är 100 olika kort och 10 personer som samlar, samt att dessa vardera köper respektive 200 kort, inalles 10*200 = 2000 kort. En sådan simulering ser ut så här (sorterad lista eftersom vi inte behöver bry oss om de specifika talen/korten som dragits):


> ss<-collector.group.sim(100, 10*200);sort(ss);min(ss);max(ss);min(ss)/max(ss)
[1] 10 11 12 12 12 13 14 14 14 15 15 15 16 16 16 16 16 16 17 17 17 17 17 17 17
[26] 17 18 18 18 18 18 18 18 18 19 19 19 19 19 19 19 19 19 19 19 19 20 20 20 20
[51] 20 20 20 20 20 20 20 20 20 20 20 20 21 21 21 21 21 21 21 21 21 22 22 22 22
[76] 22 22 23 23 23 23 24 24 25 25 25 25 25 25 26 26 26 27 27 27 27 28 28 33 33
[1] 10
[1] 33
[1] 0.3030303
> 10*200
[1] 2000

Här kan vi alltså se att det minsta antalet dragna tal/kort är 10, dvs min(ss), och max är 33. Förhållandet mellan dessa min(ss)/max(ss) är 10/33 ~ 0.3. Redan enna enkla simulering (detta nätverk) ger en känsla av att vissa kort är ovanligare än varandra, och förhållandet mellan de ovanligaste och de vanligaste är 10 på 33.

Personligen tycker jag detta är emot intuitionen: efter en slumpmässig dragning har vi ett min/max-förhållande på så stort som 0.3.


Om vi istället säger att man tillsammans endast köper 519 kort (dvs så många som det i genomsnitt krävs för att en person ska få en komplett serie) får vi några intressanta resultat. Notera att även här är det endast en enda körning, för att få en känsla för datan.


> ss<-collector.group.sim(100, 519);sort(ss);min(ss);max(ss);min(ss)/max(ss)
[1] 1 1 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4
[26] 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 5 5 5
[51] 5 5 5 5 5 5 5 5 5 5 5 5 5 6 6 6 6 6 6 6 6 6 6 6 6
[76] 7 7 7 7 7 7 7 7 7 7 7 8 8 8 8 8 8 8 9 9 10 10 11 12 13
[1] 1
[1] 13
[1] 0.07692308

Här kan till exempel följande noteras:

* min/max-förhållandet är värre än E:s föreslags 1/10, nämligen 1/13 (0.077)

* det minsta talet är 1 vilket innebär att det finns kort för en fullständig serie. (Fullständiga serier kommer att studeras mer här nedan.)


Vi gör nu en mer statistisk korrekt simulering med 100 sådana här simuleringar och tar medelvärdet för min/max-förhållandet:

> mean(replicate(1000,{ss<-collector.group.sim(100, 519);min(ss)/max(ss)}))
[1] 0.05141527

min/max-talet 0.05 (~ 1/20) stödjer ovanstående känsla att det är värre min/max-förhålllande än E:s 1/10.

Men det är kanske inte så realistiskt att en grupp tillsammans köper endast 519 kort? Låt oss nu titta på hur min/max-förhållandet påverkas av antalet inköpta kort.


Tabell över (medelvärde) av min/max-förhållandet för olika antal kortinköp
Om vi nu studerar medelvärdet av min/max för olika antal kortinköp får man följande tabell.

Från 100 inköp till 3000

> sapply(1:30, function(n) rbind(n*100, mean(replicate(100,{ss<-collector.group.sim(100, n*100);min(ss)/max(ss)})) ))
[,1] [,2] [,3] [,4] [,5] [,6] [,7]
[1,] 100 200 300 400.00000000 500.00000000 600.00000000 700.0000000
[2,] 0 0 0 0.01154701 0.04447036 0.07848971 0.1029102

[,8] [,9] [,10] [,11] [,12]
[1,] 800.0000000 900.0000000 1000.0000000 1100.0000000 1200.0000000
[2,] 0.1298539 0.1475774 0.1695608 0.1864951 0.1996583

[,13] [,14] [,15] [,16] [,17]
[1,] 1300.0000000 1400.0000000 1500.0000000 1600.0000000 1700.0000000
[2,] 0.2132364 0.2434604 0.2501553 0.2677531 0.2798811

[,18] [,19] [,20] [,21] [,22]
[1,] 1800.0000000 1900.0000000 2000.0000000 2100.0000000 2200.0000000
[2,] 0.2819174 0.2909844 0.3101849 0.3119899 0.3260513

[,23] [,24] [,25] [,26] [,27]
[1,] 2300.0000000 2400.0000000 2500.0000000 2600.0000000 2700.0000000
[2,] 0.3373065 0.3520848 0.3504074 0.3622678 0.3721507

[,28] [,29] [,30]
[1,] 2800.0000000 2900.0000000 3000.00000
[2,] 0.3841707 0.3844286 0.38901

Här kan man se att gränsen för 1/10 i förhållande mellan min och max är cirka 700 inköp. Detta motsvarar en liten grupp på 7 personer som köper vardera 100 kort, eller 4 personer som köper 175 kort osv. Jag tycker att det låter rätt lite, men å andra sidan var E:s 1/10 taget ur luften.

Om vi tar lite större steg: mellan 1000 till 30000 inköp:

> sapply(1:30, function(n) rbind(n*1000, mean(replicate(100,{ss<-collector.group.sim(100, n*1000);min(ss)/max(ss)})) ))
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 1000.0000000 2000.0000000 3000.0000000 4000.0000000 5000.0000000 6000.0000000
[2,] 0.1684101 0.3033053 0.3869192 0.4466518 0.4883167 0.5158891
[,7] [,8] [,9] [,10] [,11] [,12]
[1,] 7000.0000000 8000.0000000 9000.0000000 10000.0000000 11000.0000000 12000.0000000
[2,] 0.5387887 0.5611546 0.5857873 0.6023973 0.6199602 0.6338816
[,13] [,14] [,15] [,16] [,17]
[1,] 13000.0000000 14000.0000000 15000.0000000 16000.000000 17000.0000000
[2,] 0.6371665 0.6508695 0.6613642 0.665185 0.6797338
[,18] [,19] [,20] [,21] [,22]
[1,] 18000.0000000 19000.0000000 20000.0000000 21000.0000000 22000.0000000
[2,] 0.6845181 0.6965812 0.6978221 0.7095483 0.7138271
[,23] [,24] [,25] [,26] [,27]
[1,] 23000.0000000 24000.0000000 25000.0000000 26000.000000 27000.0000000
[2,] 0.7187094 0.7274481 0.7267149 0.733775 0.7309658
[,28] [,29] [,30]
[1,] 28000.0000000 29000.0000000 30000.0000000
[2,] 0.7380007 0.7450008 0.7422353


Exempel: I vårt lilla samlarkortnätverk var vi väl 10 stycken och köpte kanske 150
kort per person, dvs total 10*150 = 1500 inhandlade kort. I tabellen ser man att
förhållandet mellan antalet färst kort och antalet flest kort är 0.25 (1/4), vilket
troligen skulle kunna uppfattas som den E-effekt vi talade om i början.

Ännu större inköp som tar riktigt lång tid att simulera: för 100000 inköpta kort blir medelvärdet av min/max cirka 0.85 (0.8506242). För en miljon inköp är det 0.9512054.

Vi ser alltså att min/max-förhållandet tenderar att utjämnas då antalet inköp ökar, vilket är vad man kan förvänta sig enligt de stora talens lag.


Fullständiga serier i nätverket
Ser man på minimivärderna för dessa får man antalet (genomsnittligt uppkomna) fullständiga serier i nätverket. Detta förutsätter alltså att alla i nätverket byter rakt av och inte är snikna eller har orealistiska byt-krav.


> sapply(1:30, function(n) rbind(n*1000, mean(replicate(100,{ss<-collector.group.sim(100, n*1000);min(ss)})) ))
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9]
[1,] 1000.00 2000.00 3000.00 4000.00 5000.0 6000.0 7000.00 8000.00 9000.00
[2,] 3.08 9.71 17.08 24.98 33.2 41.2 49.87 59.03 66.67

[,10] [,11] [,12] [,13] [,14] [,15] [,16] [,17]
[1,] 10000.00 11000.00 12000 13000.00 14000.00 15000.00 16000.00 17000.00
[2,] 76.01 84.79 94 102.37 111.52 120.41 128.45 138.62

[,18] [,19] [,20] [,21] [,22] [,23] [,24] [,25]
[1,] 18000.00 19000.00 20000.00 21000.00 22000.0 23000.00 24000.00 25000.00
[2,] 147.44 156.05 165.46 173.09 184.5 192.92 202.72 212.33

[,26] [,27] [,28] [,29] [,30]
[1,] 26000.00 27000.00 28000.00 29000.00 30000.00
[2,] 220.74 229.74 238.11 248.47 257.23

Dvs om 3 (3.08 i tabellen ovan) personer tillsammans köper 1000 kort får de (i medelvärde) alla får en fullständig serie. På samma sätt om 9 (9.71) personer köper 2000 kort, 17 (17.08) köper 3000 kort så bör de i genomsnitt få fullständiga serier. Osv.

Fokuserar här in på 100 .. 3000 kortinköp:

> sapply(1:30, function(n) rbind(n*100, mean(replicate(100,{ss<-collector.group.sim(100, n*100);min(ss)})) ))
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11]
[1,] 100 200 300 400.00 500.00 600.00 700.00 800.00 900.0 1000.00 1100.00
[2,] 0 0 0 0.13 0.57 1.05 1.48 1.97 2.5 3.17 3.69

[,12] [,13] [,14] [,15] [,16] [,17] [,18] [,19] [,20] [,21]
[1,] 1200.00 1300.00 1400.00 1500.0 1600.0 1700.00 1800.0 1900 2000.00 2100.00
[2,] 4.44 4.99 5.63 6.1 7.3 7.97 8.3 9 9.91 10.41

[,22] [,23] [,24] [,25] [,26] [,27] [,28] [,29] [,30]
[1,] 2200.00 2300.00 2400.00 2500.00 2600.00 2700.00 2800.00 2900.00 3000.00
[2,] 11.17 11.95 12.79 13.53 13.93 15.09 15.85 16.16 17.21

Här ser vi också en-person-problemet: för 600 inköp är det drygt en person som får en full serie, det "exakta" väntevärdet är alltså 519.


Några noteringar
Lite av det vi set ovan:

* Om det är få inköps (säg < 700) får man alltså den 1/10-effekt som både E och jag upplevde i våra respektive barndomar. Det behövs alltså inte någon konspirationsteori för att förklara detta. (Naturligtvis kan detta kombineras med att kort-företaget faktiskt gjorde denna 1/10-tillverkning, men dessa experiment stödjer alltså inte detta.)

* Nätverkets storlek, dvs antalet personer som ingår i det, är inte viktig i denna modell, utan det som är avgörande är hur många kort man tillsammans köper. Det kan vara en person som köper 10000 och de andra 100 stycken, och tillsammans har de alltså 10000+ 10*(N-1) kort vilka sedan kan bytas hur som helst.

Samt en sista notering:

För 519 inköp i ett utbytesnätverk blir det igenomsnitt så här många fullständiga serier:

> table(replicate(1000,{ss<-collector.group.sim(100, 519);min(ss)}))/1000

0 1 2
0.409 0.563 0.028

Vilket är intressant eftersom det i 2.8% av fallen faktiskt skapas 2 stycken fullständiga serier (trist nog befann man sig aldrig i dessa nätverk :). 519 inköpta kort är, som sagt, det magiska medeltalet för att en person skulle få en fullständig serie.


Jämförelse: min/max-analys av svenska Lottodragningar
Här görs en motsvarande min/max-analys av svenska Lottodragningar. I går inhämtades fördelningen av senaste halvårets lottodragningar. (Värdena hämtas från Svenska Spel: klicka på den gröna Lotto-bilden/knappen, och i den uppkomna popuppen klicka på den gröna "Statistik"-knappen.)

Fördelningen av de 35 Lotto-talen är att det minst dragna talet har endast dragits 22 gånger (faktiskt två tal), och det mest dragna talet har dragits 44 gånger. En sorterad fördelning av talen ser ut så här:

> lotto2<-read.table("svensk_lotto2.dat",head=T, sep=",")
> sort(lotto2$dragna)
[1] 22 22 23 24 27 28 28 29 30 30 30 31 31 31 31 32 32 32 32 33 34 35 35 35 35
[26] 36 37 37 38 38 39 40 40 43 44

> sum(lotto2$dragna)
[1] 1144

> min(lotto2$dragna);max(lotto2$dragna)
[1] 22
[1] 44

> min(lotto2$dragna)/max(lotto2$dragna)
[1] 0.5

Det ger alltså ett min/max-förhållande på 22/44 = 0.5. Är det något lurt här? Låt oss ser hur en simulering beter sig. Det är alltså totalt 1144 dragna tal de senaste halvåret och det finns 35 tal, vilket - för att prata i samlarkortproblemets terminologi - motsvarar 35 "kort" och 1144 "inköpta kort"

En exempelkörning:

> sort(ss<-collector.group.sim(35, 1144))
[1] 22 22 22 24 24 26 27 27 28 29 29 29 31 31 32 32 32 33 33 33 33 34 34 35 36
[26] 37 39 39 39 40 41 42 43 43 43

> min(ss)
[1] 22
> max(ss)
[1] 43
> min(ss)/max(ss)
[1] 0.5116279


Medelvärdet för 100 sådana min/max-simuleringar är cirka 0.47, vilket är tillräckligt nära Lotto:s min/max-värde på 0.5 för att vi ska känna oss trygga att Lotto-dragningar inte är påtagligt konstiga.


> mean(replicate(100, {ss<-collector.group.sim(35, 1144);min(ss)/max(ss)}))
[1] 0.466839


Slutkomihåg
I en samling slumpmässiga dragningar som Lotto eller samlarkort är det alltid någon eller några bollar/kort/tal som slumpmässigt dras fler gånger än de övriga, liksom det är alltid någon eller några som dras färre gånger än de övriga.

Man kan förledas att tro att det är något signifikant (speciellt, konstigt, magiskt) med dessa olika extremvärdena, speciellt om det är ett mindre antal dragningar som studerats. Sådana felslut kallas för "The extreme value fallacy" (se nedan).


Se även
Extremvärdesanalys av webbesök, speciellt länken till Number Watch: The extreme value fallacy.

Födelsedagsparadoxen/födelsedagsproblemet: Se t.ex. Sammanträffanden - anteckningar vid läsning av Diaconis och Mosteller 'Methods for Studying Coincidences' (teknisk, men länkar i slutet till andra sidor) samt .

Födelsedagsproblemet kan kanske ses som ett komplement till samlarkortproblemet: I födeledagsproblemet studerar man hur många personer det minst måste vara för att två (eller fler) ska ha samma födelsedag. I samlarkortproblemet är det frågan om hur många personer det måste vara för att alla dagar på ett år ska ha åtminstone en person som har födelsedag på denna person: Enligt det klassiska samlarkortproblemet (för en person som själv samlar kort) är det 365*sum(1/(1:365)) ~ 2365.

En Java-simulering: Coupon Collector Problem, från den trevliga sajten Probability by Surprise.

Posted by hakank at 07:27 EM Posted to Matematik | Sammanträffanden | Statistik/data-analys | Comments (2)

augusti 27, 2005

base_conv: Konvertering av ord till tal till ord

Som hjälp för Mats Anderssons födelsedagsgratulationshälsningshuvudbry samt ledtråd till en av gåtorna i Augusti-pyssel publiceras nu ett litet program: base_conv: Yet another word to number to word conversion.

Principen är enkel: Man utgår endera från ett "ord" eller från ett decimaltal varpå programmet konverterar till ett decimaltal respektive "ord" för så många baser som möjligt, från bas 2 till bas 68.


Exempel
T.ex. konverteras "ordet" blogg till decimaltalet 4640416 om blogg ses i bas 25. Bas 25 är för övrigt den minsta basen som kan representera detta "ord" eftersom "o" kräver åtminstone denna bas.

På samma sätt converteras "ordet" Håkan Kjellerstrand (utan mellanslag) i bas 68.till decimaltalet 661332330234565441547965347086985. Äsch, ni kan se hela listan här.


Språk, giltiga tecken
Det finns val för två olika språk med lite olika teckenuppsättning:
* engelska: 0..9 a-z A-Z
* svenska: 0..9 a-zåäö A-ZÅÄÖ

VI kan här se att både de små bokstäverna finns representerade och är väldigt olika. T.ex. "ordet" "åtgärdsförslag" (bas 45: 113728508327740105458241) är inte samma som "ÅTGÅRDSFÖRSLAG" som faktiskt inte ens går att representera i bas 45, eftersom "Ö" kräver bas 68, men det motsvarar decimaltalet 43778068670461409051480041 (sett i bas 68).


Ord, förresten
Konverteringen från decimaltal till "ord" skapar sällan ett "ord" utan är nästan alltid och för de högre baserna en blandning av siffror och bokstäver (förutom då man använder ett tal som konverterats från ett "ord", vill säga), och än mer sällan ett korrekt ord i respektive språk.


Mellanslag och andra lustiga tecken
Programmet tillåter alltså bara ovanstående tecken. Om andra tecken finns i ordet kommer ett felmeddelande. Mellanslag tas dock sonika bort.


En undring
Genom denna typ av konvertering kanske dubbeltydligheten i "tal" fått en praktisk mening. Möjligen kommer "riksdagstal" och 2672678331353573021 (bas 50) att användas omvartannat i framtiden?


Eventuell framtida utveckling
Jag har en liten idé om att göra någon form av "ordfaktorisering", med ungefär följande idéräcka:
* ett ord konverteras till decimaltal (för någon bas)
* decimalet faktoriseras
* faktorerna konvereras tillbaka till "ord" (i någon bas)
* om ett sådant "ord" finns i en ordlista ... vore det skoj.

Ta t.ex. "riksdagstal" (bas 50) = 2672678331353573021. Decimaltalets faktorer är:
174696276315679 samt 15299.

Visst skulle det vara lite skoj om "qqaicähbA" (bas 40 = 174696276315679) vore ett ord i svenskan. 15299 motsvarar en del kortare "ord": t.ex. "obo" (bas 25), "mgb" (bas 26), "kqh" (bas 27), "jeb" (bas 28).

Får se om det blir något med detta.


Programspråk
Programspråket som används för denna utilitet är Ruby (speciellt skoj när man vill rota i klasserna Integer och String.)

Posted by hakank at 10:32 FM Posted to Matematik | Program | Språk

augusti 25, 2005

Talklockor: Något om primtal och sammansatta tal


[Not: Ett primtal är ett tal som endast går jämnt ut vid division med sig själv och 1. Alla andra tal är sammansatta. Både 0 och 1 är lite lustiga i sammanhanget: tekniskt sett uppfyller talet 1 villkoret för primtal, men av hävd anses det inte vara ett sådant. Så 2 är det första primtalet, sedan 3, 5, 7, 11 osv. 0 är ännu mer speciellt eftersom man inte får/kan dela med 0.]


Introduktion
Jag började nyss bläddra i boken Dr Riemann's Zeros som handlar om Riemannhypotesen, ett av de få kvarvarande klassiska matematiska problemen). Målgruppen för boken är icke-matematiker, och saker förklaras verkligen från grunden. T.ex. finns det appendix för ett flertal olika begrepp. Klart lovvärt.


Modeller för primtal och sammansatta tal
Ett av bokens sätt (modell) att beskriva primtalen och de sammansatta talen är att primtalen motsvarar atomer (är odelbara) medan de övriga talen - de sammansatta - motsvarar molekyler som byggs upp av primtalen.

Även om det egentligen inte är något fel på denna bild (förutom att atomer inte är odelbara) så är jag inte riktigt nöjd med den, främst eftersom det - enligt min mening - komplicerar bilden av talen, och gör det kanske svårare än vad det behöver vara. (Det är en annan sak att primtal/sammansatta tal även har denna atomära/sammansatta egenskap.)

Någon gång på 80-talet satt jag med en enkel miniräknare och anteckningsblock och funderade på denna typ av tal och hittade då en annan bild som jag tycker är naturligare för hur talen "fungerar". Till skillnad från atom/molekylmodellen såg jag inte primtalen som de primära utan de blev mer som en logisk (kon)sekvens av en annan egenskap (som förklaras nedan).

Jag ska här visa två metoder att se primtalen och de sammansatta talen som gör att det kanske inte blir så konstigt, utan att det faktiskt hänger ihop på ett trevligt sätt. Det som följer är i någon mening självklart för en matematisk insatt, och för inte matematiken framåt. T.ex. kan man med detta inte lösa Riemann-problemet eller faktorisera större primtal. Men eventuellt kan det avhjälpa vissa icke-matematikers rädslor för primtal och andra matematiska djur. (För säkerhets skull bör nämnas att jag inte är matematiker, men det var länge sedan jag förlorade min matematiska oskuld...)


"Talklockor"
Det sätt jag nu ibland ser talen är att de är uppbyggda av "klockor" som snurrar runt, runt med "ett tick per tal" (ett klockslag per tal). Det speciella med dessa klockor är att de alla har olika storlek, olika urtavlor. De första talen, från 0 till 5 har urtavlorna:

0: har urtavlan (0, dvs alltid 0)
1: har urtavlan (1, dvs alltid 1)
2: har urtavlan (0,1),
3: har urtavlan (0,1,2),
4: har urtavlan (0,1,2,3)
5: har urtavlan (0,1,2,3,4)
...

Generellt har talet n urtavlan (0,1,2,3,...n-2, n-1). Precis som för en vanlig klocka så börjar man om igen från 0 när det behövs, så att för 5-klockan gäller 4 + 1 = 0. 5-klockan skapar alltså av följande sekvens: 0,1,2,3,4,0,1,2,3,4,0,.....

(Både 0 och 1 är som ovan sagt lite konstiga varelser och är med för fullständighets skull både här och nedan.)


Modulo-operatorn
Det finns faktiskt något som ibland kallas för "klockmatematik" och som fungerar precis enligt denna princip: i stället för att fortsätta en sekvens i all oändlighet börjar man om från början när man kommer till urtavlans topp igen. Den matematiska operation kallas bl.a. för modulo-operation (förkortad mod här) och dess resultat är resten vid en division av ett tal med ett annat.

Exempel: mod(10,3) = 3 och 1 i rest. mod(10,5) = 0, eftersom 10 delat med 5 går jämnt ut (ingen rest).

Så här ser hela 10-klockan ut för modulo-operationen (för talen mindre än 10).

10 mod 1 = 0
10 mod 2 = 0
10 mod 3 = 1
10 mod 4 = 2
10 mod 5 = 0
10 mod 6 = 4
10 mod 7 = 3
10 mod 8 = 2
10 mod 9 = 1
10 mod 10 = 0

Not: För mod(m, n) och n > m så är resultatet m, t.ex. mod(10,21) är 10.

Ser man mod(10)-sekvensen, 0,0,1,2,0,4,3,2,1, verkar det inte vara så mycket till struktur i talen. (Det finns naturligtvis en struktur, men mer om detta en annan regnig dag. Här är dock en ledtråd: de sista 5 talen är alltid en fallande serie av tal, ... 4,3,2,1,0 . Talen som kommer före beter sig lite mer intrikat.)


Modulo-tabellen
Det blir mer överskådligt om man gör en tabell för modulo-operationen, med mod(radtal, kolumntal). Talet 0 innebär att det inte finns någon rest vid division, står det 1 innebär det att resten var 1 vid divisionen etc.

Exempel: mod(10,3) = 1. Här ser man 1 där 10-raden och 6-kolumnen korsas. Och mod(12, 6) = 0, som sig bör (eftersom 12 / 6 är 2 och ingen rest). De fetade raderna motsvarar primtalen, och som vi kommer till mycket snart.


___1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
0
1: 0 1
2: 0 0 2
3: 0 1 0 3
4: 0 0 1 0 4
5: 0 1 2 1 0 5
6: 0 0 0 2 1 0 6
7: 0 1 1 3 2 1 0 7
8: 0 0 2 0 3 2 1 0 8
9: 0 1 0 1 4 3 2 1 0 9
10: 0 0 1 2 0 4 3 2 1 0 10
11: 0 1 2 3 1 5 4 3 2 1 0 11
12: 0 0 0 0 2 0 5 4 3 2 1 0 12
13: 0 1 1 1 3 1 6 5 4 3 2 1 0 13
14: 0 0 2 2 4 2 0 6 5 4 3 2 1 0 14
15: 0 1 0 3 0 3 1 7 6 5 4 3 2 1 0 15
16: 0 0 1 0 1 4 2 0 7 6 5 4 3 2 1 0 16
17: 0 1 2 1 2 5 3 1 8 7 6 5 4 3 2 1 0 17
18: 0 0 0 2 3 0 4 2 0 8 7 6 5 4 3 2 1 0 18
19: 0 1 1 3 4 1 5 3 1 9 8 7 6 5 4 3 2 1 0 19
20: 0 0 2 0 0 2 6 4 2 0 9 8 7 6 5 4 3 2 1 0 20

Kolumnerna är alltså klocksekvenserna: Kolumnen för 6 ger klocktalen för 6, dvs 0,1,2,3,4,5,0,1,2,3,4,5,0,1,2,..: en evigt snurrande klocka.


Primtalen i en modulo-tabell
Nu kan vi äntligen börja prata om primtal.

Ett tal är ett primtal om talets rad "råkar" vara så beskaffad att alla klockorna (kolumner) är något annat än 0 för kolumnerna som motsvarar mindre tal än radtalet, förutom för 1-kolumnen och talets egen kolumn. Det sistnämnda är helt som det ska eftersom definitionen av ett primtal är att det endast är jämt delbart med sig själv och 1.

Sammanfattning: Ett tal är ett primtal då dess rad endast består endast av 0:or förutom för 1-kolumnen och talets egen kolumn (för kolumntal mindre än detta tal).

Ser man primtalen endast var för sig och utan sina sammasatta kompisar kan strukturen bli svår att överblicka. Ser man dem däremot inbakade på ovanstående sätt - i dessa eviga klockor som snurrar - känns det (tycker i alla fall jag) betydligt mer naturligt.


En annan klock-tabell: jämna divisioner
Här är en annan tabell som inte är lika naturlig, men som bygger på en liknande klock-princip. Här använder vi jämna divisioner enligt principen att om ett tal (raden) är jämt delbart med ett kolumntal skrivs resultatet av divisionen ut annars skrivs 0.

T.ex. division med 2 ger följande:

1 delat med 2 går inte jämt ut => 0
2 delat med 2 är 1 => 1
3 delat med 2 går inte jämt => 0
4 delat med 2 ger 2 => 2
5 delat med 2 går inte jämt => 0
6 delat med 2 ger 3 => 3
osv

Återigen ser vi en "klockeffekt" i kolumnerna:
För kolumnen 1 är det 1, 2, 3, 4, 5
För kolumnen 2 är det 0, 1, 0, 2, 0, 3
För 3 är det 0, 0, 1, 0, 0, 2, 0, 0, 3
...

Kolumnstrukturen för ett tal t: först kommer t-1 0:or sedan ett tal i konsekutivt i serien 1, 2, 3, sedan t-1 0:or, sedan nästa konsekutiva heltal etc.

Primtalen (återigen sett radvis) får vi då det endast finns 0:or på rad, förutom för kolumnerna 1 respektive t-kolumnen (dvs talets egen kolumn). Primtalen är de fetmarkerade i nedanstående tabell.


___1 2 3 4 5 6 7 8 9 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
1: 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
2: 2 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
3: 3 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
4: 4 2 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
5: 5 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
6: 6 3 2 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
7: 7 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
8: 8 4 0 2 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
9: 9 0 3 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
10: 10 5 0 0 2 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
11: 11 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
12: 12 6 4 3 0 2 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
13: 13 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
14: 14 7 0 0 0 0 2 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
15: 15 0 5 0 3 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
16: 16 8 0 4 0 0 0 2 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
17: 17 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0
18: 18 9 6 0 0 3 0 0 2 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0
19: 19 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0
20: 20 10 0 5 4 0 0 0 0 2 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0
21: 21 0 7 0 0 0 3 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0
22: 22 11 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0
23: 23 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0
24: 24 12 8 6 0 4 0 3 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0
25: 25 0 0 0 5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0
26: 26 13 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0
27: 27 0 9 0 0 0 0 0 3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0
28: 28 14 0 7 0 0 4 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0
29: 29 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0
30: 30 15 10 0 6 5 0 0 0 3 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1

Jag har för övrigt tidigare skrivit lite om diagonalerna i denna typ av tabell, se vidare
Diagonalserier.


Slutord
Återigen: Ovanstående är inget som helst matematiskt genombrott, men kanske kan det skapa något bättre förståelse kring talen.

Posted by hakank at 08:59 EM Posted to Matematik

augusti 22, 2005

IT Conversations: Stephen Wolfram

IT Conversations: Stephen Wolfram

For three centuries scientists have looked to mathematics to understand how nature works -- and to create the foundations for technology. But based on his surprising discoveries about simple computer programs, Wolfram, creator of Mathematica and author of A New Kind of Science, has developed a radically new approach. Stephen Wolfram not only addresses many fundamental questions about science and the universe, but also suggests major new directions for technology.
...

Se även
Stephen Wolfram
A New Kind of Science (Bokus, ISBN: 1579550088), som jag köpte för nästan exakt två år sedan, men har ännu inte läst hela
A New Kind of Science Online
Andra böcker av Wolfram (Bokus-länk)
Mathematica.


P.S. IT Conversations har ett gäng RSS-flöden.

Posted by hakank at 05:11 EM Posted to Komplexitet/emergens | Matematik | Systemutveckling | Comments (3)

augusti 21, 2005

Ännu mer om Persi Diaconis

"Ännu mer" i titeln hänvisar till tidigare skrivningar om Persi Diaconis. För övrigt verkar det som om det nu har länkats till lite fler av Diaconis papers på Publications.


Artikeln Maths isn't just for textbooks:

The progress of mathematics abounds in tall tales and unlikely stories. And they don't come much more improbable than this. Outside, the July sun of the Aegean is hammering down on a coastal hotel in Mykonos. Inside, America's most charismatic statistician addresses a gathering that can boast several of the world's top mathematicians as well as a motley assortment of science writers, novelists, historians and theatre people. And what is he doing? He's performing a card trick.

...

How does he do it [i.e. the card trick]? Diaconis quips that "magicians aren't allowed to explain their secrets and mathematicians can't explain their secrets". But he tries. The root of card-recognition tricks lies in the De Bruijn Sequences, a branch of what's called "combinatorics" - a discipline with a long history that stretches from the counting patterns used in Indian classical music to the coded instructions for robots used today. The mathematicians grasp the theory easily enough, but the mind-boggling mental speed of the practice still confounds them, and me.

Artikeln skriver sedan mer om hur det (roligt nog) blivit mer populärt med populärmatematik.


För övrigt 2: Di däringa De Bruijn-sekvenserna som nämns i citatet ovan kan man leka med här (som Java Applet).


(Nej, tyvärr har jag missat vartenda avsnitt av Numb3ers som nu tydligen går på svensk TV.)

Posted by hakank at 11:18 FM Posted to Matematik

Gruppteori: Konsten att fundera över hur många olika sätt man kan vända en madrass

Brian Hayes skriver i Group Theory in the Bedroom - An insomniac's guide to the curious mathematics of mattress flipping (PDF, som innehåller bilderna något mer lättåskådliga) en trevlig introducerande artikel till den matematiska disciplinen gruppteori (wikipedialänk).


En bok som täcker mer inom samma område (gruppteoretisk nöjesmatematik/nöjematematisk gruppteori) är David Joyner Adventures In Group Theory - Rubik's Cube, Merlin's Machine and Other Mathematical Toys (Bokus, ISBN: 0801869471). Ett tidigt utkast av boken finns via författarens Books-sida: SM485c lecture notes, Mathematics of the Rubik's cube (PDF).


För den som får en nyfilen eller blodad tand inom området rekommenderas det fria programpaketet GAP: GAP - Groups, Algorithms, Programming - a System for Computational Discrete Algebra.

Posted by hakank at 09:51 FM Posted to Matematik

augusti 06, 2005

Lite om konsekutiva talpar i Lotto (och dess varianter)

I Konstantinos Drakakis paper Distances between the winning numbers in Lottery (arXiv, PDF) undersöks sannolikheten för en förekomst av konsekutivt talpar i Lotto-spel. Man ger en formel för denna typ av sannolikhet, och kommer t.ex. fram till att det för ett 6/49-Lotto (dvs där 6 nummer dras av 49) är det ungefär 49.5% chans att en Lotto-rad innehåller åtminstone ett konsekutivt talpar. Vilket är förvånansvärt högt.

Här nedan är några kommentarer och utvikningar, bl.a. med hjälp av riktig data för den Lotto-form vi har i Sverige, 7/35-Lottoformen (dock ej svensk data) samt simulering av sådan Lotto-typ.


Not: Sorterad dragningslista
En not kan vara på sin plats så här i början. Det är frågan om (konsekutiva) talpar i den sorterade listan av de dragna Lotto-numren. Det gäller alltså inte talpar som uppstår i själva dragningen. Exempel: Om en dragning görs av följande "bollar" (1, 14, 34, 2, 19, 15, 20) så tittar vi här på den sorterade listan (1, 2, 14, 15, 19, 20, 34) som ha tre stycken konsekutiva talpar: (1,2), (14,15) samt (19,20).

Notera också att varken Drakakis eller jag här nedan har brytt oss om tilläggstal och andra finesser.


Matematisk formel
Problemet formuleras på följande sätt i papret:

What is the probability that, out of m > 0 numbers drawn uniformly randomly from the range 1,..., n > m, at least two are consecutive?

Dvs vad är sannolikheten att det finns minst ett konsekutivt talpar (dvs ett eller flera) om man drar m tal från intervallet 1..n.

Den slutna matematiska formeln för denna sannolikhet uträknades till

p(n,m) = 1 - p(n,m)= 1 - ( C(n-m+1, m) / C(n,m) )

där C motsvarar (binomialkoefficienten ("n över m") och som i sin tur är definierad som n!/(k!*(n-k)!). Papret visar med matematisk stringens hur man kommit fram till detta resultat, men det vågar jag inte ha någon åsikt om och kommer inte heller att beröra detta här nedan.


Konkret
Låt oss i stället bli konkreta. För den ovan nämnda Lotto-typen 6/49 studerade värdena (n=49, m=6) får man sannolikheten för att det ska finnas minst ett konsekutivt talpar om man drar 6 tal från intervallet 1..47.

I det symboliska matematisk paketet MuPad (fritt att ladda ner och fritt att använda) uttrycks det på följande sätt.

>> n:=49:m:=6:1- binomial(n-m+1,m) / binomial(n,m);float(%);

22483/45402

0.4951984494

dvs det är cirka 49.5% chans att det finns åtminstone ett talpar. Förvånande mycket, eller hur?


Simulering
Min vana trogen har jag även simulerat detta, och lika troget är det gjort i statistikpaketet R. I simuleringen gjordes 100000 "dragningar" - med sample(1:49, 6) - och sedan räknar man hur många tal som ligger intill varandra. (Som vanligt använder jag den kompakta one-liner-formen för denna typ av simuleringar. En liknande simulering har förklarats lite mer ingående här.)


> sum(sapply(1:100000, function(x) {ddd<-diff(xxx<-sort(sample(1:49,6)));sss<-sum(ddd==1);sum(sss>=1)})/100000)
[1] 0.49559

dvs 49.5%, vilket stämmer hyfsat bra med formeln.


Den svenska Lottoforme(l)n: 7/35
OK, denna typ av Lotto kanske inte är så intressant för oss. Vad med den svenska formen 7/35, dvs där man drar 7 nummer av 35? Först tar vi den teoretiska beräkningen (i MuPad):


>> n:=35:m:=7:1- binomial(n-m+1,m) / binomial(n,m);float(%);

8903/11594

0.7678971882

Dvs det är nästan 76.8% chans att det finns åtminstone ett konsekutivt talpar i de svenska lottoraderna. En simulering av 100000 dragningar ger (nästan) samma resultat 76.6%:

> sum(sapply(1:100000, function(x) {ddd<-diff(xxx<-sort(sample(1:35,7)));sss<-sum(ddd==1);sum(sss>=1)})/100000)
[1] 0.76618


Utvidningar av detta
Kommen så här långt funderade jag på några andra saker kring Lottodragningar:

- finns det data för den svenska Lotto-formen?
- hur många konsekutiva talpar finns det i genomsnitt?
- hur är fördelningen för andra typer av talpars-differenser?


Data för Lotto på formen 7/35 (dock ej svensk)
Det vore ju roligt att se hur 7/35 ser ut i praktiken. Finns det då någon lista över en massa dragningar på det detta "svenska" Lotto-format 7/35? Jepp, det finns det. Mattias Hästbacka har samlat resultaten av Lottoraderna på sin Lotto-sida. Den fullständiga listan finns på Lotto-rader från v40/1980 till v17/2005, dvs nästan 25 år.

Observera att detta inte är Svenska Spels Lottodragningar, utan motsvarande "Finska Spel". Men det spelar egentligen ingen roll för det jag vill komma åt.

Om någon har motsvarande dataanhopning för Svenska Spels Lotto så vore jag mycket intresserad av få tillgång till den. (Maila mig gärna i så fall på hakank@bonetmail.com".)

Jag har bearbetat datan och i filen lotto_all_just_numbers.txt finns "rena" rader utan någon annan information, förutom en tillbörlig källhänvisning till Mattias Hästbackas sajt.


Analys av data
OK, tillbaka till undersökningen. Det finns i Mattias Hästbackas datamängd 957 rader med åtminstone ett konsekutivt talpar av 1283 dragningar, vilket är 957/1283 = 0.746, dvs 74.6%.

Det teoretiska värdet är som vi såg ovan 76.8%, vilket skulle motsvara 1293 * 0.7678971882, dvs ungefär 985 rader. Skillnanden mellan det praktiska värdet (957) och det teoretiska (985) är 985 - 957 = 28, vilket är ett fel på 28/1283, dvs ungefär 2.2% , vilket väl får anses vara rätt hyfsat.


Hur många par blir det i genomsnitt?
Den andra frågan är något annorlunda än Drakakis ursprungliga. Hans utgångspunkt var hur stor sannolikheten är för att det ska bli ett eller flera konsekutiva talpar (dvs åtminstone ett) i en dragning. En annan fråga man kan ställa sig är: hur många konsekutiva talpar det i genomsnitt blir per dragning.

Här är den första dragningen som Mattias Hästbacka sparade (vecka 40 1980):

7, 8, 9, 16, 17, 18, 30

Det finns alltså fyra konsekutiva talpar (7,8), (8, 9), (16, 17) samt (17, 18). Så, frågan är då hur många sådana talpar det blir i genomsnitti per dragning.

En körning på Hästbackas data ger totalt 1429 konsekutiva talpar och på 1283 dragningar blir det 1429/1283 = 1.113796. Dvs för varje dragning blev det igenomsnitt 1.1 konsekutivt talbar.


Äpplen och päron
Men, kan man nu fråga sig, hur rimmar detta 1.2 talpar per dragning med att det finns 76.6% chans för att det blir åtminstone ett konsekutivt talpar per dragning? Borde sannolikheten inte bli 100% istället? Nej, det är två olika saker (olika äpplen och päron).

Konstantinos formel tar inte hänsyn hur många konsekutiva talpar det är utan endast om det är ett eller fler. Dvs det spelade ingen roll för honom om det är 1 sådant par eller 4. Denna senare uträkning tar däremot hänsyn till detta antal. Den andra skillnaden (päronet alltså) är att vi inte räknar med sannolikheter längre utan med det genomsnittliga antalet per dragning.


Fördelning av konsekutiva talpar
En fördelning av antalet konsekutiva talpar i Hästbacka-datan är

0: 325 (0.25)
1: 565 (0.44)
2: 318 (0.25)
3: 69 (0.05)
4: 4 (0.00)
5: 1 (0.00)

Dvs det finns 325 Lotto-rader utan något konsekutivt talpar (cirka 25% av alla dragningar), 565 rader med exakt 1 konsekutivt talpar (~44%) och en rad med 5 par, nämligen den 581:e dragningen (vecka 47 år 1991) som gav följande tal 15 32 33 34 35 36 37.

Låt oss nu för skoj skull simulera detta. Koden som används ser ut så här:


num.talpar = function(num.sims=1283, n=35, m=7) {
# initiera tabellen som kommer att innehåla antalet
# konsekutiva talpar. Det kan vara max m-1 (här 7-1=6) sådana talpar,
# men vi måste även ha med 0, vilket innebär att det blir m stycken
konsek.talpar = rep(0, m)
for (i in 1:num.sims) {
ss = sort(sample(1:n, m))
dd = diff(ss) # differensen mellan talen
tt = sum(dd==1) # hur många konsekutiva talpar finns det
# öka med 1. Not: "tt+1" är för att även få med dragninar som
# inte har något konsekutivt talpar
konsek.talpar[tt+1] = konsek.talpar[tt+1] + 1
}
return(konsek.talpar)
}


Här är en sådan körning som har värden som inte är helt olika de faktiska (dvs Hästbacka-datan). Först antal och sedan fördelningen.

> (ss = num.talpar(1283))
[1] 314 519 353 88 8 0

> round(ss/1283,2)
[1] 0.24 0.40 0.28 0.07 0.01 0.00

För just denna simulering blev det alltså cirka 314 dragningar (cirka 24%, av 1283 rader) utan något konsekutivt talpar alls, 519 dragningar med ett sådant talbar, och hela 8 dragningar med 5 k.t.p (dvs där det finns 6 konsekutiva tal).

Om vi nu brassar på med 100 sådana här simuleringar om vardera 1283 dragningar, dvs 1283*100 = 128300 dragningar (och delar de värden vi får med 100) så får vi något mer exakta värden att jämföra med:


> (ss=num.talpar(1283*100)/100)
[1] 299.31 540.63 339.48 92.53 10.60 0.45 0.00

> round(ss/1283,2)
[1] 0.23 0.42 0.26 0.07 0.01 0.00 0.00

Vi ser alltså att det finns cirka 23% chans att det blir 0 stycken k.t.p., cirka 42% att det blir exakt ett k.t.p. osv.

Den intressanta frågan blir då vad är det (simulerade) genomsnittet konkekutiva par per dragning. I faktisk data blev det cirka 1.1 konsekutivt par per dragning.


sum.talpar = function(num.sims=1283, n=35, m=7) {
antal.talpar = 0
for (i in 1:num.sims) {
ss = sort(sample(1:n, m))
dd = diff(ss) # differensen mellan talen
tt = sum(dd==1) # hur många konsekutiva talpar finns det
antal.talpar = antal.talpar + tt
}
return(antal.talpar)
}
sum.talpar()


Först en enkel körning för att få en känsla för informationen.

> ss = sum.talpar(1283)
[1] 1580

> ss/1283
[1] 1.231489

Och sedan en lite tyngre körning


> sum.talpar(1283*100)/(1283*100)
[1] 1.200514

Dvs det blir cirka 1.2 konsekutiva talpar per dragning. Det är alltså mer än ett par i genomsnitt.

Hur fördelas differenserna av talen?
Ovan har vi endast studerat konsekutiva talpar, dvs tal där differensen är 1. Nen det är även intressant att studera övriga differenser som uppkommit i dragningarna. Det vi ovan kallat för "konsekutiva talpar" är talpar med differensen 1, vilket vi i det följande kallar "1-differens".

I Hästbacka-datan fördelas sig differenserna enligt följande (på formatet differens: antal förekomster). Notera att en dragning nästan alltid har flera olika differenser. T.ex. ovanstående 5-talpars-dragning (15 32 33 34 35 36 37) har fem stycken 1-differenser samt en 17-differens (dvs 32 - 15 = 17).

1: 1429
2: 1184
3: 939
4: 790
5: 683
6: 585
7: 447
8: 345
9: 283
10: 231
11: 207
12: 126
13: 108
14: 99
15: 66
16: 48
17: 44
18: 17
19: 22
20: 11
21: 16
22: 2
23: 5
24: 2
25: 3

Man kan här se att det är flest 1-differenser, sedan blir det ständigt färre och färre.


OK, för fullständighets skull så simulerar vi även detta. Koden är rätt lik den föregående.

diff.table.sim = function(num.sims=1283, n=35, m=7) {
diff.table = rep(0, n)
for (i in 1:num.sims) {
ss = sort(sample(1:n, m))
dd = diff(ss) # differensen mellan talen
# lägg in respektive differens i tabellen
for (d in dd) {
diff.table[d] = diff.table[d] + 1
}
}
return(diff.table)
}

Det vi söker är alltså det genomsnittliga antalet differens per dragning, så vi simulerar 100000 dragningar.

> cbind(diff.table.sim(100000)/100000)
[,1]
[1,] 1.19969
[2,] 0.98629
[3,] 0.80547
[4,] 0.65678
[5,] 0.52912
[6,] 0.42424
[7,] 0.33684
[8,] 0.26439
[9,] 0.20978
[10,] 0.15981
[11,] 0.12235
[12,] 0.09001
[13,] 0.06614
[14,] 0.04662
[15,] 0.03512
[16,] 0.02358
[17,] 0.01583
[18,] 0.01097
[19,] 0.00734
[20,] 0.00406
[21,] 0.00281
[22,] 0.00149
[23,] 0.00073
[24,] 0.00033
[25,] 0.00013
[26,] 0.00006
[27,] 0.00002
[28,] 0.00000
[29,] 0.00000
[30,] 0.00000
[31,] 0.00000
[32,] 0.00000
[33,] 0.00000
[34,] 0.00000
[35,] 0.00000

Varvid vi kan se att det är i genomsnitt (nästan) 1.2 stycken 1-differenser (dvs det vi ovan kallade konsekutiva talpar) per dragning, i genomsnitt 0.99 2-differens per rad osv.


Genomsnittlig antal differenser
Det genomsnittliga antalet differenser är cirka 4.53 enligt följande simulering. Här delas summan av differensvärdena med det totala antalet uppkomna differenser. (Man kan trixa med föregående värden, men jag vill ha lite kontroll över saker och ting.)

diffs = function(num.sims=1283, n=35, m=7) {
diffs = 0
num.diffs = 0
for (i in 1:num.sims) {
ss = sort(sample(1:n, m))
dd = diff(ss)
for (d in dd) {
diffs = diffs + d
num.diffs = num.diffs + 1
}
}
m = diffs/num.diffs # genomsnittligt antal
return(c(diffs, num.diffs, m))
}

Och så körningen, där vi endast är intresserade av det sista värdet:


> round(diffs(1283*100),3)
[1] 3465204.000 769800.000 4.501

Vilket alltså ger det genomsnittliga differensvärdet 4.501. Äh, vi säger 4.5.


Sammanfattning
Här ovan har vi kommit fram till bl.a. följande:

* Sannolikheten att det ska förekomma åtminstone ett konsekutivt talpar i en 7/35-dragning är cirka 77%
* Det blir i genomsnitt 1.2 konsekutiva talpar per dragning.
* Det genomsnittliga differensvärdet för en dragning är 4.5.

Som antytts så anser i alla fall jag att det är förvånande.

Upprinnelse (inspiration)
Upprinnelsen till allt detta var notisen Consecutive pairs in winning lottery numbers hos MathForge.


Se även
Se även min genomgång av födelseparadoxen,tillika med R-kod, i Sammanträffanden - anteckningar vid läsning av Diaconis och Mosteller 'Methods for Studying Coincidences'.

Jämför även med den simulering som gjordes för ett liknande problem (6/49-Lotto) i Lite om resampling, simulering, sannolikhetsproblem etc.. Sök efter "Litet problem i (engelsk) Lotto". (Det koms dock inte fram till exakt samma sak.)

Samt överhuvudtaget Simulation, probability theory etc, såsom Trisssimuleringen (Java applet).

Posted by hakank at 03:37 EM Posted to Matematik | Statistik/data-analys | Comments (8)

juli 31, 2005

Augusti-pyssel

Så här på mina andra semesterdag (eller dagen före första semesterdagen beroende på hur man räknar) bör det passa med lite semester-pyssel.


(2005-08-05: Uppdaterade giltighetstiden för öl/glassbjudandet i utbyte mot gåtans lösning från ett dygn till en månad. För det första var det ett för ogeneröst tilltaget erbjudande, för det andra verkar det vara svårare än jag trodde, och för det tredje så kanske inte så många ännu har försökt lösa det av olika skäl. För övrigt kan jag tänka mig att fråga 2 kommer att väcka vissa protester, eller möjligen suckar. Se det som ytterligare en ledtråd.)


Som vanligt när det gäller denna typ av pysslar kan det finnas flera lösningar. Här nedan har jag tänkt på en speciell lösning (normalt en "enkel" och "naturlig" lösning även om enkelheten kanske först kommer då lösningen har kommits på eller presenterats. Cf Asplund.), och det är den som räknas som korrekt. Andra lösningar som är lika enkla/naturliga (eller ännu mer dito, eller för den delen mer sökta men kreativa) premieras med ett eller flera "wow! coolt!".

Det utdelas inga fina priser, men om någon löser samtliga problem inom ett dygn en månad (dvs fram till 1 augusti 1 september 2005, klockan 12.00, normalsvensk tid) samt meddelar mig de korrekta lösningarna innan någon annan hunnit före, kommer jag att bjuda på en öl/glass nästa gång vi träffas (t.ex. i anslutning till Bloggforum 3, fast då är glass troligen inte så populärt). ("Korrekta" i betydelsen ovan alltså, alternativt synnerligen kreativa varianter med en lika synnerlig subjektiv - av mig - bedömning av vad som är kreativt.)

Jag förbehåller mig dock rätten att bjuda en person på öl och/eller glass enligt eget gottfinnande även om denne inte uppfyllt de ovan nämnda villkoren eller ens försökt att lösa pysslen, eller ens är medveten om dess existens.

Notera också att jag inte här värdesätter pyssellösningsära till en simpel öl eller glass, utan det ska endast ses som symboliskt erkännande av en fin bedrift.

Eventuellt kommer det efterhand (men tidsligt ospecificerat) att ges lite ledtrådar.


Lycka till!

Pysslarna

1) Vad står här egentligen och varför (dvs enligt vilken metod): 1045668080


2) Vad står här egentligen och varför: 15604225


3) Vad ska stå i stället för "?" i nedanstående?

a) ...., 1596, ?
b) ...., 78, ?
c) ...., 129, ?

Not1: Det kan vara olika svar i respektive fråga, men det kan också vara samma svar.

Not2: Antalet "."-er bör inte ge någon ledtråd till lösningen.


4) Vad är det gemensamma för nedanstående ord?

* besökes
* eksem
* gömmes
* webb

Lösningen ska ge en ledtråd till en av de ovanstående spörsmålen i 1) till 3). Mer specifik: ger det ingen ledtråd är det troligen inte den korrekta lösningen.

Not: Det finns andra svenska ord som är lika gemensamm som dessa.

Posted by hakank at 10:51 FM Posted to Matematik | Comments (2)

juli 22, 2005

Math Matters videoföreläsningar

Som tidigare skrivits tycker jag om videoföreläsningar i matematisk kopplade ämnen (och naturligtvis även andra ämnen i intressesfären). Via MathForge hittades idag Math Matters IMA Public Lecture Series.

Där finns t.ex.
* James D Murray: The Marriage Equation - A Practical Theory for Predicting Divorce and a Scientifically-Based Marital Therapy, den teori om olika typer av giftermål som Murray beskriver i boken Mathematics Of Marriage - Dynamic Nonlinear Models (Bokus, ISBN: 0262572303) skriven tillsammans med John M Gottman (Gottman står som huvudförfattare). Murray har också ett kapitel om detta i sin Mathematical Biology - Spatial Models and Biomedical Applications (Bokus, ISBN: 0387952284). Malcolm Gladwell skrev också en del om teorin i sin Blink (Bokus, ISBN: 0316001058. Cf t.ex. min recension av denna bok.)

* Steven Strogatz: Sync: The Emerging Science of Spontaneous Order. Strogatz har skrivit en intressant populärvetenskaplig bok om just detta Sync (Bokus, ISBN: 0786887214) - som jag märkligt nog inte recenserat men rekommenderar storligen - men framförallt skrivit den fantastiska läroboken om dynamiska system Nonlinear Dynamics and Chaos - With Applications to Physics, Biology, Chemistry and Engineering (Bokus, ISBN: 0738204536). Se även kategorierna Komplexitets/emergens och Social network analysis/complex networks där Strogatz nämns från tid till annan. I föreläsningen får man bl.a. se den eldflugors synkronisering, ett fenomen som väl kan ses som paradigmfallet av synkronisering och var det som fick Strogatz (tillsamman med Duncan Watts) att studera komplexa nätverk.

* Benoit Mandelbrot: Fractals/Multifractals in Finance, the Internet & Other "Wild" Aspects of Man's Works

* Richard A. Tapia: Math at Top Speed: Breaking Myths in the Drag Racing Folklore

* Bruce Schneier: Natural Laws of Digital Content: the Folly of Copy Protection on the Internet


Se även Recordings of IMA Talks som innehåller ett flertal föreläsningar i diverse ämnen, vad jag kan se inte alls lika populariserande hållna.

I samma anda kan här rekommenderas MIT:s OpenCourseWare som har vissa videoföreläsningar, bl.a. den som just nu tar upp en hel del av min tid: Differential Equations med föreläsaren Arthus Mattuck.

Posted by hakank at 07:33 FM Posted to Agentbaserad modellering | Komplexitet/emergens | Matematik | Social Network Analysis/Complex Networks

juli 12, 2005

Skoj förströelse: Planarity

Förströelsen Planarity (kräver Flash) går ut på att man ska se till så att inga linjer korsar varandra.

"Planarity" (planaritet) är en egenskap hos en graf som innebär att man kan rita den (på ett plan) så att inga linjer korsas. Se mer i Wikipedias planar (en.wikipedia) samt MathWorlds PlanarGraph.

Här finns lite diskussioner om bästa metoden. Möjligen kan man även få lite tips från forskningen kring Graph Drawing (stor fet PDF-fil från graphdrawing.org).


Uppdatering
Det finns en liten diskussion på Crooked Timber: Untangle the dots.

Uppdatering 2
Det har kommit upp en FAQ (på samma sida som spelet).

Nu börjar det skrivas lite längre artiklar (OK då, kanske inte så långa) om John Tantalo, skaparen av programmet:
Case Student Invents Hit Online Game- Programmer Gets Idea From Girlfriend.
Från universitet där Tantalo går: Case student develops booming on-line game

Posted by hakank at 09:10 EM Posted to Matematik | Comments (3)

juni 21, 2005

Ivars Peterson: Sudoku Math

Jag har - möjligen märkligt nog - inte blivit så tagen av Sudoku som flera av mina vänner. Det kanske kommer.

Ivars Peterson har hur som helst skrivit lite om matematiken bakom Sudoku i sin Math Track Sudoku Math.


Se även
Wikipedia: Sudoku
Åtminstone två svenska tidningar har återkommande Sudokus:
Sydsvenskan
Svenska Dagbladet


(En personlig association: Inte heller korsord har intresserat mig speciellt systematiskt. Något som jag däremot tyckte var väldigt roligt var de där Krypto-korsorden som såg ut som ett vanligt korsord men det fanns inga ledtrådar. I stället var varje ruta numrerad och några få rutor hade bokstäverna redan ifyllda. Man skulle så lista ut vilka bokstäver som motsvarade vilka tal. Hmm, det kanske finns sådant online.)

Posted by hakank at 07:06 FM Posted to Matematik | Comments (2)

juni 20, 2005

Grävlingsserien

Not: Denna anteckning har en begränsad men - sedd i efterhand - synnerligen väldefinierad målgrupp.


Följande fråga ställes: Om en grävling får 4 st barn hur många blir de tillsammans?

Efter några inledande tveksamheter och pannvecklande samt ytterligare två koppar te kan olika svar förevisas.

a) Det är 5 grävlingar eftersom 1 + 4 = 5.


b) Svaret kan bero på vem som är "givaren". Eller snarare: Eftersom det oftast krävs två grävlingar för att skapa ett grävlingsbarn innebär det att det är 2 föräldrar samt 4 barn, dvs totalt 6 grävlingar.


b2) Å andra sidan kanske det krävs n grävlingar för att skapa ett grävlingsbarn där svaret i så fall är: 1 + 4 + n = 5 + n grävlingar.


c) Grävlingsserien
Om det inte finns något uttryckligt villkor för summeringens slut skulle det bli en regress (i princip oändlig, eller i alla fall tills pappret, internminne eller samtliga atomer i universum har tagits i anspråk för anteckningarna). Denna serie ska här nedan avtäckas.

Några underförstådda förutsättningar:
- en (1) grävling får exakt 4 (fyra) ungar, varken fler eller färre
- inga grävlingar dör i denna värld
- det är en lustig värld som här framträder
- vi bryr oss inte det minsta om varifrån den första grävlingen kommer. Den bara finns där och har förmåga att skapa (exakt) 4 barn.


Först finns det alltså en enda grävling: Totalt 1 grävling.
Sedan får denna grävling fyra ungar: Totalt 1 + 4 = 5 grävlingar.

Dessa 4 grävlingar får respektive 4 ungar = 16,
Totalt är detta 1 + 4 + 16 = 21 grävlingar

Dessa 16 grävlingsbarn får respektive 16 * 4 = 64 barn, och totalt blir detta 1 + (1*4) + (4*4) + (16*4) = 1 + 4 + 16 + 64 = 85 grävlingar. Osv.

Serien definieras enligt följande rekursionsformel där G[g] är hur många grävlingar det finns vid generationen g (g = 0..stort tal).

G[0] = 1
G[g] = Sum(G[i],i = 1..g-1) + 4 * G[g-1]

dvs antalet grävlingar (G) i "denna" generation definieras av summan av de grävlingarna i de tidigare generationerna plus antalet barn som föddes i den föregående generationen.

Vilket här ger följande serie:

1, 5, 21, 85, 341, 1365, 5461, 21845, 87381, 349525, ...

Antal barn som föds i respektive generation är (vi antog att den första grävling magiskt uppstått ur intet eller något sådant).

(1), 4, 16, 64, 256, 1024, 4096, 16384, 65536, 262144, ...

vilket enkelt kan uttryckas som

4^g för g=0..samma stora tal

Grävlingsserien har den genererande funktionen:

- 1
--------------------
( -1 + 5*x - 4*x^2 )

En generalisering av denna funktion är att antal barn per grävling blir variabel (betecknas med N) vilket då ger den genererande funktionen:

- 1
------------------------
( -1 + (N+1)*x - N*x^2 )

T.ex. om en grävling får 10 barn (N = 10) blir det följande grävlingsserie:

1, 11, 111, 1111, 11111, 111111, 1111111, 11111111, 111111111, 1111111111, ...

Detta är inte är så konstigt eftersom antal grävlingar som föds i respektive generation är:

1, 10, 100, 1000, 10000, 100000, 1000000, 10000000, 100000000, 1000000000, 10000000000, ...

Ja, det var alltså Grävlingsserien.


d) Om du just nu sitter på SommarHacket och undrar vad denna fråga leder så har du kommit rätt och skall ange bokstaven K som svar, men inte annars.


e) Det finns med stor sannolikhet fler alternativa svar på frågan som ställdes. T.ex. 4.


Man skulle även kunna tolka allt det ovanstående enligt följande substitutionsregel:
Grävling = Gåta.
Får X barn = Inspirerar till ytterligare X gåtor.


Se även
Cut The Knot: Generating functions
The On-Line Encyclopedia of Integer Sequences.

Posted by hakank at 07:38 EM Posted to Matematik | Comments (7)

juni 13, 2005

Ivars Peterson: En matematisk analys av tennis

Ivars Peterson skriver i MathTrek : Winning at Tennis om matematisk och statistisk analys av tennis:

In the April Studies in Applied Mathematics, Paul K. Newton of the University of Southern California and Joseph B. Keller of Stanford University provide formulas for computing a tennis player's chances of winning and, in effect, for predicting the outcome of tennis tournaments. In the context of their model, Newton and Keller also prove that the probability of winning a set or match doesn't depend on which player serves first.

It isn't enough to know just the rankings of the two players in a tennis match. There's no obvious, unambiguous way to translate a ranking into a probability of winning. Instead, it turns out that the key factor is the probability that each player wins a rally against the other player when he or she serves. Typically, you assume that these probabilities stay the same throughout a match.

Referenser till gjord forskning finns i artikeln, vilken se. Tyvärr är många artiklar inte publikt tillgängliga.


Se även Ivars Petersons tidigare MathTrek

Posted by hakank at 07:55 EM Posted to Matematik | Sport, idrott, hälsa | Statistik/data-analys | Comments (1)

juni 06, 2005

John Allen Paulos: What Numbers Reveal -- from Sumo Wrestlers to Professors

Inte helt förvånande skriver John Allen Paulos om boken Freakonomics: What Numbers Reveal -- from Sumo Wrestlers to Professors:

Looking at large data sets and deriving loud conclusions from the reams of whispering numbers is often enjoyable. Herein are three quite disparate examples.

The first concerns Sumo wrestlers and comes from Freakonomics, a fascinating new book by economist Steven Levitt and writer Stephen Dubner, that employs Levitt's quirky economic insights to illuminate many everyday activities and practices. The second is simply a study I reported on in a book I wrote on the stock market, and the third comes from a simple analysis I recently made of grade distributions for a required math course at my university.


Se även
Tidigare anteckningar (google) om Paulos
Recension av boken Freakonomics Steven D. Levitt, Stephen J. Dubner: Freakonomics : A Rogue Economist Explores the Hidden Side of Everything

Posted by hakank at 12:56 EM Posted to Matematik | Statistik/data-analys

mars 15, 2005

Jordan Ellenberg: Does Gödel Matter? - The romantic's favorite mathematician didn't prove what you think he did

Jordan Ellenberg: Does Gödel Matter? - The romantic's favorite mathematician didn't prove what you think he did. är en recension av Rebecca Goldsteins bok Incompleteness: The Proof and Paradox of Kurt Godel.

In his recent New York Times review of Incompleteness, Edward Rothstein wrote that it's "difficult to overstate the impact of Gödel's theorem." But actually, it's easy to overstate it: Goldstein does it when she likens the impact of Gödel's incompleteness theorem to that of relativity and quantum mechanics and calls him "the most famous mathematician that you have most likely never heard of." But what's most startling about Gödel's theorem, given its conceptual importance, is not how much it's changed mathematics, but how little. No theoretical physicist could start a career today without a thorough understanding of Einstein's and Heisenberg's contributions. But most pure mathematicians can easily go through life with only a vague acquaintance with Gödel's work.

Posted by hakank at 05:46 EM Posted to Matematik | Comments (8)

februari 06, 2005

Philip Ball: Freudian quips (om matematikers humor)

I Nature-artikeln Freudian quips skriver Philip Ball om matematikers humor.

If, therefore, Freud was right to claim that jokes relieve anxiety by releasing suppressed feelings, mathematicians' jokes betray a deep-seated worry about whether their proofs are, so to speak, big enough. A humorous 'guide for lecturers' outlines the many different kinds of proof available.

Papret som refereras till i artikeln är
Paul Renteln, Alan Dundes: Foolproof: A Sampling of Mathematical Folk Humor (PDF).


Se även
Några böcker om vitsar med anledning av en The New Yorker-artikel
Vad är en vits?

Posted by hakank at 12:16 EM Posted to Diverse vetenskap | Humor | Matematik | Comments (3)

november 21, 2004

MSRI Math Lectures

Under en liten mail-diskussion med Bengt (Frihetens Vingar) om hans e-learning-sajt Edulink - Eway to learning kom jag att tänka en sajt som jag hittade för flera år sedan och blev väldigt fascinerad av: MSRI Streaming Video (MSRI: Mathematical Sciences Research Institute) där det finns mängder av videoföreläsningar kring matematik, statistik och dess applikationer i olika områden. Även om matten oftast är way over my head är det roligt att se dessa föredrag (och ha möjlighet att se dem om man skulle bli mer insatt i ett ämne).

Nu vet jag inte om rena videoföreläsningar egentligen tillhör e-learning-begreppet, men kul är det i alla fall.

Numera finns (en del av) dessa föreläsningar även på Internet Archive (www.archive.org): Internet Archive: MSRI Math Lectures.

Där finns även en lista över de mest populära föresläsningarna, t.ex.
Fun with Mathematics: Some Thoughts from Seven Decades
Fermat's Last Theorem - The Theorem and Its Proof: An Exploration of Issues and Ideas
Introduction to Quantum Computing

Posted by hakank at 08:58 FM Posted to Matematik | Comments (2)

oktober 10, 2004

Terrorism och matematik

AP-artikeln Mathematicians Offer Help in Terror Fight berättar om ett gäng matematiker och andra som samlades för att diskutera terrorism:

A small group of thinking men and women convened at Rutgers University last month to consider how order theory — a branch of abstract mathematics that deals with hierarchical relationships — could be applied to the war on terror.

Troligen är det DIMACS Workshop on Applications of Order Theory to Homeland Defense and Computer Security som avses. Se Abstracts samt Important links.

Artikeln nämner bland annat matematikern Jonathan David Farley :
Mathematician Jonathan Farley of the Massachusetts Institute of Technology [...] said he was inspired to organize the meeting by the movie "A Beautiful Mind." The film tells the story of mathematician John Forbes Nash, whose work in game theory found application in Cold War military strategy, international trade and the auctioning of broadcast frequencies by the Federal Communications Commission [...].

Farley har t.ex. skrivit Breaking Al Qaeda Cells: A Mathematical Analysis of Counterterrorism Operations (A Guide for Risk Assessment and Decision Making) (PDF).


Övriga länkar:
Ivars Peterson Splitting Terrorist Cells
Order theory

Posted by hakank at 08:33 FM Posted to Matematik

oktober 08, 2004

Mer om myntsingling

I Diaconis om myntsingling skrevs om en undersökning som Persi Diaconis, Susan Holmes och Richard Montgomery gjort kring myntsingling.

Nyss stötte jag på deras paper om detta: Dynamical Bias in the Coin Toss (PDF)
Abstract:
We analyze the natural process of flipping a coin which is caught in the hand. We prove that vigorously-flipped coins are biased to come up the same way they started. The amount of bias depends on a single parameter, the angle between the normal to the coin and the angular momentum vector. Measurements of this parameter based
on high-speed photography are reported. For natural flips, the chance of coming up as started is about .51.

Det visas också några fina bilder på mojängen som användes.

Posted by hakank at 11:58 EM Posted to Matematik

de Bruijn-sekvenser (portkodsproblemet)

Tänk att du har glömt din portkod och ska försöka testa alla möjligheter men vill knappa in så få siffror som möjligt. Hur ska du gå tillväga? Förutsättningen är att portkoden har fyra siffror (0-9) och att man inte behöver trycka "Enter" eller liknande efter varje sekvens som testas, dvs det är bara att knappa på tills rätt sekvens slagits in.

För något år sedan var jag intresserad av just detta problem och skrev två program för att få fram denna typ av sekvenser som alltså kallas för de Bruijn-sekvenser: Ett CGI-program som har en rätt kraftig restriktion av hur stora sekvenserna kan vara, och en Java-applet utan några sådana begränsningar. Här visas en lösning på ovanstående problem.


Stefan Geens skrev idag en lång och fascinerande exposé över detta problem i The de Bruijn code, där han bl.a. var vänlig nog att länka till ett av dessa program. Han förklarar naturligtvis allting mer och bättre.

För fullständighetens skull refereras åter till källorna:
Mathworld: de Bruijn sequence
The (Combinatorial) Object Server: Information on necklaces, unlabelled necklaces, Lyndon words, De Bruijn sequences där jag fick tag i den algoritmen som används i programmen.

Posted by hakank at 10:15 EM Posted to Matematik | Comments (1)

augusti 01, 2004

Erich Friedman: Matematisk pyssel

Erich Friedman har en hel del sidor med matematiskt pyssel.

Såsom:
Math Magic (se även länkarna sist på den sidan)
Math Magic Archives
Puzzle Palace
Ambigrams
Mathematical Horoscope
Friedman number
Top Ten Lists (som innehåller även annat än matematik).

Posted by hakank at 08:40 EM Posted to Matematik | Comments (2)

juli 29, 2004

Matematik och berättande

EurekAlert!: UW researcher links storytelling and mathematical ability

Math and storytelling may seem like very different abilities, but a new study by University of Waterloo scientist Daniela O'Neill suggests that preschool children's early storytelling abilities are predictive of their mathematical ability two years later.
...
This study suggests that building strong storytelling skills early in the preschool years may be helpful in preparing children for learning mathematics when they enter school.


Se även
Daniela O'Neill
University of Waterloo's Centre for Child Studies

Posted by hakank at 11:18 EM Posted to Matematik

juli 13, 2004

Google Blog om Google-jobb-gåtan

I fredags tipsade Erik Stattin om Googles jobbgåta: Geekiga jobbannonser.

Google Blog skriver (idag/i går) om den i Warning: We Brake For Number Theory, där bl.a. den berömda skylten visas.

Man kan notera att lösningen har funnits ute på nätet sedan i fredags. I söndags kunde man den hittas via google. Tyvärr är svaret inte 42.

Posted by hakank at 07:44 FM Posted to Matematik | Comments (1)

juli 06, 2004

e

John Allen Paulos: Now Featuring ‘e’: Pi and Phi Have Been in the Spotlight. What about e?

Specific numbers sometimes play a role in fiction. Witness the novel The Da Vinci Code, where the number is the Golden Ratio symbolized by the Greek letter phi, or the movie Pi, where the number is pi, of course.
...
Reflecting on the use of these numbers in fiction, I wondered how a number that doesn't get as much attention as phi or pi might serve as a plot element in a mystery. The number does not have a Greek name, but must make do with a simple moniker — e. The base of the natural logarithm and truly one of the most important numbers in all of mathematics, e is approximately 2.71828182845904 … (approximately because its decimal expansion continues without repetition).

Och sedan kommer några förslag till filmplottar kring e .


Några noter:
Det finns en trevlig bok om e: e: The Story of a Number
MathWorld: e
The constant e and its computation
Robert Matthews och pi på himlavalvet: Pi in the sky (abstract för artikeln Nature 374 681-682, 1995).

Posted by hakank at 06:38 FM Posted to Matematik

juni 09, 2004

Mer om Persi Diaconis

I Stanford Report-artikeln Lifelong debunker takes on arbiter of neutral choices skrivs lite mer om Persi Diaconis forskning och bakgrund.

Se även t.ex. Persi Diaconis videoföreläsning "On Coincidences" (1998).


Posted by hakank at 07:01 FM Posted to Husgudar | Matematik | Skepticism, parapsykologi etc

juni 07, 2004

Axiom (Computer Algebra System)

Axiom är ett system för datoralgebra (Computer Algebra Systems), som tidigare varit kommersiellt, men nu har släppts ganska fritt (läs licenserna noga).

Axiom is a general purpose Computer Algebra system. It is useful for research and development of mathematical algorithms. It defines a strongly typed, mathematically correct type hierarchy. It has a programming language and a built-in compiler.

Axiom has been in development since 1971. At that time, it was called Scratchpad. Scratchpad was a large, general purpose computer algebra system that was originally developed by IBM under the direction of Richard Jenks. The project started in 1971 and evolved slowly. Barry Trager was key to the technical direction of the project. Scratchpad developed over a 20 year stretch and was basically considered as a research platform for developing new ideas in computational mathematics. In the 1990s, as IBM's fortunes slid, the Scratchpad project was renamed to Axiom, sold to the Numerical Algorithms Group (NAG) in England and became a commercial system. As part of the Scratchpad project at IBM in Yorktown Tim Daly worked on all aspects of the system and eventually helped transfer the product to NAG. For a variety of reasons it never became a financial success and NAG withdrew it from the market in October, 2001.

NAG agreed to release Axiom as free software. The basic motivation was that Axiom represents something different from other programs in a lot of ways. Primarily because of its foundation in mathematics the Axiom system will potentially be useful 30 years from now. In its current state it represents about 30 years and 300 man-years of research work. To strive to keep such a large collection of knowledge alive seems a worthwhile goal.


Det finns även binär version av Axiom för Linux att ladda ner från denna sida. Den binära versionen funkade inte inte hos mig, så jag hämtade den senaste källkoden från CVS:en och kompilerade koden. Det tog cirka 6 timmar här hemma, och blev totalt över 500Mb. Men det funkar.

Axiom påminner rätt mycket om MuPAD, vilket också bör kollas in av den som känner sig lockad av kostnadslösa datoralgebrasystem. Men det är svårt att konkurrera med Maple och Mathematica.

Specifika nyhetsgrupper för Axiom:
axiom-developer
axiom-mail
axiom-math

Det finns också en bok (PDF, cirka 3Mb) på över 1100 sidor som beskriver systemet. Motsvarade DVI-fil skapas automatiskt vid kompileringen.

(Via Lambda The Ultimate.)

Posted by hakank at 08:22 EM Posted to Matematik

juni 04, 2004

Röstning och matematik

Som gammal statsvetare med intresse för matematik blev jag intresserad av Ny Teknik-artikeln EU rättvisare med kvadratrötter (publicerad för några dagar sedan): EUs röstregler är både irrationella och orättvisa, menar två polska fysiker. Men rättvisan kan återställas med hjälp av kvadratrötter, föreslår de.
...
Genom att ha ett röstetal som är proportionell mot kvadratroten ur antalet medborgare i landet får alla européer lika mycket att säga till om, oberoende av om de bor i Tyskland eller Malta.

Forskarnas namn är med större sannolikhet Karol Zyczkowski samt Wojciech Slomczynski snarare än de som står i artikeln. Efter lite letande hittades ett paper (PDF) av dessa författare som verkar vara relevant:

Voting in the European Union : The square root system of Penrose system and critical point
Abstract: The notion of the voting power is illustrated by examples of the systems of voting in the European Council according to the Treaty of Nice and the more recent proposition of the European Convent. We show that both systems are not representative, in a sense that citizens of different countries have not the same influence for the decision taken by the Council. We present a compromise solution based on the law of Penrose, which states that the weights for each country should be proportional to the square root of its population. Analysing the behaviour of the voting power as a function of the quota we discover a critical point, which allows us to propose the value of the quota to be 62%. The system proposed is simple (only one criterion), representative, transparent, effective and objective: it is based on a statistical approach and does not favour nor handicap any European country.

Möjligen kan följande av samma författare också vara intressant:
Rules Governing Voting in the EU Council.

Posted by hakank at 08:17 EM Posted to Matematik

maj 29, 2004

Primtalstvillingar

Richard Arenstorf ger sig på att bevisa att det finns oändligt antal primtalstvillingar: There Are Infinitely Many Prime Twins.
Abstract
A proof of the twin-prime conjecture is presented using methods from classical analytic number theory.

Se vidare Mathworld-artiklarna
Twin Prime Conjecture
TwinPrimes.

Via en slashdotdiskussion av sedvanlig kvalitet.

(Nej, jag har inte läst och förstått papret.)

Posted by hakank at 07:40 FM Posted to Matematik

april 09, 2004

Bloom-filter

Perl.com-artikeln Using Bloom Filters, skriven av Maciej Ceglowski (bloggar Idle Words) förklarar Bloom-filter samt visar hur man använder Bloom-filter i Perl samt har ett flertal länkar till vidare dokumentation.


Först förklaras principen med Bloom-filter och jämför med en enkel (brute force) uppslagning i hashtabell.

Many people don't realize that there is an elegant alternative to the lookup hash, in the form of a venerable algorithm called a Bloom filter. Bloom filters allow you to perform membership tests in just a fraction of the memory you'd need to store a full list of keys, so you can avoid the performance hit of having to use a disk or database to do your lookups. As you might suspect, the savings in space comes at a price: you run an adjustable risk of false positives, and you can't remove a key from a filter once you've added it in. But in the many cases where those constraints are acceptable, a Bloom filter can make a useful tool.

En av användningarna av dessa filter är inom sociala nätverk (artificiella sociala nätverk eller distribuerade sociala protokoll såsom FOAF, Friends Of A Friend) för att verifiera användare. Denna teknik används i LOAF, det spamfilterprogram som Maciej Ceglowski skrivit tillsammans med Joshua Schachte, skapare av bl.a. memepool, del.icio.us samt GeoURL.


One drawback of existing social network schemes is that they require participants to either divulge their list of contacts to a central server (Orkut, Friendster) or publish it to the public Internet (FOAF), in both cases sacrificing a great deal of privacy. By exchanging Bloom filters instead of explicit lists of contacts, users can participate in social networking experiments without having to admit to the world who their friends are. A Bloom filter encoding someone's contact information can be checked to see whether it contains a given name or email address, but it can't be coerced into revealing the full list of keys that were used to build it. It's even possible to turn the false-positive rate, which may not sound like a feature, into a powerful tool.


Se även
På About LOAF beskrivs programmet, länk för nedladdning av program. Notera även beskrivninarna av attacker på sociala nätverk.

Posted by hakank at 11:42 FM Posted to Matematik | Social Network Analysis/Complex Networks

april 04, 2004

Puzzles + Math = Magic

New York Times: Puzzles + Math = Magic

...
In the case of Mr. Ganson's machine, the wonder is at how complicated a mechanism was required to do something so apparently simple, in Mr. MacCready's at how simple a solution was needed to accomplish something usually so complicated.

In both, though, the wonder is how something is done. Magicians are also inventors, but spur astonishment not at how something is done — though that is always the question asked — but that it is done at all.

At one performance, the magician Jamy Ian Swiss asked an audience member to come onstage and close her eyes. He promised he would pass a wire hanger through her body without her feeling it. But he let the audience see precisely how the trick was done. The audience laughed at the trick's obviousness, but she, having seen nothing, was amazed. "Now which of you," the magician asked, "has had the better experience?"

The mathematician and puzzler dissent, of course, insisting that the best experience is in knowing. The goal is not illusion, but disillusion. See the coffee cup as a mechanism with magnets, show the palmed cards, explain why certain series of numbers act in a certain way.
...
As the mathematician Peter Winkler said in one talk: "No matter how simple something is, there's room for it to be too hard to do."

Posted by hakank at 06:34 EM Posted to Matematik

februari 16, 2004

Giftermålets matematik

Nature: Maths predicts chance of divorce:
Ignoring snide comments and stopping yourself from rolling your eyes at the stupidity of your partner are, mathematically speaking, the best way to stay solid in your relationship. That's according to clinical psychologist John Gottman from the University of Washington in Seattle, who has been watching couples bicker about sex and money for more than a decade, gathering data to help him understand the mathematics of matrimony.

New Scientist skriver även om detta i Mathematical formula 'predicts marriage breakdown'.

När jag i somras kollade in differentialekvationer stötte jag på Gottmans "marital interactions" via slashdot-diskussionen med rubriken: The First Steps Towards Asimov's Psychohistory?. Bland annat refererades till Slate-artikeln Love by the Numbers - Can a few differential equations describe the course of a marriage? (från April 16, 2003).

Kursdokumentet Divorce and Marriage gör en differentialekvationsmodellering av giftermål där Gottman nämns. (Några fler exempel på matematisk modellering av sociala fenomen finns via Differentialekvationer - lite mer praktiskt.)


Se även:
John Gottman
Gottmans Love Lab
James D. Murray, som bland annat skrivit Mathematical Biology.
Gottmans och Murrays bok The Mathematics of Marriage: Dynamic Nonlinear Models (från 2003).
The Chronicle: Every Unhappy Family Has Its Own Bilinear Influence Function (April 2003).

Jämför med en annan av Natures Alla hjärtansdag-artikel Unity is the loneliest integer - Internet gives scientists methodologies for dating.

Posted by hakank at 12:26 EM Posted to Matematik

februari 11, 2004

Experimental Mathematics

Niklas Johansson skrev i går om förlegad matematikundervisning i lågstadiet där barnen skulle skriva ned en massa tal i kolumner på ett papper:

Vansinnigt var min spontana tanke... Läroboksförfattarna verkar inte ha följt med i utvecklingen. Talföljder gör man i Excel. Skriv de första talen i några celler och dra ut serien så långt du behöver. Det som tog Joey 10 - 15 minuter att göra, skulle ha tagit högst en minut i Excel.


Detta fick mig att tänka på en bok som jag virtuellt stötte på häromdagen: Mathematics by Experiment: Plausible Reasoning in the 21st Century av Jonathan Borwein och David Bailey (of Pi fame).

Boken, och dess följeslagare Experimentation in Mathematics: Computational Paths to Discovery ("Bok II") av de två ovanstående författarna samt Roland Girgensohn, har en egent sajt Experimental Mathematics Website med mer information. Det finns en "Reader Digest" version av böckerna här (PDF, 72 sidor).

Författarna försöker att få matematiker att acceptera att även "experimentell matematik" och dess resultat är matematik. Boken är full med exempel på sådana bevis (eller är det "bevis"?), t.ex. hur man räknar ut Pi eller arbetar med talsekvenser.

Från förordet (PDF) till bok II:
A typical scenario of using this experimental methodology is the following.
Note in particular the "dialogue" between human and computer, which is very
typical of this approach to mathematical research:
1. Studying a mathematical problem to identify aspects that need to be better understood.
2. Using a computer to explore these aspects, by working out specific examples, generating plots, etc.
3. Noting patterns or other phenomena evident in the computer-based results that relate to the problem under study.
4. Using computer-based tools to identify or "explain" these patterns.
5. Formulating a chain of credible conjectures that, if true, would resolve the question under study.
6. Deciding if the potential result points in the desired direction and is worth a full-fledged attempt at formal proof.
7. Performing additional computer-based experiments to gain greater confidence in the key conjectures.
8. Confirming these conjectures by rigorous proof.
9. Using symbolic computing software to double-check analytical derivations.


Under rubriken Paradigm Shift står:
We acknowledge that the experimental approach to mathematics that we propose will be difficult for some in the field to swallow. Many may still insist that mathematics is all about formal proof, and from their viewpoint, computations have no place in mathematics. But in our view, mathematics is not ultimately about formal proof; it is instead about secure mathematical knowledge.
(Från "Reader Digest"-versionen.)


Målgruppen för böckerna är främst matematiker vilket exkluderar undertecknad, men böckerna verkar ändå intressanta med dess betoning av datorexperiment.


För övrigt finns strängen hakank i Pi, se själv. Länk via David Bailey-siiten ovan.


Uppdatering
Det finns mer information, inklusive Mathematica Notebooks och litteraturreferenser på Matheworld: Experimental Mathematics.

Posted by hakank at 07:48 EM Posted to Matematik | Comments (4)

januari 11, 2004

Mer om 47 och andra (prim)tal

Prime Curios! is an exciting collection of curiosities, wonders and trivia related to prime numbers.. Sajten är en del av The Prime Pages.

Några exempel på Prime Curious (som även täcker sammasatta tal):
47, 52, 99, 77.


Se även Talfördelning på google - varför är det så ont om 52?.

Posted by hakank at 07:16 EM Posted to Matematik

januari 07, 2004

Perfekt kakdelning

Cake-cutting perfected (Nature):

Attempting to share out a cake can easily provoke feelings of injustice. But now a team of mathematicians claims to have found a perfectly fair cake-cutting procedure.
...
Political scientist Steven Brams of New York University and his mathematician and economist colleagues say that apportioning is 'perfect' only if it is efficient, equitable and envy-free. 'Efficient' means that the allocation cannot be made better for any one party while remaining at least as good for all the others. 'Equitable' means that every party values the portion it receives as much as every other party values theirs. And 'envy-free' means that each party thinks it receives the best part, or at least one of several equally good portions.
...
This cake-cutting method can only be made 'perfect' for two or three parties; the researchers have not been able to find such a solution for four. Most disputes over goods or property involve only two or three parties, they point out. Although for cake, they admit, it may be another matter.


Papret som refereras är
Brams, S. J., Jones, M. A. & Klamler, C.: Perfect cake-cutting procedures with money, Preprint, submitted to American Mathematical Monthly (2003).

Se även
Steve Brams
Cake Cutting (MathWorld).

Posted by hakank at 10:25 FM Posted to Matematik | Comments (2)

december 28, 2003

OuLiPo

Det tolfte och trettonde numret av Pequod (se även www.pequod.se) handlar (handlade) om och av den fascinerande litteraturgruppen OuLiPo, som inkluderade författare med namn såsom George Perec, Raymond Roussel, Raymond Queneau, Harry Mathews et cetera etc.

Förutom den lätt (läs svårt) absurda tendensen i skriverierna och dess generativa principer (vilka jag erkänner en definitiv influens av) tycker jag speciellt om de myckna kopplingarna till matematik. T.ex. skrev matematikern Claude Berge en kriminalhistoria där problemet löses med hjälp av grafteori (se Mathematical Fiction: Who Killed the Duke of Densmore? för lite mer info.)

Några av artiklarna i PEQUOD:
Livet är en häst: presentation av gruppen
Teaterträdet - Kombinationskomedi av Paul Fournel (i samarbete med Jean-Pierre Enard).

Några trevliga böcker som innehåller OuLiPo-gruppens alster liksom historik är
Oulipo: A Primer of Potential Literature
Oulipo Compendium (samt www.oulipocompendium.com/)
Oulipo Laboratory: Texts from the Bibliotheque Oulipienne

[Samtliga dessa står inte av en händelse på samma bokhylla bokhyllehylla som mina böcker av Jorge Luis Borges, ordlighetsböckerna, biografin över tidskriften MAD:s grundare Mad World of William M. Gaines samt, men detta är en händelse, ett gäng Kafka-böcker. For easy reference på vägen till köket.]

Mer info:
Oulipo
Mathematics and Literature: Cross Fertilization (PDF)
Harry Mathews
Paul Harris Oulipo-sida

googlesökning på oulipo. Mycket är på franska så 1 fulländade 2 skickliga, talangfulla av och i detta språk har en klar fördel framför oss andra.

Posted by hakank at 08:45 EM Posted to Böcker | Humor | Husgudar | Matematik | Språk | Comments (2)

december 16, 2003

Mathematics could stabilize peace treaties

Mathematics could stabilize peace treaties (Nature):

A political scientist at the Santa Fe Institute in New Mexico has devised a mathematical method that could help civil-war negotiators to find the most stable peace treaties1.
...
Elisabeth Wood calculates that a settlement will be stronger and more likely to last if it finds the ideal way to apportion the stakes. For example, if two warring factions each want control of some part of a disputed region, negotiators need to divide the territory in a way that comes closest to satisfying them both.

Artikeln avslutas:

"I suspect the model is too abstract to be of much practical use," admits Wood, who now intends to test how it might apply to real civil conflicts.

Papret som refereras är Modeling Robust Settlements to Civil War: Indivisible Stakes and Distributional Compromises

Abstract:
Why do some civil war settlements prove robust, while others fail? I show how a settlement’s robustness, defined in terms of the risk factor of the mutual-compromise equilibrium, depends on the nature of the stakes of the conflict and the distributional terms of the settlement. I identify the distributional terms of the optimal settlement, namely, that most robust to exogenous shocks to the actors’ confidence that the other will continue to compromise. I introduce a measure of the degree of the perceived indivisibility of the stakes, an increase in which not only decreases the range of feasible distributional settlements, but decreases their robustness as well. I explore how intra-party heterogeneity and uncertainty regarding ex-post outcomes lessen the range and robustness of settlements. In the conclusion, I compile the predictions of the model and briefly consider the policy implications.

Posted by hakank at 08:16 FM Posted to Matematik

december 14, 2003

Redan de gamla grekerna höll på med kombinatorik

I New York Times-artikeln In Archimedes' Puzzle, a New Eureka Moment berättas om en gammal matematisk gåta (Stomachion) skapad av Arkimedes, som nu fått sin lösning. Eller snarare, man har nu kommit på vilket problem det egentligen var. Det som överraskar historikerna är att man redan på den tiden höll på med kombinatoriska problem.

Twenty-two hundred years ago, the great Greek mathematician Archimedes wrote a treatise called the Stomachion. Unlike his other writings, it soon fell into obscurity. Little of it survived, and no one knew what to make of it.
...
The Stomachion, concludes the historian, Dr. Reviel Netz, was far ahead of its time: a treatise on combinatorics, a field that did not come into its own until the rise of computer science.
...
In fact, he has concluded, the prevailing wisdom was based on a misinterpretation. Archimedes was not trying to piece together strips of paper into different shapes; he was trying to see how many ways the 14 irregular strips could be put together to make a square.

The answer — 17,152 — required a careful and systematic counting of all possibilities. "It was hard," said Dr. Persi Diaconis, a Stanford statistician who worked on it along with a colleague, Dr. Susan Holmes, who is also his wife, and a second husband-and-wife team of combinatorial mathematicians, Dr. Ronald Graham and Dr. Fan Chung from the University of California, San Diego.

Independently, a computer scientist, Dr. William H. Cutler at Chicago Rawhide, a manufacturer of oil seals in Elgin, Ill., wrote a program that confirmed that the mathematicians' answer was correct.
...
The diagram involved 14 pieces, and the word "multitude" seemed to be associated with it. Mr. Heiberg and those who followed him thought this meant that you could get many figures by rearranging the pieces.

"This is part of the reason people didn't see what it was about," Dr. Netz said. But the old interpretation seemed trivial, hardly worth Archimedes' time.

As he examined the manuscript pages, piecing together their text, he realized that what Archimedes was really asking seemed to be, "How many ways can you put the pieces together to make a square?" That question, Dr. Netz said, "has mathematical meaning."

"People assumed there wasn't any combinatorics in antiquity," he went on. "So it didn't trigger the observation when Archimedes says there are many arrangements and he will calculate them. But that's what Archimedes did; his introductions are always to the point."

But did Archimedes solve the problem? "I am sure he solved it or he would not have stated it," Dr. Netz said. "I do not know if he solved it correctly."

As for the name, derived from the Greek word for stomach, mathematicians are uncertain. But Dr. Diaconis has a hunch.

"It comes from `stomach turner,' " he said. "If you get involved with it, that's what happens."


Se även Mathworlds förklaringar:
Stomachion
Combinatorics

Posted by hakank at 08:28 FM Posted to Matematik

december 05, 2003

Mats Anderssons matematiska gåta

För några veckor sedan konstruerade Mats Andersson ett matematisk problem som han beskrev i Århundradets proffsproblem, med kompletterande information och ledtrådar i Århundradets proffsproblem, del 2.

Som Mats senare antydde var det ett problem som jag tyckte var roligt att "sätta tänderna i". Det var en utmaning där det blev lite av en vetenskaplig undersökning. Olika hypoteser ställdes upp: vad händer om man testar detta samband? och funderingar kring "fenomen" gjordes: men hallå, varför är det just på detta viset. Det där kan väl inte vara en slump? ... Det får mig att tänka på.... Eftersom jag är systemutvecklare och inte matematiker skrevs också en del småhack för att testa de olika idéerna. Skoj problem alltså och helt i min smak.

Nu hade jag turen (kombinerad med viss ihärdighet) att till slut komma på rätt lösning. Det blev ett antal rejäla feltänkt några gånger i steg 3, där ett av dessa felskär - en lösning som jag visste var fel, men som löste två av de tre saker jag ställde upp som "fenomen som måste förklaras" - till slut gav mig idén till den slutliga lösningen.

Svaret på gåtas ges i Mats anteckning Århundradets proffsproblem, sista delen!, men försök gärna lösa problemet innan du klickar vidare.



(Johan Asplund jämför i sin "Om undran inför samhället" vetenskaplig forskning med lösning av gåtor och detektivromaner. Det är en underbar liten bok full av intressanta tankar. En summering av boken finns på Johan Asplund - fortolkningens mester.)

Posted by hakank at 12:32 EM Posted to Matematik

november 11, 2003

BBC:s matematikprogram

BBC har en radioserie Antother 5 numbers som handlar om lite olika matematiska ämnen, t.ex. fyrfärgsproblemet och primtal. I programmet The number Seven pratar t.ex. Persi Diaconis om sin teori om kortblandning.

Programmen presenteras av Simon Singh.

Posted by hakank at 08:54 FM Posted to Matematik

oktober 31, 2003

Hängmatematik

Två förslag till svenska ord för "recreational mathematics": hängmatematik
alternativt hängmatte.

Mer om hängmatematik finns i Rekreationell matematik ocn annat tankegodis och Matematikspalter. Se även googles kategori Science > Math > Recreations.

En relativt ny favoritsida är Other Maths av Jon Perry.

Posted by hakank at 08:24 EM Posted to Matematik | Comments (3)

oktober 28, 2003

De svenska myntens talsystem

I Svaret är ungefär 41 - Mynten igen, alltså berättas om en (idealiserad) fördelning av mynten man får tillbaka vid köp.

Här är ett annat sätt att se fördelningen av antalet 10-or, 5-or, 1-kronor samt 50-öringar. Detta sätt utgår från kombinatoriken snarare än simulering.

Man kan se myntens möjliga fördelning som ett eget lustigt talsystem ("de svenska myntens talsystem"), där vi har följande möjliga grundvärden 
  10, 5, 1, 0.5
Jämför med 1, 10, 100, 1000, etc i det decimala talsystemet eller 1, 2, 4, 8, 16 etc i det binära.

I detta mynt-system räknar man lite annorlunda än vanliga talsystem eftersom man här, i en viss (idealiserad) pengar-tillbaka-situation, endast kan få tillbaka ingen (0) eller en (1) 10-krona, 5-kronor respektive 50-öring, medan man kan få tillbaka ingen (0) eller upp till fyra (4) 1-kronor.

Enklast att se detta är att göra en tabell över hur mynten fördelas sig över de 40 möjliga värdena (från 0 till 19.50 i steg om 50-öre).

Kolummnerna är
Pengar-tillbaka-värdet, antal 10-kr, antal 5-kr, antal 1-kr, antal 50-öre 
> cbind((0:39)/2, t(sapply((0:39)/2, function(x) return.change(x))))
      [,1] [,2] [,3] [,4] [,5]
 [1,]  0.0    0    0    0    0
 [2,]  0.5    0    0    0    1
 [3,]  1.0    0    0    1    0
 [4,]  1.5    0    0    1    1
 [5,]  2.0    0    0    2    0
 [6,]  2.5    0    0    2    1
 [7,]  3.0    0    0    3    0
 [8,]  3.5    0    0    3    1
 [9,]  4.0    0    0    4    0
[10,]  4.5    0    0    4    1
[11,]  5.0    0    1    0    0
[12,]  5.5    0    1    0    1
[13,]  6.0    0    1    1    0
[14,]  6.5    0    1    1    1
[15,]  7.0    0    1    2    0
[16,]  7.5    0    1    2    1
[17,]  8.0    0    1    3    0
[18,]  8.5    0    1    3    1
[19,]  9.0    0    1    4    0
[20,]  9.5    0    1    4    1
[21,] 10.0    1    0    0    0
[22,] 10.5    1    0    0    1
[23,] 11.0    1    0    1    0
[24,] 11.5    1    0    1    1
[25,] 12.0    1    0    2    0
[26,] 12.5    1    0    2    1
[27,] 13.0    1    0    3    0
[28,] 13.5    1    0    3    1
[29,] 14.0    1    0    4    0
[30,] 14.5    1    0    4    1
[31,] 15.0    1    1    0    0
[32,] 15.5    1    1    0    1
[33,] 16.0    1    1    1    0
[34,] 16.5    1    1    1    1
[35,] 17.0    1    1    2    0
[36,] 17.5    1    1    2    1
[37,] 18.0    1    1    3    0
[38,] 18.5    1    1    3    1
[39,] 19.0    1    1    4    0
[40,] 19.5    1    1    4    1
En summering av kolumnerna ger: 
> apply(t(sapply((0:39)/2, function(x) return.change(x))),2,sum)
[1] 20 20 80 20
Av de 40 olika möjliga fallen, finns det 20 sätt (20/40 = 1/2) att få tillbaka respektive en 10-krona, en 5-krona samt en 50-öring, men 80 sätt (80/40 = 2) att få tillbaka åtminstone en 1-krona. Här har vi alltså den fördelning som tidigare simulerats fram: 
    c(1/2, 1/2, 2, 1/2)
Om vi normaliserar så att summan blir 1 erhåller man motsvarande sannolikheter att få tillbaka ett speciellt mynt. 
> xx<-c(1/2,1/2,2,1/2)
> xx/sum(xx)
[1] 0.1428571 0.1428571 0.5714286 0.1428571

Antal mynt
Hur många mynt kan vi förvänta oss att få tillbaka? Vi lägger till en sjätte e kolumn med antal mynt som motsvarar en viss summa. Kolumnerna är
Pengar-tillbaka-värdet, antal 10-kr, antal 5-kr, antal 1-kr, antal 50-öre, antal mynt 
> xx<-t(sapply((0:39)/2, function(x) return.change(x)))
> cbind((0:39)/2,xx,apply(xx,1,sum))
      [,1] [,2] [,3] [,4] [,5] [,6]
 [1,]  0.0    0    0    0    0    0
 [2,]  0.5    0    0    0    1    1
 [3,]  1.0    0    0    1    0    1
 [4,]  1.5    0    0    1    1    2
 [5,]  2.0    0    0    2    0    2
 [6,]  2.5    0    0    2    1    3
 [7,]  3.0    0    0    3    0    3
 [8,]  3.5    0    0    3    1    4
 [9,]  4.0    0    0    4    0    4
[10,]  4.5    0    0    4    1    5
[11,]  5.0    0    1    0    0    1
[12,]  5.5    0    1    0    1    2
[13,]  6.0    0    1    1    0    2
[14,]  6.5    0    1    1    1    3
[15,]  7.0    0    1    2    0    3
[16,]  7.5    0    1    2    1    4
[17,]  8.0    0    1    3    0    4
[18,]  8.5    0    1    3    1    5
[19,]  9.0    0    1    4    0    5
[20,]  9.5    0    1    4    1    6
[21,] 10.0    1    0    0    0    1
[22,] 10.5    1    0    0    1    2
[23,] 11.0    1    0    1    0    2
[24,] 11.5    1    0    1    1    3
[25,] 12.0    1    0    2    0    3
[26,] 12.5    1    0    2    1    4
[27,] 13.0    1    0    3    0    4
[28,] 13.5    1    0    3    1    5
[29,] 14.0    1    0    4    0    5
[30,] 14.5    1    0    4    1    6
[31,] 15.0    1    1    0    0    2
[32,] 15.5    1    1    0    1    3
[33,] 16.0    1    1    1    0    3
[34,] 16.5    1    1    1    1    4
[35,] 17.0    1    1    2    0    4
[36,] 17.5    1    1    2    1    5
[37,] 18.0    1    1    3    0    5
[38,] 18.5    1    1    3    1    6
[39,] 19.0    1    1    4    0    6
[40,] 19.5    1    1    4    1    7
Medelvärdet av antal mynt är 
> mean(apply(xx,1,sum))
[1] 3.5
I genomsnitt får vi alltså tillbaka 3.5 mynt tillbaka.

Och så här fördelas frekvensen av antal mynt. 
> table(apply(xx,1,sum))

0 1 2 3 4 5 6 7 
1 4 7 8 8 7 4 1
Dvs det finns 8 möjligheter att få tillbaka 3 mynt, 1 möjlighet att få inga eller 7 mynt osv.


Generaliseringar
Jag kan tyvärr inte garantera att detta var den sista anteckningen om mynts fördelning, eftersom det finns ett antal generaliseringar som kan göras.

Posted by hakank at 01:12 EM Posted to Diverse | Matematik | Comments (3)

Svaret är ungefär 41 - Mynten igen, alltså

Frågan som ger svaret ~41 är lite komplicerad, men den förklaras här nedan.

I Myntfördelningen - en gåta mindre (under Uppdatering) fick vi fram medelvärdet av antal mynt man får tillbaka vid ett köp: I en pengar-tillbaka-situation får man tilbaka, genomsnittligt, 0.5 stycken 10-kronor, 0.5 stycken 5-kronor, 2 stycken 1-kronor samt 0.5 50-öringar. Skrivet i den vanliga fördelningsordningen (10-or, 5-or, 1 kr, 50 öre) 
 (1/2, 1/2, 2,1/2)
Vi vet också att 1 kilo svenska mynt är värda cirka 400 SEK (se Nya rön om mynt-estimering, Håkans viktformel för mynt)

Vi försöker nu få en enkel matematisk formel för att räkna ut totalsumman av värdet samt hur mynten fördelar sig. Problemet kan lösas t..ex. med hjälp av ett symboliskt matematikprogram (obs! här har R inte använts): 
> solve(x*10/2 + x*5/2 + x*1*2 + x*0.5/2 = 400);
                                     41.02564103
Dvs svaret är ungefär 41.

Denna konstant, 41.02564103, använder vi sedan för att räkna ut fördelningen samt totalsumman (som ska bli 400 annars har vi gjort fel).

Per kilo får vi alltså följande antal mynt (något avrundat). 
> 41.02564103 * (1/2,1/2, 2,1/2);  
        (20.513, 20.513, 82.051, 20.513)
Värdet av mynten (något avrundat): 
>  41.02564103 * (10*1/2,5*1/2,1*2,0.5*1/2);
                                (205.123, 102.564, 82.051, 10.256)
Summan av dessa tal blir ~ 400 SEK. Så det stämmer alltså.

Tittar vi på 10 kilo mynt multiplicerar vi helt enkel med 10 och får antalet mynt: 
> 10 * 41.02564103 * (1/2,1/2,2,1/2);
                                (205.128, 205.128, 820.513, 205.128)
Och värdet: 
> 10 * 41.02564103 * (10*1/2,5*1/2,1*2,0.5*1/2);
                                (2051.283,1025.641, 820.513, 102.564)
Kontroll: Summan blir cirka 4000SEK.

Nu fick vi tag i fördelningen: ~ (205, 205, 820, 205)

Vilket ska jämföras med den empiriska fördelningen:
(171, 265, 849, 202)

Exempel
Låt oss nu avsluta med ett fiktivt exempel. Tänk om vi vore i den lyckliga belägenheten att vi har 23 kilo mynt. Hur mycket är detta värt och hur många olika mynt har vi? 

> 23 * 41.02564103 * (10*1/2,5*1/2,1*2,0.5*1/2);              
                 4717.948718, 2358.974359, 1887.179487, 235.8974359
> 4717.948718+2358.974359+1887.179487+235.8974359;
                                     9200.000000
Det är alltså värt 9200 SEK och fördelningen av mynten (antal) är, avrundat till heltal (472, 472, 1887, 472) .

Posted by hakank at 12:54 FM Posted to Diverse | Matematik | Comments (1)

oktober 27, 2003

Nya rön om mynt-estimering

I Hur mycket väger pengar? och Hur mycket väger pengar? - Nu även med lite granularitetsforskning diskuterades hur mycket 10 kilo svenska mynt är värda. Det efterfrågades någon form av approximeringsmetod för att avgöra sådana problem.

Den formel som främst användes (den s.k. Marcus volymformel ) innebär följande approximation:

1 liter SEK-mynt = 1850 SEK

Notera att det är myntens volym som mätes.

Eftersom den förevarande undersökningen mätte cirka 2.5 liter mynt gav det ett estimat på cirka 4600 SEK

Resultat
Nu är pengarna räknade. De fördelade sig på följande sätt:

MyntAntalVärde(SEK)
10kr1711710
5kr2651325
1 kr849849
50 öre202101

Summan blir alltså:

1710 + 1325SEK + 849 + 101 = 3985 SEK

Jämfört med Marcus volymformel slår det på 4600 - 3985 = 615 SEK, vilket trots allt kan anses som relativt bra.

Marcus-Håkan volymformel
Det känns dock tvunget att justera för den uppkomna avvikelsen. Här lanseras alltså den nya Marcus-Håkan volymformel för mynt som innebär en avvägning av de två uppkomna mätvärdena, dvs

1 liter SEK mynt =
(Marcus-värdet + Håkan-värdet)/2 =
(1850SEK + 1594SEK) / 2 =
1722SEK

Vilket sedan avrundas till 1720SEK.

Den nya Marcus-Håkan volymformel för approximering av svenska mynt från volym, är sålunda:
1 liter SEK-mynt = 1720 SEK

Håkans viktformeln för svenska mynt
Här lanseras även Håkans viktformel för svenska mynt (via 10 kg mynt = 3985 SEK ~ 4000 SEK):

1 kg mynt = 400 SEK

Myntens fördelning
Man kan även fundera på varför det är så många 1 kronor (849 stycken) jämfört med övriga mynt (cirka 200 stycken vardera).

Tid och resurser medger för närvarande inte en fullständig analys av detta fenomen. Det kan dock med viss (möjligen stor) sannolikhet antas att fördelningen beror på värden av de existerande sedlarna som även returneras tillsammans med mynten vid en köpprocedur.

Speciellt 20-kronorssedeln måste anses vara viktig för den uppkomna mynt-fördelningen. Detta eftersom just 20 SEK är det minsta värdet för svenska sedlar, vilket är gränsvärdet för penga-tillbaka-returer som kan hanteras i sedlar. Resterande pengar-tillbaka-värden måste alltså returneras i mynt (vilket för oss till den uppkomna myntfördelningen).

Studiet av myntfördelning måste alltså anses vara ett senare forskningsprojekt.

Posted by hakank at 11:13 FM Posted to Diverse | Matematik

oktober 09, 2003

Hur mycket väger pengar? - Nu även med lite granularitetsforskning

I min förra anteckning Hur mycket väger pengar? frågade jag om värdet på 10 kilo ihopsamlande svenska mynt. Efter några intressanta och inspirerande kommentarer försöker jag här konkretisera mina egna tankar. Tack Marcus och Bengt!

Mätande av SEK-mynt i liter
Marcus skrev 2 liter SEK-mynt motsvarar 3700 SEK.

Jag mätte mina mynt till cirka 2.5 liter, så det blir cirka SEK 4600 enligt formeln:

1 liter SEK-mynt = 1850 SEK

Så det besvarar kanske min fråga, dvs 10 kilo SEK-mynt är värda cirka 4600 SEK.

Bengt skrev två saker:
Det första var att 15 kilo (SEK?) blev 2.200 €. Han gjorde sedan ett antagande att 1 liter SEK-mynt = 1 kilo SEK-mynt.
Dock verkar det som om hans antagande

1 liter SEK-mynt = 1 kilo SEK-mynt

behövas justeras lite. Mätt via en vanlig kroppsvåg vägde mina mynt till 10 kilo SEK-mynt. Dvs omvandlingsformeln blir snarare

2.5 liter SEK-mynt = 10 kilo SEK-mynt
dvs
1 liter SEK-mynt = 4 kilo SEK-mynt


Granularitetsforskning
Ett problem att räkna ut via litermått är att det troligen även beror på hur mynten har samlats, skakas eller blandats i den uppsamlande behållaren, vilket i sig kanske beror på fördelning, hur ofta man lägger i mynten etc.
(Mått via kilo är mer konstant vad gäller sådant.)

Vilket får mig att tänka på den "granularitets"-forskningen som jag läste lite om i Nature idag: Think outside the sandbox, skriven av Marc Buchanan, som handlar om forskning kring sands beteende.
One grain of sand is a solid. But a lot of grains together can behave like a solid or a liquid. By probing this dual personality, physicists hope to understand a host of real-world systems, says Mark Buchanan.

Heinrich Jaeger knows what it's like, literally and metaphorically, to watch the sand slipping through the hourglass.
...
A decade ago, Jaeger and his colleagues at the University of Chicago were busy studying what happened when they poured sand into a container and tapped the box repeatedly. They expected the grains to bed down fairly quickly — but, as the team eventually reported in 1995, the sand kept shifting into ever more compact configurations. "Granular systems look deceptively simple," says Jaeger. "But the closer we look, we find so many complexities."

Such puzzles show why granular materials hold a special fascination for physicists interested in the fundamental properties of matter. A pile of sand, flour or mustard seed can stand tall and fixed like a solid, defying the tug of gravity that would bring water sloshing to the floor. Yet sand pours through an hourglass as though it were a liquid.

En annan webbsida om denna forskning är skriven Nathan Bell. Se även program och bilder via projektfilerna (jag har ännu inte fått programmet att kompilera).

Där står det dock inte hur mynt beter sig...


Om "slumpmässig fördelning"
Bengt slog även rask ned på mitt slarviga användande av "slumpmässig fördelning".

Vad jag avsåg var att det inte var någon avsevärd skevhet i mina inköp, såsom att jag skulle använt alla en- och femkronor till parkeringsautomater, eller endast köper kvällstidningen kontant etc.

Snarare menade jag "slumpmässig enligt "växel-tillbaka-fördelningen", som väl i pratform kan beskrivas i stil med "växel fördelat enligt de summor som erhålles efter normala hushållsinköp utan några större avvikelser för en person motsvarande den avsedda demografiska och livsstilmässiga tillhörigheten".

Jag tror alltså det är en speciell fördelning av mynten som, bland annat, beror på följande faktorer:
- vad man köper och hur mycket, dvs mixen av varor. Även vilken typ av hushåll som köper borde vara en påverkande faktor.
- i vilken typ av affär man köper (lågpris, närbutik, specialpriser)
- hur ofta man köper
- hur ofta man betalar med kreditkort
- vilken summa man betalar med (vilket i sig beror på andra saker)
- etc.

Ingen som vill gå vidare med detta och eventuellt få Sveriges Riksbanks pris i ekonomisk vetenskap till Alfred Nobels minne år 2063? :-)

Posted by hakank at 08:48 EM Posted to Diverse | Matematik | Comments (4)

Hur mycket väger pengar?

Jag såg på nuisance value en referens till mycket en viss summa pengar motsvarar.

Det fick mig att tänka på följande: Om man har X (säg 10) kilo svenska mynt, ungefär hur mycket är de värda?

Det (10 kilo) råkar nämligen vara så mycket som jag har lagt undan efter jag fått tillbaka från olika butiker, låt oss säga under ett år. Det är alltså växel från "vanliga köp", dvs hushållsinköp såsom inköp av mat, tidningar etc.

Man kan alltså anta att det är slumpmässigt fördelat - vad det nu innebär här. Den intressanta frågan är just hur de olika mynten fördelas i normal handel under en viss tidsperiod.

Någon som känner till en fin formel för detta?

Posted by hakank at 03:01 EM Posted to Diverse | Matematik | Comments (3)

augusti 17, 2003

Rekreationell matematik ocn annat tankegodis

Mats Andersson var i går på trevligt besök. Jag lovade honom en lista på lite böcker inom ämnet rekreationell matematik (eller är det "rekreativ"?, dvs recreational mathematics), populärmatematik och liknande tankegodis.

Eftersom Mats och jag kommunicerar i princip allting via våra bloggar, så kommer listan här.

Se även min anteckning om Matematikspalter.

Posted by hakank at 11:42 FM Posted to Matematik | Comments (1)

augusti 09, 2003

Matematikspalter

Lite mer om matematik av det lättsammare slaget.

Här är några av mina favoriter bland populärmatematik-kolumner. De handlar alla om intressanta, skojiga eller "useless" fenomen/problem.

De, och några andra, finns även via MAA Online Columns (MAA = Mathematical Association of America), men där finns inte alltid den senaste upplagan.

Posted by hakank at 09:24 FM Posted to Matematik | Comments (1)

augusti 08, 2003

Heltalssekvenser

Mats [inte Kalle som jag skrev först] skriver i sin anteckning Räkna med korthus om ett trevligt litet problem att räkna ut hur många kort man behöver för att bygga ett korthus av en viss storlek.

Jag kommer osökt att tänka på en av mina mest fascinerande böcker: The Encyclopedia of Integer Sequences som består av - förutom ett mycket trevligt introduktionskapitel om hur man beräknar heltalssekvenser - en herrans massa sekvenser av heltal, med små förklaringar och i vissa fall bilder. Den finns även en sajt som innehåller alla sekvenserna i boken, och en massa andra på The On-Line Encyclopedia of Integer Sequences. Besök rekommenderas!

F.ö. har jag boken i två exemplar. Är det någon som vill ha den och kan tänkas komma till Malmö så skänker jag bort det andra exemplaret IRL. Först till kvarn. Skicka ett privat(!) mail till hakank@bonetmail.com. Notera att endast privata mail beaktas. Obs! "Tävlingen" är nu avslutad!

Uppdateringar

1. Boken är nu bortskänkt (i alla fall virtuellt) till Mats Andersson.

2. Jag glömde att nämna att det finns en mailinglista, seqfan, om dessa typer av sekvenser, även om nyheter och förändringar på sajten. Se The SeqFan Mailing List. för mer info.

Det står så här på sidan:
The only requirements to become a member are:

* To have a stable internet mailing address
* To have a keen interest and some creativity about integer sequences

Point 1 is necessary for you to take advantage of a mailing list. Currently for point 2 we require that you contributed at least 5 different sequences to the Online E.I.S.. But this is not that strict, so you can mail me ogerard@ext.jussieu.fr to explain me your interest in seqfan.

Jag har inte skickat in några sekvenser och kommer inte ihåg att jag skrev något mail där jag förklarade mitt intresse. Men det är möjligt de har ändrat det sedan jag började prenumerera, det var ett antal år sedan.

Posted by hakank at 11:50 EM Posted to Matematik | Comments (11)

juli 29, 2003

Problem med slumptalsgeneratorer?

Ytterligare en intressant Natureartikel idag: Random numbers hit and miss om att slumptalsgeneratorer kan vara skeva.

Yet as computers become more powerful, they will be used to carry out bigger simulations - and then the non-randomness will begin to show up. "In times of high precision there is no place for bad random-number generators," says Stephan Mertens of the Abdus Salam International Centre for Theoretical Physics in Trieste, Italy.

Martens and colleague Heiko Bauke of Otto von Guericke University in Magdeburg, Germany, have pinpointed the mathematical cause of this non-randomness. In a supposedly random sequence of 1's and 0's, a typical algorithm tends to cluster zeros together, they show, introducing a bias.

Man bör nog läsa originalartikeln Pseudo Random Coins Show More Heads Than Tails noga.

Abstract: Tossing a coin is the most elementary Monte Carlo experiment. In a computer the coin is replaced by a pseudo random number generator. It can be shown analytically and by exact enumerations that popular random number generators are not capable of imitating a fair coin: pseudo random coins show more heads than tails. This bias explains the empirically observed failure of some random number generators in random walk experiments. It can be traced down to the special role of the value zero in the algebra of finite fields.


Till TODO-listan, alltså.

Posted by hakank at 04:51 EM Posted to Matematik | Comments (5)

juni 22, 2003

Matematisk skönlitteratur

På Mathematical Fiction finns en stor samlig recensioner av skönlitteratur som på något sätt är kopplad till matematik. Dominerande är science fictionromaner/-noveller, men även några pjäser
och filmer finns med.

Posted by hakank at 01:48 EM Posted to Böcker | Matematik

Murphys Lagar och annat

Robert Mathews är en vetenskapsjournalist som har skrivit flera intressanta och tankeväckande artiklar om vetenskap, matematik och sannolikhetsteori. Han har bl.a. undersökt olika Murphys lagar för att se om de verkligen stämmer.

Andra intressanta saker han skrivit:

Se mer på Matthews hemsida och papers- Tyvärr är det många papers som inte finns länkade.

Posted by hakank at 01:25 EM Posted to Matematik