januari 24, 2010
Eureqa: equation discovery med genetisk programmering
(For English readers: This blog post is available as a Google Translation from this Swedish text: Eureqa: equations discovery with genetic programming.)
För mer än 6 år sedan bloggade jag om equation discovery (att hitta ekvationer/samband givet en datamängd) och hittade några roliga system som jag då kollade in rätt mycket.
Nu är det dags igen: Eureqa är ett modernt equations discovery-system baserat på genetisk programming (närmare bestämt symbolisk regression) och det har ett fint GUI etc.
Eureqa blev världskänt i början av december förra året genom att Wired skrev en artikel om systemet och forskningen/forskarna bakom: Download Your Own Robot Scientist. Faktum är att jag laddade ner systemet och testade det lite men jag höll på på med andra saker.
De senaste dagarna har jag suttit med några enkla problem (dvs datafiler) för att lära känna Eureqa mer. Mer avancerade saker såsom dynamiska modeller (differentialekvationer) och komplexa ekonomiska system (såsom börskurser) tar jag tag i senare.
Jag tänker inte gå in på vad genetisk programmering är mer än att säga att det använder inspiration från biologin för att leta rätt på en lösning. Se vidare genetic programming (Wikipedia) för mer info och länkar.
Huvudprincipen för den variant av genetisk programmering som Eureqa använder är att man har
- en datamängd
- ett visst antal matematiska funktioner ("byggklossar")
- en relation mellan variabler som man vill studera
Eureqa hittar då givet variablerna och funktioner ett antal samband (lösningar, modeller). Med en "felfunktion" (error function) kommer diskrepansen mellan data och den skapade modellen att minska till ett så litet värde som möjligt, förhoppningsvis 0.
Här följer några kommentarer och ett och annat tips. Först beskrivs Eureqa, sedan lite mer om modelleringen med några exempel. Efter det länkar till några av de datafiler som används, och sist mer länkar om Eureqa.
Mycket kortfattat: Jag tycker Eureqa är ett riktigt trevlig och skoj system, tyvärr rätt mycket CPU-slukande för att min dator ska må riktigt bra. Men skoj.
Min vana trogen skapades även en My Eureqa page för länkar, filer och annat etc.
Installation
Programmet finns att ladda ner här.Tyvärr finns endast en Windows-version men det ska komma klienter för åtminstone Linux. Jag har inga större svårigheter att köra Eureqa under Wine förutom att det alltså tar väldigt mycket kräm när det bearbetar data.
Det installerades på min burk med följande kommando:
wine msiexec /i eureqa_full_0.7.7.msi
och kör det sedan med
wine "<installation path in Wine>/Eureqa.exe"
Mer om systemet
Eureqa har ett mycket trevligt GUI med olika tabbar för data, plottning/smoothing av data, modellering, start/stop och lösning. Dessa tabbar presenteras här kortfattat.* "Enter Data"
Man kan skriva in data som i ett enkelt spreadsheet à la Open Office Calc eller Excel (vad jag vet stöds inte formler etc). Det sätt jag använder är dock att skapa en text fil (ASCII) som består av följande:
- header med information om fälten. T.ex.
% | x y z |
där "%" är kommentar och de två "|" är avgränsare för variabelnamnen. Tänk på att det bör vara relativt korta namn annars kan det bli svårläst med mer komplexa uttryck.
- sedan data med mellanslag som separator.
För att hämta in en datafil används "File", "Import data...". Om det är fel i filen kommer mer eller mindre lättförståeliga felmeddelanden. Jag har inte testat så mycket att manuellt lägga in data via kalkylprogram men det ska gå.
* "Preview Data" (och smoothing)
I detta fönster man man se de olika värdena plottade i en x/y-graf. Man kan även göra en smoothing (vad jag förstår är det loess man använder), t.ex. om det är mycket brus för någon variabel.
* "Pick Modeling Task"
Här gör man själva modellen, dvs skapar förutsättningen för uttrycket. Se även nedan under "Modellering, några exempel".
- Search for a formula: Här skriver man formen för uttrycket, t.ex.
x1 = f(x2,x3).
- Using building blocks: Här väljs de funktioner ("byggklossar" som man vill att Eureqa ska testa. Normal vill man alltid ha "+","-","*","/", men sedan beror det lite på vad det är för typ av data. Intressant nog är "sin" och "cos" alltid med, vilket väl speglar utvecklarnas preferens för fysiska system. Eftersom de flesta av mina datamändger inte är fysiska system brukar jag börja med att ta bort sin och cos och i stället välja t.ex. square root, exponential och logarithm, eller helt enkelt endast börja med de fyra räknesätten.
Det finns ett flertal andra byggstenar, t.ex. minimum, maximum, Logistic, Gaussian, Gamma, Step och Sign, man inverser och hyperboliska varianter av trigonometriska funktionerna. På forumet antyds att det kommer flera i nästa version, t.ex. de booleanska AND, OR, XOR, samt att man ska kunna definiera egna varianter.
Det finns även andra saker på denna sida, t.ex. att välja Fitness metric och viktningen av datapunkterna.
Det går också att använda flera datorer till en körning. I "Use the following servers" väljer man eventuellt andra datorer som kör en Eureqa server. Detta har jag inte testat.
"Seed previous solution(s)": Här kan man skriva uttryck (formler) som en vink ("bias" till Eureqa att dessa är viktiga formler. Detta har jag inte kollat in så mycket.
* "Start/stop"
Här startar, stoppar och pausar man en körning. Förutom dessa knappar finns en mängd annan information om hur körningen går.
* "Solution Results"
Det är här man ser lösningen både som ett uttryck och även en graf hur bra lösningen är jämfört med de givna datapunkterna. Det är fascinerande att se den växa fram och lära sig.
Datamängden delas upp (automatiskt av Eureqa) innan körningen i två delar: träningsdata (train data) och valideringsdata (validation data). Sedan körs modellen på träningsdatan och valideras på valideringsdatan. Dessa två delar presenteras med olika färger här så man ser hur bra eller dåligt den valda modellen (uttrycket) passar. Mycket trevligt.
Olika statistiska metriker visas för respektive träning- och valideringdata:
- Fitness
- R-squared
- Correlation Coeff
- Mean Squared Error
- Mean Absolute Error
- Minimum Error
- Maximum Error
De flesta av dessa kan man använda som fitness metric i modelleringstabben.
I listan över lösningar ser man en handful lösningar som anses som mest intressanta, med den mest lovande överst. Denna lista växer dynamiskt hela tiden efter hand Eureqa hittar nya modeller. Om man klickar på en av modellerna visar både statistik och plottningen för den valda modellen. Dubbelklickar man på en formel kopieras den för att sedan klistras in i något finns program (t.ex. om man vill blogga om det).
Modellering, några exempel
Här en kort beskrivning om modelleringen. Till skillnad från traditionell "curve-fitting" så skriver man inte några matematiska uttyck som ska parametriseras, utan endast vilka variabler som ska vara med i uttrycket. För dessa variabler väljs om de överhuvudtaget ska vara med samt eventuell parameter. Eureqa hittar även olika konstanter, både "globala" och inom uttryck.Exempel med sinus
En av de första sakerna jag testade var att skapa en datafil med två kolumner (x och y) skapad på följande sätt (med Perl):
perl -le 'for (-100..100) { print $_/100, " ", sin(2*$_/100)+3}'
som skapar data för sambandet y = sin(2*x) + 3. De sparades i datafilen sin_formula.txt.
Eureqa hittar lösningen efter cirka 10-15 sekunder. Notera att x motsvaras av "x0" och y av f(x0) (eller x1):
f(x0) = 3 + sin(2 * x0)
Detta var alltså 201 datapunkter, men man behöver inte alls så mycket data för att Eureqa ska hitta en lösning.
En variant där man endast tar 20 slumpmässiga punkter är sin_formula_rand20.txt som är skapad genom att ta 20 punkter mellan 0 och 2*Pi:
perl -le 'for (1..20) { my $x = rand(2*3.14159); print "$x ", sin(2*$x)+3}'
Eureqa hittar 3+sin(2*x0) på cirka 30 sekunder. Det gick (denna gången i alla fall) lite långsammare eftersom det är färre punkter. Man ska dock komma ihåg att färre punkter gör att det är snabbare att kontrollera hur bra lösningen är.
Den viktigaste delen i modelleringen, förutom att hitta tillförlitlig data, är att hitta rätt byggstenar, dvs de matematiska funktioner som ska användas. Det bör göras med viss försiktighet och eftertanke: Om man väljer för många kan det ta väldigt lång tid och man kan får konstiga resultat. Väljer man för få så hittas inte en enkel lösning. Detta är en konst.
Fibonacci-serien
En annan skoj sak som man kan testa är tidsserier eller data som kan ses som tidsserier. T.ex. kan Eureqa hitta en formel för Fibonacci-serien? De 25 första talen i Fibonacciserien är: 1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181,6765,10946.
För att göra detta till en lämplig representation - och som vanligt är representationen av problemet väldigt viktigt - är att man tar (tids)serien och lägger den i sekvens över flera variabler.
Låt oss anta att vi inte vet så mycket om denna serie, men anar att det finns en rekursivitet i serien, dvs att senare värden beror på de tidigare, normalt de omedelbart föregående (andra tidsserier, till exempel de ekonomiska kan ha andra beoenden såsom säsonger och veckodagsberoenden).
Här tas serien om fyra. Den första raden är 1,1,2,3, och sedan förskjuts serien för varje rad. Hela serien finns alltså i första kolumnen.
% | t1 t2 t3 t4 |
1 1 2 3
1 2 3 5
2 3 5 8
3 5 8 13
5 8 13 21
8 13 21 34
13 21 34 55
21 34 55 89
34 55 89 144
55 89 144 233
89 144 233 377
144 233 377 610
233 377 610 987
377 610 987 1597
610 987 1597 2584
987 1597 2584 4181
1597 2584 4181 6765
2584 4181 6765 10946
4181 6765 10946 17711
6765 10946 17711 28657
10946 17711 28657 46368
Nu kan vi modellera problemet i Eureqa på följande sätt:
- Formel: t4 = f(t1,t2,t3)
- Byggklossar: "+","-","*","/"
Det tar mellan 5 och 10 sekunder för Eureqa att hitta sambandet:
t4 = t3 + t2
Correlation Coefficient är 1.00000, R-squared är 1 och alla error är exakt 0 så det ser helt korrekt ut.
Detta är skoj!
Man kan här notera att egentligen behövde vi ju bara de tre första variablerna t1, t2 och t3 men jag valde att ta med den extra kolumnen t4 för att inte fuska för mycket. En annan sak att notera att det är viktigt att titta på Correlation Coefficient och R-squared samt Error för att se hur bra lösningen är.
Nu kan man göra lite mer roliga saker. Given en lite större datamängd (fib_38.txt) med 38 värden kan vi kolla om Eureqa hittar några andra samband, t.ex. mellan endast två variabler t1 och t2, dvs mellan ett värde och endast de närmast föregående. Här lägger jag till funktionerna "exp", "sqrt" och "log".
Här är några samband som hittades i flera olika körningar. Samtliga dessa har en fitness error på 0.000 (det som i lösningstabben kallas "Error") och correlation coefficient på 1.0
f(t1) = 1.61803*t1
f(t1) = 1.61803*t1 - 0.472137/t1
f(t1) = 1.61803*t1 - 1.67999/exp(t1)
f(t1) = 1.61803*t1 - 1.67999/exp(t1)
f(t1) = 0.809017*t1 + 0.809017*sqrt(t1)*sqrt(t1) - 0.470881/t1
f(t1) = 1.61803*t1 + 0.221196/(t1*t1 - 1.61571*t1 - 1.70552)
f(t1) = 1.61803*t1 + -3.39888*log(t1)/exp(t1*t1 - 1.69947)
f(t1) = (1.61803*t1*t1 - 0.459213)/t1
f(t1) = 1.61803*t1 - 0.440428/(t1 - 0.440428/(1.61803*t1))
f(t1) = 1.61803*t1 - 0.3884/(t1 - 0.354305)
Notera att Eureqa har identifierat konstanten 1.61803 i flera av ovanstående lösningar vilket är väldigt nära phi, dvs "gyllene snittet" (golden ratio) = (1+sqrt(5))/2 ~ 1.6180339...). phi är precis förhållandet mellan två intilliggande Fibonaccital, så det är ju inte konstigt att Eureqa hittade detta samband. Se Fibonacci number på Wikipedia och Encyclopedia of Integer Sequences:A000045 för mycket mer info om detta.
Man kan säkert hitta andra matematiska konstanter om man letar vidare. Plouffe's Inverter är en guldgruva för sådant. T.ex. här är en sökning på konstanten 1.61803. Tyvärr är det väldigt många träffar eftersom det är så liten precision på talet.
Formeln f(t1) = 1.61803*t1 är alltså en approximering av nästa tal i Fibonacci-serien, dvs F[n+1] = phi*F[n] (avrundat till heltal).
Ett mera avancerat exempel är om Eureqa månne kan hitta den slutna formeln för Fibonaccital, dvs
F(n) = (phi^n - (1-phi)^n)/sqrt(5)
För detta krävs en ytterligare parameter i datafilen, nämligen n, dvs index för raden. Så här ser filen ut nu (fib_50.txt"), utökat till 50 rader. Den första kolumnen är alltså index.
% | ix t1 t2 t3 t4 |
1 1 1 2 3
2 1 2 3 5
3 2 3 5 8
4 3 5 8 13
...
48 4807526976 7778742049 12586269025 20365011074
49 7778742049 12586269025 20365011074 32951280099
50 12586269025 20365011074 32951280099 53316291173
Jag vet inte riktigt hur stora tal som Eureqa kan använda, men det saknas i alla fall stöd för arbiträr precison.
När jag skapat filen testades först med samtliga variabler:
t4 = f(ix,t1,t2,t3)
Då kommer lite mer avancerade förslag än tidigare körning, samtliga med Error 0 och correlation coeff på 1.0000 (dock inte med Maximum error 0), några av dem innehåller n, dvs index.
f(ix, t1, t2, t3) = sqrt(1.61803*t2*t3) + (t2*sqrt(t3) - t2*t2)/(sqrt(t3) - t2)
OK, nu till problemet om den slutna formeln
Formel: t1 = f(ix)
Funktioner: +,-,*,/, sqrt
Det vi vill ha är alltså något som liknar:
(phi^n - (1-phi)^n)/sqrt(5)
eller snarare den numeriska motsvarigheten
f(ix) = (1.61803^ix - (1-1.61803)^n)/2.2361
= (1.61803^ix - (-0.61803)^n)/2.2361
= 0.4472071911*1.61803^ix - 0.4472071911*(-0.61803)^ix
(Den tredje varianten hittades via ett matematikverktyg.)
Intressant nog började Eureqa med lösningar där endast ix upphöjt till stora tal (t.ex. 18) samt addition, multiplikation med konstanter. Efter ett tag började experimenten med sqrt, men den körningen hittade inte skoj på många minuter så jag stoppade den.
För att komma runt detta testade jag "hints", dvs "Seed previous solution(s)" på "Pick Modeling Task"-tabben, genom att skriva 1.61803^ix samt sqrt(5). Då kom följande lösningar efter liten stund. De har alla korrelationskoefficient på 1, Error på 0 men stora Maximum Error.
f(ix) = ix + 4*ix*ix*ix + 0.0256922*ix*1.58422^ix
f(ix) = 0.445386*ix + 0.445386*1.61817^ix
f(ix) = 0.0893707 + 0.399785*sqrt(1.61804^ix) + 0.447094*sqrt(1.61804^ix)*sqrt(1.61804^ix)
f(ix) = 2*ix + 0.447097*1.61804^ix
f(ix) = 0.611078*sqrt(1.62499^ix) + 0.447094*1.61804^ix - 127.933
Jag undrar dock hur "naturligt" det är för Eureqa att testa formler på formatet "konstant^variabel", så detta anser jag vara lite fusk. Däremot, om det skulle gärna mer seriösa experiment är denna typ av hintar vettiga. Då anger man vissa samband som grund, ett "alfabet" att bygga vidare på. Jag tror att mer stöd för detta kommer i senare versioner.
Efter detta - ska vi säga misslyckande - skippade jag hintarna och lade på funktionerna "exp", "sin", "cos" och då hittades detta samband och flera liknande, som jag faktiskt inte vet hur det ska tydas. Vad är 0.481188 för något tal i detta sammanhang?
f(ix) = 0.447755*exp(0.481188*ix) - 0.481188*ix*ix*ix
Om man däremot lägger till funktioner "power" (och tar bort alla hintar) så kommer lösningar på formen konstant^ix väldigt snabbt (dvs inom en minut eller så), t.ex.
f(ix) = 32.1653 + 0.446572*1.61809^ix
Där vi möjligen kan ana phi i konstanten 1.61809.
En kommentar om "power": När man väljer den i funktionslistan kommer meddelandet Tip: integer powers are implemented automatically with the multiply operation. This more general power operator may not be needed for modeling the dataset.. Här har vi tydligen ett fall där "power" behövs.
Andra lösningar i olika körningar:
f(ix) = 1.61808^(ix - 1.67492)
f(ix) = 0.0893756 + 0.399799*1.27202^ix + 0.447099*1.27202^ix*1.27202^ix
f(ix) = 1.61804^(ix - 1.67287) + 1.61804^(0.478442*ix - 0.800371)
f(ix) = 1.26564^(2*ix - 1.26564) + 2*ix - 1.26564
f(ix) = ix + 0.447144*1.61804^ix
(Jag har inte analyserat vidare eventuella matematiska samband...)
Notera att även om det är 0 i Error och 1 i korrelationskoeffient så kan det vara stora fel när man pumpar i konkreta värden.
En intressant lösning är följande där man möjligen kan skymta de viktiga beståndsdelarna i den slutna formeln:
- sqrt(5) ~ 2.2361
- 0.4472071911*1.61803 (från tredje varianten av den sökta formeln)
f(ix) = 2.23642*ix + 0.447144*1.61804^ix
Mer komplexa varianter:
f(ix) = 0.447144*1.61804^ix + 2.61804*ix*ix - (ix*ix)^(ix - 48.6408) - 48.6408*ix
Efter detta avslutade jag testet p.g.a. tidsfaktorer.
Slutsats: Vi hittade alltså inte formeln under dessa experiment, men vissa av sambanden kanske kan vara intressanta att studera vidare. Och så lärde vi oss det där med "power". En annan sak detta visar är att man kan vara tvungen att starta om flera gånger för att få mer aptitliga lösningar.
Derivata
Som nämnts några gånger tidigare så har jag inte labbat så mycket med dynamiska modeller, ävenom Eureqa skapats för detta ändamål. En av anledningarna är att jag inte har så bra data tillgänglig, en annan är att de mer intressanta körningarna kan ta lång tid, i vissa fall många timmar; "över natten" är ett uttryck som används några gånger i skrifterna.
Som videon (se Eureqas hemsida för länk) visar finns det möjlighet att använda derivata på följande format:
D(x1,t) = f(x1,x2,t)
och även i högerledet
D(x1,t) = f(x1,x2,D(x2,t))
Andra derivatan skrivs på följande sätt:
D(x1,t,2) = f(x1,x2,t)
Man ska dock tänka på att med derivata så krävs en preprocessing som kan ta mycket lång tid.
Andra modelleingsexempel beskrivs nedan.
Datafiler
Här är några av de datafiler som jag testat. För det mest är det enklare saker, och inte någon dynamisk data. De läses in med "File", "Import data...". Datafilerna finns även att tillgå på My Eureqa page.- gelman.csv: Linjär regressionsexempel.
Data från Andrew Gelman's bloggpost Equation search, part 1, Equation search, part 2. Problemet beskrivs även lite mer i A linear regression example, and a question.
Skriv följande i Pick Modelling Task:
y = f(x1,x2)
och lägg till "sqrt" som funktion.En lösning är mycket riktigt
f(x1,x2) = sqrt(x1^2+x2^2)
Med en korrelationskoefficient på 1.0 (och det är alltså bra). - planets.txt: Keplers tredje lag
Detta exempel baseras på DTREG, ett annat symboliskt regressions-verktyg. Här hittas Keplers tredje lag baserat på den data som Kepler hade. Keplers tredje lag är:
Period^2 = Distance^3
Formel:
Period = f(Distance)
Funktioner: Skippa sin och cos, lägg till square root, exp och logarithm.Eureqa hittar rätt snabbt samband såsom:
Period = sqrt(Distance)*Distance
och det går snabbt. - odd_parity.txt
En test på "paritet", men det funkar inte eftersom Eureqa än så länge saknar booleanska operatorer såsom OR, AND och XOR. Det ska komma "snart". - sin_formula.txt
Se ovan. - sin_formula2.txt
Se ovan. - sqrt_formula.txt
Skapad så här:
perl -le 'for (-100..100) { print $_/100, " ", sqrt(abs(2*$_/100))+3}'
Glöm inte att lägga till sqrt, abs och lite andra funktioner. - iris.txt: Iris data
Iris är ett standardproblem (-datamängd) inom machine learning och traditionell multivariat statistisk analys. Se Iris flower data set (Wikipedia) för mer information. Kortfattat handlar det om att klassifiera tre olika blomtyper (Iris setosa, Iris virginica and Iris versicolor) med avseende på fyra attribut: (Sepal Length, Sepal Width, Petal Length, Petal Width). 50 mätningar gjordes för respektive blomtyp.Jag tänkte att det skulle vara skoj att testa det med Eureqa också. Tyvärr klarar inte Eureqa att hantera kategorier (dvs strängrepresentation) så jag döpte om dem till "1", "2", samt "3" vilket troligen förvirrar Eureqa. En standardlösning för visssa typer av analysverktyg/-metoder som inte klarar kategorier är att i stället använda tre binära variabler som representation för de tre kategorierna. Men jag vet inte hur man får in sådant i Eureqa.
Jag började med att representera attributen som
sepallength, sepalwidth, petallength, petalwidthmen det blev så trångt i lösningsfönstret att jag ändrade till kortnamnensl, sw, pl, pw.Problemet skrivs på följande sätt
class = f(sl, sw, pl, pw)
Första körningen, med standarduppsättningen "+","-","*","/" samt "sin" och "cos" gick inte alls bra. Men när - som experiment - jag lade till funktionerna "minimum", "maximum" och "sqrt" så hittas följande rätt snart
class = f(sl,sw,pl,pw) = max(1,pw + 2.20/sw)
med en error på 0.179, fitness på -0.18, correlation coeff på 0.96, mean squared error 0.04. Traditionella metoder inom data mining/machine learning såsom beslutsträd brukar ligga ungefär där med 5-10 felklassificerade instanser.Efter lite mer tuggande kommer några bättre lösningar.
error 0.129:
f(sl, sw, pl, pw) = 0.975279 + min(0.624122*pw*pw, 2.02407)
error 0.124:
f(sl, sw, pl, pw) = 0.926007 + min(max(0.63846*pw*pw, 0.0735181), 2.07556) Jag är inte nöjd med detta eftersom min och max inte är så naturliga i sammanhanget och jag har inte analyserat vidare ramifikationerna av detta. Men det är ett roligt experiment. Man skulle kunna gå vidare och kontrollera vad som händer om man representerar de tre kategorierna med talen 100, 200, 300 istället, eller lägger till andra funktioner såsom sign etc.
Som jämförelse kan nämnas att andra metoder (t.ex. via machine learningverktyget Weka) ger följande resultat, båda med ett antal felklassifikationer.
J48 (beslutsträd):
petalwidth <= 0.6: Iris-setosa (50.0)
petalwidth > 0.6
| petalwidth <= 1.7
| | petallength <= 4.9: Iris-versicolor (48.0/1.0)
| | petallength > 4.9
| | | petalwidth <= 1.5: Iris-virginica (3.0)
| | | petalwidth > 1.5: Iris-versicolor (3.0/1.0)
| petalwidth > 1.7: Iris-virginica (46.0/1.0)
JRIP (regelbaserad method):
(petallength <= 1.9) => class=Iris-setosa (50.0/0.0)
(petalwidth >= 1.7) => class=Iris-virginica (48.0/2.0)
(petallength >= 5) => class=Iris-virginica (5.0/1.0)
=> class=Iris-versicolor (47.0/0.0)
Se även min My Weka page för mer saker om Weka.
- Sunspots.txt: Sunspots
Solfläcksdata är ett annat standardproblem inom statistik och tidserieanalys. Tyvärr är jag lite osäker på vad denna data kommer ifrån, men det ska mätning av solfläckar på årsbasis. Så ta följande med en viss nypa salt och se det som ett generellt experiment.Detta är alltså en tidsserie med 11 "förskjutna" variabler.
Formel
t11 = f(t1,t2,t3,t4,t5,t6,t7,t8,t9,t10)
Funktioner: +,-,*,/, sin, cosNotera att jag lät sin och cos vara med men de användes inte under den cirka halvtimmen jag körde (förutom några tidigare lösningar som förkastades snabbt).
Efter ett par minuter var följande med i listan över aktuella lösningar (avrundat till 2 decimaler):
Error: Solution
0.215: 0.65*t10 + 0.66* (t10 / (0.32+0.08*t8)
0.237: 7.20+1.34*t10 - 0.58*t9
0.261: 1.39*10-0.54*t9
0.302: 1.91*t10-t9
0.307: t10-0.19*t9
0.342: 0.84*t10
0.400: t10
Ingen av lösningarna är speciellt bra. Vi ser dock att t10 - inte förvånande - alltid är med, ibland t9 och vid ett tillfälle (det bästa) med t8 vilket visar att det finns någon form av beroende av tidigare värden.
- sin_formula_rand20.txt
Skapad med följande:
perl -le 'for (1..20) { my $x = rand(2*3.14159); print "$x ", sin($x)+exp($x)+3}'
Hittar följande snabbt:
3 + exp(x0) + sin(x0)
Testar genom att skippa sin(), men låter cos() vara kvar. Det tar en stund, sedan hittar den följande
3.00 + exp(x0) + cos(1.57-x0)
- boyles_law.txt: Boyles gaslag
Se mer på Wikipedia Boyle's law.Detta är en klassiker i sammanhanget (dvs equation/scientific discovery), från boken Langley et.all Scientific discovery (ISBN: 9780262620529, länk till Bokus), sidan 82. Boken beskriver hur systemet BACON angriper problemet. BACON är ett system med liknande intentioner som Eureqa men använder en annan teknik. Boken är för övrigt mycket intressant.
Eureqa hittar relativt snabbt samtliga samband (vid var sin körning):
PV = P*V
V = PV/P
P = PV/V
Corelation coeff är 1 och mean error i princip 0.Intressant nog kommer under körningen
VP=f(V,P)även andra samband efter en stund:
f(V, P) = (V*P*cos(-1*P - 1.36791) - V*P*P)/(cos(-1*P - 1.36791) - P)
- fib_25.txt: Fibonacci
Se ovan.
- fib_35.txt
Se ovan. - catalan.txt: Catalan-talen.
Har inte hittat något skoj hittills, men ska nog leta vidare...
- not_squares.txt
Tal som inte är kvadrater. Hittade inget skoj. - primes.txt: Primtal
Detta är också en tidsserie-variant med 10 variabler för att se om något skoj samband hittas. Även här får man leta vidare. - primes_with_index.txt: Primtal med index (dvs ordningstalet för primtalet)
Se ovan om primes.txt - p4_gap.txt: Polynom
Detta är ett av exempelproblem från JGAP (ett generellt genetisk programmingssystem i Java) där problemet är att hitta polynometx^4 + x^3 + x^2 - x.Detta tog cirka 30 sekunder att hitta denna funktion i Eureqa. Notera att jag tog bort "sin" och "cos".
Som jämförelse kan nämnas att JGAP-versionen tog cirka 12 minuter (vid första och enda körningen), men det är inte en rättvis jämförelse eftersom Eureqa är optimerat för denna typ av körningar. Uppdatering: . Jag noterade att anledningen till att det tog så lång tid i JGAP var att det inte fanns några operatorer för Add (+) eller Subtract (-) vilket ju gör problemet mycket svårare. När dessa lades till (samt Sine och Exp togs bort) tog det cirka 10 sekunderi JGAP. JGAP är helt klart ett intressant system för genetisk programmering.
- p4_1.txt: Polynom
Jag skrev ett litet program som skapar slumpdata för polynom på formenx^n+n^(n-1)+...n^2+x^1+x. Sådan problem kallar jag förp(n)nedan.Detta är alltså
p(4). Det tog Eureqa cirka 20 sekunder att hitta
p(4) = x^4 + x^3 + x^2 + x
baserat på 30 punkter x,y inom intervallet -5.0..5.0. - p10_1.txt Polynom P(10)
Däremot var det lite problem med p(10) över intervallet -2.5..2.5 och 100 punkter. Jag startade om ett antal gånger efter att ha väntat - ovetenskapligt nog - "några minuter .Rätt tidigt hittades x^10+x^8+x^7 men sedan tog det stopp
och Eureqa började labba med x^12, t.ex.(x^12-x^2)/(x^2-x).En trolig förklaring till detta är att Eureqa straffar flera termer till förmån för färre.
Jag startade om och ändrade Fitness Metric till "Maximum Error" (på tabben "Pick Modeling Task"). Efter cirka 6 minuter hittades
0.73*x+x^2+x^3+x^4+x^5+x^6+x^7+x^9+x^9+x^10
med ett Maximum error på 1.76. Correlations coefficienten är 1.0000 vilket ju är bra.Lösningen
(x^12-x^2)/(x^2-x)
har ett mindre felvärde för den datamängd jag testade, det var ju bara 100 punkter, så en del kan förklaras utifrån slump.Jag tröttnade efter typ 20 minuter.
- p6_1.txt: p(6)
- p7_1.txt: p(7)
- circle_1_fixed.txt: Cirkel
Detta är ett av exemplen till Eureqa, som finns att laddas ner här. Tyvärr är de i ett konstigt format så jag var tvungen att snygga till dem lite, härav namnet "_fixed.txt".
Formel:
x3 = f(x1,x2)Hittar lösningen 4*sin(x1) på 20 sekunder.
Formal:
x2 = f(x1,x3)
Hittar lösningen 4*sin(x1) på 20 sekunder.Testar nu derivata:
Formel:
D(x3,x1) = f(x1,x2)
Lösningen verkar vara
dx3/dx1 = x2
Testar formeln
D(x3,x2) = f(x1,x2)
Lösningen är 0 som Eureqa hittar omedelbart.Formeln
D(x2, x1) = f(x1, x3)
ger lösningenx3.
Mer om Eureqa
Här är en samling länkar om Eureqa.- Download page
- User Guide (PDF)
- Discussion Group (google group)
- FAQ
- Video: "Introduction to Eurequa" finns via Eureqa-sidan, och även på Youtube: Introduction to Eureqa (1/2) samt Introduction to Eureqa (1/2)
- Hod Lipon och Michael Schmidt är utvecklarna av Eureqa. Deras Science-artikel Distilling Free-Form Natural Laws from Experimental Data, supplemental materials (PDF). Mer finns på Sciences sajt Distilling Free-Form Natural Laws from Experimental Data, Supporting Online Material, med bl.a. den data som används invar_datasets.zip. Som nämndes ovan är datafilerna konstiga (i alla fall i min miljö) och måste fixas till.
Mer om symbolisk regression som är den metod Eureqa använder: Symbolic regression (Wikipedia)
* Andra artiklar om Eureqa:
- Wired: Download Your Own Robot Scientist
- Guardian: 'Eureka machine' puts scientists in the shade by working out laws of nature
- Physorg.com: Eureqa, the robot scientist (w/ Video)
- Andrew Gelman (bloggar på "Statistical Modeling, Causal Inference, and Social Science"): Equation search, part 1, Equation search, part 2.
Posted by hakank at 09:16 FM Posted to Dynamiska system | Machine learning/data mining | Pyssel | Statistik/data-analys
juni 06, 2008
Blogglunch söndagen den 15/6 kl 13.00 samt Markovgenererade bloggträffsammanställningar
Zyrenna-Åsa manar till Blogglunch söndagen den 15/6 kl 13.00, naturligtvis på restaurangen Kin Long. Meddelena Åsa om du tänker komma.
Med anledning av en semantisk förrvirrning angående tidens riktning i en första version av kallelesen skriver hon i kommentarsflödet:
Någon borde testa [att skriva refererat för framtiden]. Skriva referatet i förväg och sedan jämföra med utfallet.
Sammanställningar om redan hända bloggträffar har gjorts. Men att skapa sammanfattningarna innan? Detta kändes som en utmaning!
Eftersom jag är alldeles för lat för att fantisera fram diskussionerna på en hel bloggareträff gjordes det näst bästa: utgick från de redan skriva sammanfattningarna. Det blev det Markovgenerering - inte helt förvånande för den som följt med ett tag. Se t.ex. Generering av Nobelpris-motiveringar (Markov såklart) för mer om Markovgenerering av texter.
Det aktuella programmet som skapar bloggträffsammanfattningar är Markovgenererade bloggträffsammanfattningar.
Om texten inte upplevs vara helt korrekt svenska, föreställ då att författaren är smått förvirrad, berusad eller skriver aningen för snabbt . Eller helt enkelt är poetiskt kryptisk, en kryptopoet .
Posted by hakank at 08:43 EM Posted to Bloggmiddagar | Språk | Statistik/data-analys | Comments (1)
oktober 28, 2007
Svar på Hakkes frågor angående monovokala ord
Den alltid nyfikne hakke skickade följande mail till Jonas Söderström och mig häromdagen. (Mailet är trivialt redigerat.)
Det går ju inte att kommentera den här gamla godingen :( Ooo, så långa ordSå jag får mejla kommentaren istället :)
/Håkan (hakke)
Vissa saker man läst sitter liksom kvar i hjärnan som en lös liten
skruv, som ibland vickar till och gör sig påmind. Dit hör det här
inlägget, bland annat för att det var här jag upptäckte bloggarna men
också på grund av dess språkglädje.Nyss stötte jag på ordet "kulturutbud" i en text. Det är inte särskilt
lättläst, en egenskap det troligen delar med många andra monovokala
ord.Håkan Kjellerstrand hade ju vänligheten att publicera följande lilla
lista över förekomsten av monovokala ord för var och en av svenskans
vokaler:
Vokal: antal ord
----------------
a: 3137
e: 791
i: 1299
o: 960
u: 625
y: 192
ä: 590
å: 280
ö: 272
Några saker jag blir nyfiken på är:
Efter kom sedan tre (3) frågor som av besvaras (eller åtminstone bekommenteras) var och en i det nedanstående. Notera att ordlistan som användes för att skapa ovanstående förekomstfördelning är äldre i relation till den ordlista som används i dessa svar.
Hakkefråga 1. Vilka är de längsta fem monovokala orden för varje vokal?
Svar fråga 1.
Här är de inte bara de fem utan även de sex längsta ord för respektive monovokal . Ordlängden visas efter ordet. Not: Det kan finnas flera ord med samma ordlängd som den minst långa ordlängden för respektive vokal. Programmet visar då endast att det blir exakt sex stycken ord (och slumpmässighetens underbara men samtidigt starkt underskattade men starkt påverkande hand styrde exakt vilka som visas).
Vokal a:
brandalarmapparat: 17
andrahandsmarknad: 17
partssammansatt: 15
branschanpassad: 15
brandhandgranat: 15
tandspacklarnas: 15
Vokal e:
referensfrekvens: 16
frekvensmeterns: 15
telexreglemente: 15
referenselement: 15
meddelelsemedel: 15
pendelfrekvens: 14
Vokal i:
lindningsriktning: 17
tillfriskningstid: 17
lindningsstigning: 17
drivningsriktning: 17
visningsspridning: 17
stigningsriktning: 17
Vokal o:
motorfordonskontroll: 20
kontrollprotokoll: 17
domstolsprotokoll: 17
torvjordskompost: 16
fordonskontroll: 15
kontrollmottolk: 15
Vokal u:
ursprungspunkt: 14
djupbrunnspump: 14
sunhultsbrunns: 14
grundstruktur: 13
sunhultsbrunn: 13
kugghjulspump: 13
Vokal y:
skyddshytt: 10
styckfryst: 10
krymptryck: 10
tryckstyrd: 10
plymprydd: 9
frysskydd: 9
Vokal å:
stålspåntlås: 12
språngstråk: 11
tvångsvård: 10
stånggång: 9
nålsprång: 9
ståltråds: 9
Vokal ä:
rättshjälpsnämnd: 16
kärrsnäppsägg: 13
vändskärsfräs: 13
rännhärdsjärn: 13
skräntärnsägg: 13
ändskärsfräs: 12
Vokal ö:
mörkrödglöd: 11
bröstsköld: 10
förströtts: 10
bröstmjölk: 10
slöjdbjörk: 10
bröstböld: 9
Hakkefråga 2. De korta orden intresserar mig inte särskilt mycket. Det skulle vara intressant att se motsvarande sammanställning begränsad till de ord där det finns minst 3, 4 respektive 5 vokaler. Jag gissar att fördelningen mellan ordrikedomen per vokal då också kan komma att förändras något. Kanske blir ledningen för a och i ännu tydligare?
Svar fråga 2
Först kommer den totala fördelningen av antal vokaler per ord som har
minst 2 vokaler för att få en känsla för vad som kommer:
Fördelning av antal vokaler per ord:
2: 9868
3: 3215
4: 539
5: 60
6: 6
Sedan med hakkes föreslagna begränsningar om minst v vokaler.
Vanligaste bokstaven (minst 2 monovokaler):
a: 7377
e: 2080
i: 1612
o: 1275
u: 436
ä: 410
ö: 253
å: 196
y: 49
Vanligaste bokstaven (minst 3 monovokaler):
a: 2447
e: 717
i: 350
o: 229
u: 64
ä: 9
å: 2
ö: 2
Vanligaste bokstaven (minst 4 monovokaler):
a: 354
e: 179
i: 38
o: 33
u: 1
Vanligaste bokstaven (minst 5 monovokaler):
a: 42
e: 16
i: 4
o: 4
Vanligaste bokstaven (minst 6 monovokaler):
e: 4
a: 1
o: 1
Det finns inga ord i ordlistan med 7 eller fler monovokaler.
För fullständighetens skulle visas här även fördelningen av ordlängden (för ord med minst 2 monovokaler):
3: 22
4: 300
5: 1226
6: 2486
7: 2964
8: 2744
9: 1886
10: 995
11: 517
12: 299
13: 151
14: 62
15: 16
16: 6
17: 13
20: 1
Hakkefråga 3. Undrar om fördelningen ändras över tiden? Sedan listan skapades har det ju kommit en ny version av saol.
Svar (eller snarare kommentar till) fråga 3
Hakke har troligen en poäng att ovanstående beskrivna fördelningar förändras över tiden. Det är dock utanför mitt experimenterande eftersom jag inte använder SAOL utan Den stora svenska ordlistan (eller snarare ett derivat av den ordlista man kan ladda ner här och om vilket kommenteras något mer här nedan).
Svar på anticiperad följdfråga: Nej, jag har inte sparat olika DSSO-versioner för denna typ av jämförelse.
Några vidarekommentarer
För ett antal (cirka 2) månader sedan förnyades monovokaldiskussionen på Blind Höna, i Ooo, så många o:n! Monovokal toppnotering tangerad (där mina findings bygger på samma ordlista som ovanstående analyser). Se även Söndagspyssel där den ursprungliga monovokaldiskussionen fortsatte att diskuteras.
DSSO-listan är samma ordlista som man hittar på http://sv.speling.org/files/ (det görs en omdirigering till DSSO-sajten). Denna ordlista har även används i andra språk-/ordprojekt, t.ex.
* Visa ordklasser (presenteras i Svenska ordklasser samt gissning med hjälp av ordsuffix)
* Consonants Away (presentation i Consonants Away)
* samt ett gäng andra s.k. useless-projekt.
Posted by hakank at 09:50 FM Posted to Språk | Statistik/data-analys | Comments (7)
september 26, 2007
Videoföreläsning om R (del 1, en kort introduktion)
Decision Science News (en av favoritbloggarna kring beslutsteori, dataanalys etc) har nu börjat med videoföreläsningar i dataanalysverktyget R. Se vidare R video tutorial number 1. Det är en kort introduktion men kan vara början på något trevligt.
Som presentatören säger så rekommenderas en bok (eller två) i R (eller det mycet snarlika språket S). En förhoppningsvis fullständig lista över relaterare böcker finns här. Några av mina favoriter är:
* William N. Venables, Brian D. Ripley. S Programming (ISBN: 9780387989662). En introduktion för den som vill gå in på djupet i själva R-språket (eller S).
* William N. Venables, Brian D. Ripley: Modern Applied Statistics with S, 2002 (ISBN: 9780387954578). Det är en relativt avancerad bok men innehåller mycket matnyttig information, många tips och funktioner.
Se även Några videoföreläsningar om statistik, sannolikhet och data mining.
Posted by hakank at 10:31 EM Posted to Statistik/data-analys | Video podcasts | Comments (1)
augusti 21, 2007
Upptäcka kraftiga förändringar i tidsserier (changepoint detection)
I Recension av Keith Devlin, Gary Lorden: The Numbers Behind Numb3rs: Solving Crime with Mathematics nämndes att kapitel 4 When does the Writing First Appear on the Wall? - Changepoint Detection var det som gav mig mest ny information. Så naturligtvis har jag lekt lite med detta.
I Numb3rs-avsnittet Hardball (tredje säsongen) nämner Charlie Epps (matematikern i Numb3rs) Shiryayev-Roberts metod i samband med baseballresultat för att upptäcka förändringar i tidsserier, men den är "slightly more technical to describe" än den metod som E.S. Page skapade varpå man beskriver Pages. (Kapitlet är troligen skrivet av Gary Lorden eftersom han tidigare skrivit om changepoint detection. Och troligen är det E.S. Page paper "A test for a change in a parameter occurring at an unknown point" som avses. Men ingen av detta står uttryckligen i boken. Gnäll^2.)
Först presenteras kortfattat Pages metod, följt av min R-implementation. Hur väl den följer Page har jag faktiskt inte lyckats röna ut. Här används emellanåt "förändringspunkt" i stället för "changepoint"; "breakpoint" används också nedan.
Introduktion och beskrivning av Pages metod
En specifik händelse inträffar eller inte under en dag. Om den inträffar markeras detta i en tidsserie med 1, annars 0.
Bokens exempel är en händelse som inträffat c:a 1 gång per månad, dvs sannolikheten är 1/30. Sannolikheten för att händelsen inte inträffar är således 1-1/30 = 29/30. Detta är normalfallet. För att citera bokens lättsamma exempel på några sådana händelser som kan tänkas inträffa (i genomsnitt) en gång i månaden:
Examples abound - a New Yorker finds a parking place on the street in front of her apartment, a husband actually offers to take out the garbage, a local TV news show doesn't lead off with a natural disaster or violent crime, and so on.
Mer seriöst (och det beskrivs mer sådant i kapitlet) skulle man kunna tänka sig någon form av olycka eller sjukdomsfall som rapporteras varje dag. Notera att vi här endast arbetar med om händelsen inträffar eller inte; det är inte frågan om antalet olyckor etc. (Se i slutet av denna anteckning för hur man arbetar med numeriska värden.)
Vi vill nu upptäcka ("detektera") om/när det blir en drastisk förändring i hur ofta dessa händelser inträffar, t.ex. att de plötsligt inträffar i genomsnitt en gång i veckan i stället, dvs med sannolikheten 1/7. Låt oss kalla detta för extremfallet. Sannolikheten för att en extremhändelse inte inträffar en gång i veckan är således 1 - 1/7 = 6/7.
Falsklarm: Problemet med händelser som inträffar i genomsnitt en gång i månaden är att två händelser som i genomsnitt händer en gång i månaden faktiskt kan inträffa två intilliggande dagar eller klustra sig på andra sätt. Vi vill undvika falsklarm när slumpen gör det den ska (nämligen att slumpa).
Ett metod att minska antalet sådana falsklarm är alltså E.S. Pages metod som boken går igenom med ett exempel. Här har jag tagit beskrivningen från boken rakt av.
Det finns ett numeriskt index S som "spårar" aktiviteten dag för dag.
* Initialt är S = 1.
* För varje dag uppdateras värdet enligt följande:
- om händelsen inträffar under dagen: multiplicera S med sannolikheten för att
normalfalletextremfallet inträffar delat med sannolikheten förextremfalletnormalfallet inträffar, här (1/7) / (1/30) = 30/7 = 4.286 - om händelsen inte inträffar under dagen: multiplicera S med sannolikheten för att
normalfalletextremfallet inte inträffar delat med sannolikheten för attextremfalletnormalfallet inte inträffar, här (6/7) / (29/30) = 0.8867
- om S efter en sådan uppdatering blir mindre än 1: återställ S till 1
* Till slut finns ett gränsvärde för när vi ska varna för att en s.k. changepoint har inträffat. Om S överstiger detta gränsvärde anses händelserna nu komma en gång i veckan (extremfallet). I boken har man satt 50 som detta värde. (Det förs en liten diskussion hur olika gränsvärden påverkar hur väl man kan upptäcka förändringarna, men det går jag inte in på här.)
Bokens exempel
Boken använder följande händelsesekvens som exempel, dvs de första två dagarna inträffade händelsen inte, på tredje dagen inträffade den osv.
0 0 1 0 0 0 0 0 1
Från denna serie får man motsvarande S-värden (tänk på att S återställs till 1 om S < 1 och att S är 1 från början). De första två dagarna blir 1 enligt:
S * 0.8867 = 1 * 0.8867 = 0.8867 < 1, varpå S återställs till 1
Här är en liten tabell för att visa utvecklingen av S-värdet.
H S-värde
0 1
0 1
1 4.285714
0 3.800141
0 3.369583
0 2.987808
0 2.649287
0 2.349122
0 2.082965
1 8.926994
Inget av S-värdena är större än gränsvärdet (50), så ingen varning utfärdas för dessa första 10 dagar. Om händelsen inträffar även nästa dag (dag 11) skulle S-värdet vara 38.25854 (8.926994*4.285714) vilket inte heller ger någon varning. Om den även inträffar påföljande dag (dag 12) skulle det en varning utfärdas eftersom 8.926994*4.285714*4.285714 = 163.9652 >= 50.
Poängen med Pages S-serie är att den stiger kraftigt om händelsen inträffar, men avtar långsamt om händelsen inte inträffar. (Eller snarare: i detta exempel är det "kraftigt", det exakta beteendet beror på de specifika sannolikheterna.)
R-funktionen changepoint
Pages metod har implementerat i statistikpaketet R med följande funktion:
changepoint <- function(x,normal=1/30,non.normal=1/7,detect.value=50,plot=T){
occurs <- non.normal/normal # händelsen inträffar
not.occurs <- (1-non.normal)/(1-normal) # händelsen inträffar inte
S <- 1
vec = NULL # vektor med S-värdena
len <- length(x)
alerted <- FALSE;
cp <- NULL; # changepoint
S.cp <- 0; # värdet för S i changepoint
for (i in 1:len) {
obs <- x[i] # observationen
# justera S enligt metoden:
S <- ifelse(obs, S*occurs, S*not.occurs)
S <- ifelse(S<1,1,S) # reset om mindre än 1
# varna om S-värdet överstiger gränsvärdet
if (plot && !alerted && S >= detect.value) {
cat("Alert! observation #", i, ": ", S, " >= ", detect.value,"\n")
cp <- i; S.cp <- S; alerted <- TRUE
}
vec <- c(vec,S)
}
csum <- cumsum(x) # kummulativa summan av händelseserien
cumsum.val <- 0 # antal observationer
if (!is.null(cp) && cp > 0) { cumsum.val <- csum[cp] }
m<-max(csum) # för grafen
vec.len <- length(vec)
# plotta tre grafer
if(plot) {
op <- par(mfrow=c(3,1)) # plotta grafer
plot(x,type="l",
main=paste("Changepoint value: ", cp, " S-value:", round(S.cp,2) ))
if (!is.null(cp) && cp>0) { lines( rep( cp, 2), 0:1, col="red") }
plot(csum,type="l", main=paste("Cumulative sum. Num obs.:",cumsum.val) )
if (!is.null(cp) && cp>0) { lines( rep( cp, m+1), 0:m, col="red")}
plot(vec,type="l",main=paste("S values. Detect value: ", detect.value) )
abline( rep(detect.value, vec.len), 0:vec.len,col="red")
par(op)
}
# returvärde
list(vec=vec,cp=cp,cumsum.val=cumsum.val);
}
Funktionen har följande argument, där defaultvärdena är bokens exempel.
x: en vektor av respektive dagars värden om händelsen inträffade eller inte (1 eller 0)
normal:. Sannolikheten för att normalfallet inträffar, default 1/30 för att följa boken
non.normal: Sannolikheten för att extremfallet inträffar, default 1/7
detect.value: gränsvärde för changepoint-varning (default 50)
plot: huruvida man ska plotta respektive skriva ut en varning (när man gör flera simuleringar vill man inte att det plottas och håller på).
Följande värden returneras :
vec: vektor med S-värdena
cp: changepoint, dvs den observation där S-värdet överstiger varningsvärdet
cumsum.val: vilket är summan av antalet händelser som inträffat vid changepoint (egentligen endast för att jag ville kolla lite)
När man kör programmet visas tre grafer om man inte angivit plot=F i funktionen (visas nedan).
1) Först händelsegrafen, med 0 för ej inträffad och 1 för inträffad händelse. Den lodräta röda linjen visar changepointen om sådan finns. "S-value" är S-värdet för changepoint.
2) En graf för det kumulativa antalet inträffade händelser, samt en röd lodrät linje för changepoint. "Num. obs" är det antalet inträffade händelser för changepoint.
3) Den tredje grafen visar S-värdena. "Detect value" är gränsen för S-värdet (dvs då man ska slå larm) och visas som en röd vågrät linke. Notera att det kan vara svårt att se linjen om största S-värde är stort.
Körning av R-koden
Här är bokens exempel:
> x = c(0,0,1,0,0,0,0,0,0,1)
> changepoint(x, 1/30, 1/7, 50, T)
$vec
[1] 1.000000 1.000000 4.285714 3.800141 3.369583 2.987808 2.649287 2.349122
[9] 2.082965 8.926994
$cp
NULL
$cumsum.val
[1] 0
Som vi såg tidigare blev det alltså ingen changepoint eftersom S-värdet inte översteg 50. cp är därför NULL och antalet händelser vid changepoint är därför 0.
Graferna ser ut på följande sätt:
Ett mer intressant exempel (slumpat)
Här är ett mer intressant exempel. Det är en längre sekvens som jag helt enkelt slumpar fram med utgångspunkt från exemplets förutsättningar (normalfall resp. extremfall man vill detektera). I ärlighetens namn körde jag funktionen tills det blev en tidsserie med en changepoint.
För de första 30 dagarna inträffar händelsen (1) med sannolikheten 1/30, sedan kommer 30 dagar med sannolikheten 1/7 för 1. Här är slumpfunktionen:
c(sample(0:1,30,prob=c(29/30,1/30),rep=T),sample(0:1,30,prob=c(6/7,1/7),rep=T));
Så kör vi!
> x <-c(0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,1,1,0,0,
0,0,0,0,0,0,0,0,0,0,1,0,1,0,0,1,0,0,0,1,0,0,0,0,0,0)
> changepoint(x)
Alert! observation # 47 : 168.0480 >= 50
$vec
[1] 1.000000 1.000000 1.000000 1.000000 1.000000 1.000000
[7] 1.000000 1.000000 1.000000 1.000000 1.000000 4.285714
[13] 3.800141 3.369583 2.987808 2.649287 2.349122 2.082965
[19] 1.846964 1.637702 1.452150 1.287621 1.141732 4.893139
[25] 4.338744 3.847162 3.411277 3.024778 2.682069 2.378189
[31] 10.192239 43.681023 38.731942 34.343594 30.452447 27.002170
[37] 23.942811 21.230079 18.824700 16.691853 14.800657 13.123736
[43] 11.636810 10.318354 44.221515 39.211196 168.047983 149.008064
[49] 132.125377 566.251614 502.095027 445.207413 394.765194 1691.850832
[55] 1500.163299 1330.194059 1179.482416 1045.846478 927.351557 822.282168
$cp
[1] 47
$cumsum.val
[1] 6
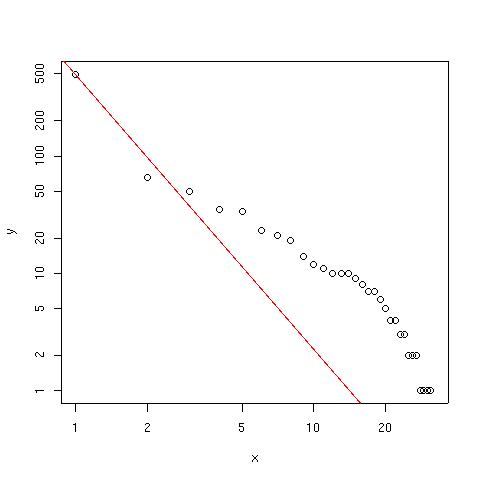
Kommentar: Här ser vi alltså att det blev en varning vid observation #47 (dag 47) och då hade händelsen inträffat totalt 6 gånger. Det var på den 16 dagen (31 + 16 = 47) efter att "extremfallet" började gälla (dvs med 1/7 som sannolikhet). Man kan f.ö. notera att just i denna sekvens blev det 2 stycken händelser efter varandra precis i början på "extremfallet".
Grafen för detta exempel:
Not: Om man kör programmet på ovanstående sätt, dvs batchar hela serien på en gång, så förfelar det sitt syfte. Man ska naturligtvis köra programmet varje dag efter man fyllt i dagens "händelsevärde" och kontrollera om det kommer en varning. Programmet fortsätter alltså att köra efter varningen. I stället borde kanske lampor i lustiga färger börja blinka, sirener börja tjuta och den stora valvdörren börjar stängas så att man måste skynda sig in i valvet innan dörren stängs helt med ett tungt och djupt "swoonk". Minsann kommer där en jeep i högsta fart genom stängslet och fyra personer rusar fram till dörren. Kommer de att klara sig? Ojoj, vad spännade det är...
Andra changepoint-metoder
Pages metod (enligt bokens förklaring och exempel i alla fall) hanterar endast binära tidserier (0/1). Det finns även metoder som detekterar changepoints i tidsserier med numeriska värden. Här nämns några R-funktioner.
Ett standardexempel är datamängden Nile: (via ?Nile i R) Measurements of the annual flow of the river Nile at Ashwan 1871-1970. Det intressanta med denna tidsserie är att år 1898 minskade flödet drastiskt eftersom man byggde första Ashwan-dammen. Kan denna förändring uppptäckas med changepoint detection-metoderna (även kallad "change point analysis", "change detection" etc). Svaret är naturligtvis jakande.
R-paketet struccchange
Med functionen breakpoints() i paketet strucchange visas flera olika changepoints (benämns breakpoints och breakdates för respektive observationsnummer och årtal). Brytpunkterna sorteras på hur stora (viktiga) de är. Nedan ser man att observation 28 (år 1898) är den viktigaste förändringspunkten; det hände också något vid observation 83 (år 1953) etc.
> library(strucchange)
> data(Nile)
> summary(breakpoints(Nile~1))
Optimal (m+1)-segment partition:
Call:
breakpoints.formula(formula = Nile ~ 1)
Breakpoints at observation number:
m = 1 28
m = 2 28 83
m = 3 28 68 83
m = 4 28 45 68 83
m = 5 15 30 45 68 83
Corresponding to breakdates:
m = 1 1898
m = 2 1898 1953
m = 3 1898 1938 1953
m = 4 1898 1915 1938 1953
m = 5 1885 1900 1915 1938 1953
Fit:
m 0 1 2 3 4 5
RSS 2835156.750 1597457.194 1552923.616 1538096.513 1507888.476 1659993.500
BIC 1318.242 1270.084 1276.467 1284.718 1291.944 1310.765
R paketet bcp
Ennan metod är funktionen bcp() från paketet bcp (Bayesian Change Point) som visar sannolikheterna för att de olika observationerna är en förändringspunkter. Den mest sannolika punkten har markerats med ett gäng utropstecken.
> library(bcp)
> Nile.bcp <- bcp(Nile)
> summary(Nile.bcp)
> Nile.bcp
Probability of a change in mean, Posterior Mean,
and SD for each position:
Probability Mean SD
1 0.016 1085.8 14.15
2 0.012 1085.6 14.06
3 0.014 1085.1 13.61
4 0.018 1085.5 13.80
5 0.018 1085.2 14.49
6 0.026 1084.8 15.67
7 0.046 1079.2 37.90
8 0.038 1089.4 29.73
9 0.062 1093.0 40.96
10 0.058 1082.8 26.11
11 0.028 1075.1 25.60
12 0.016 1072.0 27.79
13 0.016 1071.6 27.32
14 0.010 1071.0 28.02
15 0.022 1070.6 28.80
16 0.026 1069.5 30.92
17 0.022 1070.0 30.39
18 0.044 1067.7 38.25
19 0.088 1071.5 35.46
20 0.062 1084.1 29.90
21 0.054 1091.7 29.46
22 0.038 1098.5 31.98
23 0.026 1102.0 32.26
24 0.024 1104.9 34.27
25 0.028 1105.3 36.10
26 0.136 1102.9 36.36
27 0.184 1071.1 77.60
28 0.618 1029.3 108.61 !!!!
29 0.078 869.8 66.26
30 0.034 856.8 40.52
31 0.042 852.5 28.16
32 0.020 849.5 14.42
33 0.022 850.4 14.29
34 0.008 849.9 14.03
35 0.018 849.6 14.19
36 0.018 850.2 14.20
...
Den 28:e observationen har alltså högst sannolikhet. Den sista observationen har sannolikhet 1 och som jag ignorerar. En graf plottas också där man tydligt ser förändringen.
> which.max(Nile.bcp$posterior.prob[-c(100)])
[1] 28
> plot(Nile.bcp)
(För övrigt är detta blogganteckning #1200. Yeay!)
Uppdatering
Håkan Karlsson (aka hakke) uppmärksammade uppmärksamt att "normalfallet" och "extremfallet" hade förväxlats i pratbeskrivningen av hur S uppdateras. Tack hakke.
Posted by hakank at 07:39 EM Posted to Statistik/data-analys | Comments (2)
juli 03, 2007
Några videoföreläsningar om statistik, sannolikhet och data mining
Semester och det blir naturligtvis lite "hängmatte", t.ex. i form av videoföreläsningar.
Så här är några föreläsningar att förgylla sommaren med:
Davis Mease: Statistical Aspects of Data Mining
David Mease om "Statistical Aspects of Data Mining" med R (www.r-project.org) och Excel. Mease har detta även som en "riktig" (IRL inte bara URL) kurs med kurssajten www.stats202.com. Det är lugnt tempo som går igenom grunderna i både teori och verktyg.
Statistical Aspects of Data Mining (Stats 202) Day 1
Statistical Aspects of Data Mining (Stats 202) Day 2
I skrivande stund har endast publicerats ovanstående två föreläsningar. Efterkommande borde dyka upp via denna sökning på video.google.com .
Kursbok är Tan, Steinbach, Kumar: Introduction To Data Mining (ej läst).
Peter Donnelly: How juries get fooled by statistics
Peter Donnelly How juries get fooled by statistics. Visar flera av våra ointuitioner som finns inom området, ofta underhållare på ett traditionellt brittiskt-Grants sätt. Finns även på TEDTalks här.
Beskrivning:
Oxford mathematician Peter Donnelly explores the common mistakes we make in interpreting statistics, and the devastating impact these errors can have on the outcome of criminal trials. Statistical uncertainty and randomness, he says, confound many of our assumptions about the world. He shares the case of a British woman wrongly convicted of murdering her two infants -- a verdict reached, in part, by the misuse of statistics.
[För den som vill läsa mer t.ex. om det där mynt-experimentet finns en relativt djupgående redogörelse i Anirban DasGupta: Sequences, Patterns and Coincidences (PDF).]
Brian Brushwood: Scams, Sasquatch, and the Supernatural
Brian Brushwood Scams, Sasquatch, and the Supernatural. Är mest om debunkning av olika typer av pseudo-vetenskap, men innehåller en akt om sannolikheter (sammanträffanden). Underhållande och med högt tempo.
Ever wonder how those guys on TV seem to talk to the dead? What about ESP and psychic surgery? How do street scams and cons work? Want to ... all » know how YOU can trick your friends into believing you have psychic powers?As a magician, Brian’s wise to all the tricks used by frauds, tricksters, and con artists …and now he’s ready to take YOU to scam school. This is no ordinary lecture: we’re talking hands-on experiments, a live performance of psychic surgery, free giveaways of cash and prizes, and all the secrets TV psychics DON’T want you to know.
Topics covered include: scams, cons, ESP, UFOs, skeptic, skepticism, dowsing, astrology, memory, alternative medicine, psychic surgery, pseudoscience, coincidence, and crop circles.
Relaterat
Persi Diaconis On Coincidence (som jag iofs skrev om för några år sedan men rekommenderar gärna igen).
Talks Hans Rosling: New insights on poverty and life around the world
Talks Hans Rosling: Debunking third-world myths with the best stats you've ever seen
En kul semesterövning är att analysera lottodata från det sydafrikanska lotteriet. Se vidare bloggen Freakonomics: Is the South African Lottery Rigged? A Hands-On Exercise for Bored Blog Readers.
Uppdatering
Äh, jag glömde ju Scott McClouds grafiska novella The Right Number:
The Right Number is a projected three part online graphic novella about math, sex, obsession and phone numbers presented in an unusual zooming format. Click above to read Parts One and Two. (Part Three will hopefully be completed and available before too long.)
(Not: Serien är skriven 2003 så frågan är om det kommer en tredje del. De två första delarna är dock ganska självständiga. Via EconLog.)
(Avslutningsvis - men egentligen helt orelaterat till ovanstående - kan noteras att det för några veckor sedan var 4-årsdagen av denna bloggs födelse, som inträffade helt utan några virtuella tårterier. Referens till tidigare bemärkelseskriverier finns i förra årets 3-årsdag samt en drapa om varför bloggar bör ses som mer än en dagbok.)
Posted by hakank at 10:56 FM Posted to Sammanträffanden | Statistik/data-analys | Video podcasts
februari 11, 2007
Några länkar om dataanalys, data mining etc 20070211
Statistical Modeling, Causal Inference, and Social Science
The fallacy of the one-sided bet (for example, risk, God, torture, and lottery tickets)
Animated Social Network Visualization
Data Mining Research
Data mining application: terrorism, som även tipsar om en ny bok Data Mining and Predictive Analysis: Intelligence Gathering and Crime Analysis (ISBN: 075067796) skriven av Colleen McCue .
Geeking with Greg
Excellent data mining lecture notes tipsade för länge sedan om kursen CS345, Autumn 2006: Data Mining. Där finns en mängd presentationer av metoder.
Cognitive Daily
Is 17 the "most random" number?
Randomness wrap-up
Nyupptäckta bloggar i ämnet
Data Mining Research tipsade även om en ny blogg Crime Analysis and Data Mining: A meeting place for those interesting in analyzing or solving crimes using Predictive Analytics!, se presentationen.
Posted by hakank at 10:37 FM Posted to Machine learning/data mining | Statistik/data-analys
februari 04, 2007
Ultimate Research Assistant (Web Edition)
Ultimate Research Assistant (Web Edition) är en trevlig (men tyvärr långsam) applikation för att sammanställa sökresultat på ett mer intelligent sätt än de sökmotorerna. Systemet listar ut fraser som anses vara signifikanta för sökordet och visar representativa sajter
Exempel: sökning på "blogg" ger följande nyckelord.
- blogg
- att det
- jag har
- att jag
- blogg
- Climate Change
- det som
- för att
- har jag
- jag har
- om att
- om det
- Om man
- som jag
Av ovanstående fraser anses denna blogg vara representativ för flera: "att det", "jag har", "att jag", "om det", "det som", "om man", "som jag". Vilket kan få en att undra...
Vad gäller urvalet av fraser kan man möjligen anta att stackarn blivit förvirrad av innehållet av de 50 första sökresultaten av "blogg" på Yahoo!, eller så är det helt enkelt att - som det heter på julafton - att "Tony förstår inte språket så bra". Intressant nog finns "Climat Change" med, en het potatis i både inom och utanför bloggvärlden.
Sökningar på mer stringenta fackfraser såsom "text mining" (som råkar vara den teknik som Ultimate Research Assistant använder) och "Diaconis" (en husgud som ofta används för testning av sökverktyg) ger betydligt bättre resultat och känns användbart.
Man bör dock notera den brasklapp som står på sajten: It is an experimental proof-of-concept prototype, and should not be used for any official purposes.
Se vidare
Andy Hoskinson:
Creating the Ultimate Research Assistant där tekniken bakom verktyget förklaras.
Samme Hoskinson har även skapat verktyget Keyword Analysis Tool - Advanced Keyword and Keyphrase Extraction Technology for Content Analysis and Search Engine Optimization (SEO).
Wikipedia: Text mining
Tyvärr koms det här även att tänkas på 200 dagar som bl.a. visar förekomsterna av ord på hakank.blogg där ordet "jag" kom på fjärde plats, samt "jag" i bloggen där vidare språkanalyser genomfördes.
(Verktyget funnet via webbserverloggen.)
Posted by hakank at 05:46 EM Posted to Språk | Statistik/data-analys | Comments (4)
januari 26, 2007
The Blog Authorship Corpus
Den som har lust att göra dataanalyser på engelskspråkiga bloggtexter bör kika på The Blog Authorship Corpus:
The Blog Authorship Corpus consists of the collected posts of 19,320 bloggers gathered from blogger.com in August 2004. The corpus incorporates a total of 681,288 posts and over 140 million words - or approximately 35 posts and 7250 words per person....
The corpus may be freely used for non-commercial research purposes.
Zipfilen (nedladdningsbar via ovanstående sida) är 305Mb. Datan uppackad är 840 Mb, bestående av 19320 XML-filer med enkelparsrade taggar såsom <Blog>, <date>, <post>.
Kodningen av författarna görs i filnamnet, t.ex.
3802222.female.13.Student.Gemini.xml, dvs löpnummer, kön, ålder, sysselsättning samt stjärntecken (!).
Det görs en analys i J. Schler, M. Koppel, S. Argamon and J. Pennebaker Effects of Age and Gender on Blogging .
Via Data Mining: Text Mining, Visualization and Social Media
(Det vore trevlig med motsvarande corpus av svenska bloggtexter. Och hellre YYYYMMDD-födelsedata än stjärntecken.)
Posted by hakank at 07:32 FM Posted to Blogging | Statistik/data-analys | Comments (3)
januari 15, 2007
Hur mycket kan man sänka världsrekorden? (extremvärdesanalys)
Daily Time-artikeln World record in 100 metres can be lowered, study predicts diskuterar hur mycket nuvarande världsrekord bör kunna sänkas i olika sportgrenar. Analysen är gjord med den statistiska metoden extremvärdesteori (extreme values).
The world record in the 100-metre sprint can be lowered by another half-second before man reaches his limits, according to an expert in the field of extreme values. The men will hit a wall when Asafa Powell’s current record of 9.77 seconds mark is reduced to 9.29, a study by Prof John Einmahl of Germany’s Tilberg university predicted on Thursday....
Den undersökning som diskuteras är John Einmahl, Jan R Magnus: Records in athletics through extreme-value theory (PDF). Från inledningen:
How fast can humans or cheetahs run? What is the total (insured) loss of hurricane Katrina? Is a specific runway at JFK airport long enough for a safe landing? How high should the Dutch dikes be in order to protect us against high water levels? How long can we live? These questions all relate to extremes. In this paper we shall be interested in two questions on extremes relating to world records in athletics. The first question is: what is the ultimate world record in a specific athletics event
(such as the 100m for men or the high jump for women), given today's state of the art? Our second question is: how `good' is a current athletics world record? An answer to the second question will enable us to compare the quality of world records in diffrent athletics events.
På sidan 12 finns en fin tabell Ultimate world records, their precisions, and the current world
records återspeglad här nedan. Dvs det nuvarande världsrekordet på 100m (män) är 9.77. Enligt analysen ska man kunna pressa ner detta till 9.29.
| Men | Women | |||||
| Event | endpoint | precision | world record | endpoint | precision | world record |
| 100m | 9.29 | 0.39 | 9.77 | 10.11 | 0.40 | 10.49 |
| 110/100m h. | 12.38 | 0.35 | 12.88 | 11.98 | 0.19 | 12.21 |
| 200m | 18.63 | 0.88 | 19.32 | 20.75 | 0.57 | 21.34 |
| 400m | - | - | 43.18 | 45.79 | 1.83 | 47.60 |
| 800m | 1:39.65 | 1.44 | 1:41.11 | 1:52.28 | 1.39 | 1:53.28 |
| 1500m | 3:22.63 | 3.31 | 3:26.00 | 3:48.33 | 2.78 | 3:50.46 |
| 10,000m | - | - | 26:17.53 | - | - | 29:31.78 |
| marathon | 2:04:06 | 57 | 2:04:55 | 2:06:35 | 10:05 | 2:15:25 |
| shot put | 24.80 | 1.25 | 23.12 | 23.70 | 0.86 | 22.63 |
| javelin throw | 106.50 | 10.30 | 98.48 | 72.50 | 2.99 | 71.70 |
| discus throw | 77.00 | 2.85 | 74.08 | 85.00 | 8.10 | 76.80 |
| long jump | - | - | 8.95 | - | - | 7.52 |
| high jump | 2.50 | 0.05 | 2.45 | 2.15 | 0.05 | 2.09 |
Mer om detta
Econometrists Tilburg University Calculate the Ultimate Athletics Records
Den data som används i undersökningen finns tillgänglig från:
* Track Field Athlectics (Hans-Erik Pettersson)
* International Association of Athletics Federations (IAAF)
Mer om den extremvärdesanalys samt introducerande litteraturreferenser finns i Extremvärdesanalys av webbesök.
Posted by hakank at 05:39 EM Posted to Sport, idrott, hälsa | Statistik/data-analys | Comments (1)
oktober 29, 2006
Dagslänkar 2006-10-29 - tema lotterier
Maths theory bags lotto jackpot, via Minding the Planet
CBC News: Lottery retailers enjoying luck of the draw: Fifth Estate probe, via Sabermetric Research
Och varför inte de något relaterade
Lite om konsekutiva talpar i Lotto (och dess varianter).
Littlewood's Law of Miracles -The law of truly large numbers
Posted by hakank at 06:47 FM Posted to Statistik/data-analys
rcompletion: Tab-komplettering i R
I statistik- och dataanalyspaketet R har det funnits tab-kompletteringar (för kommandoradsvarianten) men endast för filnamn. Länge har jag saknat att kunna tab-komplettera funktionsnamn à la Emacs eller Unix-skal.
I morse - i loggen över icke automatinstallerade paket - hittades paketet rcompletion som gör precis detta. Det är inte bara variabelnamn och funktionsnamn som kompletteras, utan man kan även få fram parametrarna i en funktion. Det sistnämnda känns mycket användbart.
En första not
rcompletion funkar endast för kommandoradsversionen av R och endast på system som har libreadline. Se nedan hur man installerar paketet, jag hade nämligen lite problem med detta.
Några exempel
Vi börjar med att ladda in paketet tseries för att testa lite
> library(tseries)
Så börjar vi vår tab-session, där <TAB> alltså betyder tab-tangentens nedtryckande.
> ari<TAB>
som ger följande förslag:
arima( arima0( arima0.diag( arima.errors( arima.sim(
Varpå vi sedan tabbar inom en funktion, dvs inklusive första parentesen och får listan över funktionens parametrar.
> arima(<TAB>
fixed = kappa = n.cond = seasonal = xreg =
include.mean = method = optim.control = transform.pars =
init = model = order = x =
Nifty!
Mixtrande med installationen av rcompletion (version 0.8) hos mig
Tyvärr så var jag tvungen att mixtra lite för att kunna installera paketet. Anledningen till att det inte gick in vid automat-installationen (via R:s normala install.packages()) var att konfigurationen inte tyckte att min dator har libreadline.so, vilket ju är väldigt felaktigt.
Varpå följande gjordes:
1) ladda ner paketfilen (via paketets sida sida)
2) manuellt packa upp paketfilen i lämplig katalog (tar zxcv paketnamnet)
3) i katalogen som skapades finns filen configure. På ungefär rad 2287 (för version 0.8) finns dessa rader som utan pardon kommenterades bort enligt följande:
# if test $ac_cv_lib_readline_rl_completion_matches = yes; then
PKG_CFLAGS="${PKG_CFLAGS} -DHAVE_LIBREADLINE"
PKG_LIBS="${PKG_LIBS} -lreadline"
#else
#
# { { echo "$as_me:$LINENO: error: readline is required but was n\ ot found" >&5
#echo "$as_me: error: readline is required but was not found" >&2;}
# { (exit 1); exit 1; }; }
# exit 1
#
#fi
dvs raderna med PKG_CFLAGS och PKG_LIBS ska vara kvar.
4) efter detta installerar man paketet manuellt (eventuellt som root om R är så installerat).
R CMD INSTALL paketnamn
5) I R laddar man paketet som vanligt med library(rcompletion)
Paketförfattaren är medveten om att det finns problem och skriver mer här.
Uppdatering torsdag 11 nov 2006
Installationsproblemet ser ut att ha löst sig. Paketet installeras nu helt sömlöst.
Posted by hakank at 06:22 FM Posted to Statistik/data-analys
juni 08, 2006
Vilken boll är rundast? Slumpmässighet i sporter
I P1 pratades precis om att fotboll är den mest slumpmässiga sporten. Matematikern som intervjuades, Torbjörn Lundh, har skrivit Which ball is the roundest? – a suggested tournament stability index (PDF).
Abstract:
All sports have components of randomness that team not to win every game. According to many spectators of the charm when following a competition or a match. less of this unpredictability? We suggest here a general stability index, which could measure this randomness factor and different sports. As an illustration we use exemplify squash, and soccer. Results will also be given on tournaments football, ice-hockey, and handball. Furthermore, we will optimization questions that turned up on the way.
(Funnen via sidan Vetenskapsfestival 2006)
Uppdatering
Intervjun kan (förhoppningsvis) ålyssnas via följande djuplänk.
Malin på Vetenskapsnytt skrev i vintras (onsdag, januari 04, 2006) om en liknande undersökning: Fotboll är den mest spännande sporten, säger forskare, där följande paper omnämns:
E. Ben-Naim, F. Vazquez, S. Redner What is the most competitive sport? (arXiv.org)
We present an extensive statistical analysis of the results of all sports competitions in five major sports leagues in England and the United States. We characterize the parity among teams by the variance in the winning fraction from season-end standings data and quantify the predictability of games by the frequency of upsets from game results data. We introduce a mathematical model in which the underdog team wins with a fixed upset probability. This model quantitatively relates the parity among teams with the predictability of the games, and it can be used to estimate the upset frequency from standings data. We propose the likelihood of upsets as a measure of competitiveness.
Andra bloggar om: matematik, sport.
Posted by hakank at 07:42 FM Posted to Matematik | Sport, idrott, hälsa | Statistik/data-analys | Comments (3)
januari 23, 2006
Något om prefixträd sorterade på lite olika sätt samt komprimering
Av en privat (och personlig) orsak behövdes ett program för att skapa unika prefix av ord i en lista, och sedan att presentera dessa prefix som ett träd. Anledningen var ungefär att korta ner en lista av ord till kortare ord (dess prefix).
Ett exempel på ett sådant prefixträd är för de svenska månadsnamnen:
a:
ap: april
au: augusti
d: december
f: februari
j:
ja: januari
ju:
jul: juli
jun: juni
m:
ma:
maj: maj (!!!)
mar: mars
n: november
o: oktober
s: september
Här ser vi t.ex. att månadsnamnen december, februari och november kan komprimeras till en enda bokstav, medan april och augusti båda börjar på bokstaven a så vi måste här ta till en extra bokstav för att skilja dem åt. Man kan också notera att maj inte blev något prefix alls, utan här behövs hela ordet eftersom mars, den rackaren, ligger och stör. Sådana fall markeras med !!!!
Program Prefix Trees
Det har naturligtvis skapats ett program för att kunna leka vidare med sådana här ord-listor, och som - möjligen något missledande - kallas för Prefix trees.
Programkörningen för ovanstående svenska månadsnamen finns ungefär här.
Komprimering och annat skoj
Även om det primära syftet med programmet var att skapa unika prefix och prefixträd så var det svårt att låta bli att studera vissa saker i mer detalj.
Om man kör programmet för de svenska månadsnamnet kommer det, förutom det fina prefixträdet, även lite statistik (längst ner på sidan):
...
Original total length of words: 74
Total length of prefixes: 23
Mean prefix length: 1.92
Compression factor (original length/prefix length): 3.217
Man kan bl.a. se att det medellängden av de skapade prefixen är 1.92, vilket ska jämföras med medellängden av de ursprungliga orden på 6.17. Komprimeringsfaktorn är 3.217, vilket räknas ut med formeln
(sammanlagda längden av original orden) / (sammanlagda längden av prefixerna)
Dvs: genom att använda de unika prefixen istället för de hela orden sparar man en hel del, t.ex. träd (sic!) om man skulle använda papper för att skriva dem. Det kanske blir svårt att läsa det, men man skulle kunna spara både tid och pengar på detta. Nedan kommer vi att studera hur man kan spara något mer tid/papper/pengar men i gengäld blir det i stort sett oläsbart...
Frekvenssortering av bokstäver
En finess med programmet är att man kan studera lite olika varianter av representation av orden innan det skapas prefix. T.ex.
- bokstäverna i ordet sorteras innan man gör prefixen, valet Sort (plain)
- bokstäverna i ordet sorteras i omvänd ordning, valet Reverse. Not: om man både sorterar och reverse, blir det i omvänd sorteringsordning, dvs "ö" kommer före "ä" etc.
Sedan den mest intressanta varianten: bokstavsfrekvenssortering (valet Sort by letter frequency, som innebär att innan man skapar prefixen sorterar man ordets bokstäver i ordning av hur vanliga/sällsynta bokstäverna är bland samtliga ords bokstäver. T.ex. så är det troligt att bokstaven "z" är sällsynt vilket gör att ett ord med "z" kommer att prefixas som z + eventuellt någon annan bokstav.
Om vi fortsätter med månadsnamnsexemplet får man med bokstavsfrekvenssortering följande prefixträd:
d: december
f: februari
g: augusti
j: maj
k: oktober
l: juli
n:
nj:
nju:
njui: juni
njuia: januari
p:
pl: april
ps: september
s: mars
v: november
....
Original total length of words: 74
Total length of prefixes: 21
Mean original length: 6.17
Mean prefix length: 1.75
Compression factor (original length/prefix length): 3.524
Om man jämför med det "vanliga" prefixträdet så är komprimeringsfaktorn något lägre för bokstavsfrekvenssorteringsvarianten (3.524 jämfört med 3.217).
Denna skillnad tenderar att vara beständigt: Detta innebär att om man använder bokstavsfrekvenser istället blir det något bättre komprimering. Nackdelen är naturligtvis att "förkortningen" (prefixet) är fullständigt obegriplig. Se även en mer systematisk genomgång nedan.
Några noter kring detta
Möjligen skulle man här kunna göra en analogi med Huffman-kodning (ref till en.wikiedia) som skapar binära koder efter bokstävernas frekvens, där den kortaste koden tilldeleas den vanligaste bokstaven etc.
En mer avancerad variant av prefixträd skulle vara att analysera prefixträdet för att komprimera det ännu mer.
Det går naturligtvis också att göra det väldigt enkelt för sig och koda varje ord till ett eller flera fullständigt slumpmässiga tecken alltefter ordens/bokstävernas frekvens i texten. Men det är en övning som lämnas åt vidare öden (eller övning åt läsaren/skribenten).
Den ursprungliga poängen med prefixträden var att de skulle vara lätta att skapa och (relativt) lätt att uttyda när man ser dem. När man använder sorteringar av olika slag förloras detta syfte bort i skymningen varvid endast nästa dags solstrålar är glada att se det.
Liten undersökning
Det gjordes också en undersökning hur antalet olika ord i listan påverkar komprimeringsfaktorn respektive medelprefixlängden. Detta gjordes för ett olika antal slupmässiga svenska ord (ur en ordlista på nästan 400000 ord).
Det visar sig - inte speciellt förvånande - att ju fler slumpmässiga ord listan innehåller, desto sämre blir komprimeringsfaktorn och desto längre blir medellängden på prefixen. Som variansen visar är det relativt stabila värden förutom för den första körningen (10 ord i listan). Av tidsskäl kördes endast 10 gånger med samma liststorlek.
Prefix utan någon bokstavssortering
| Antal ord | Komprimeringsgrad | Komprimeringsgrad varians | Prefix medellängd | Prefix medellängd, varians |
| 10 | 7.80730 | 4.67526 | 1.47000 | 0.12456 |
| 100 | 4.14080 | 0.02874 | 2.63700 | 0.00842 |
| 200 | 3.54860 | 0.03530 | 3.11500 | 0.01812 |
| 500 | 3.04260 | 0.00201 | 3.60800 | 0.00775 |
| 1000 | 2.70590 | 0.00199 | 4.10200 | 0.00368 |
| 2000 | 2.39940 | 0.00078 | 4.60200 | 0.00717 |
| 3000 | 2.23620 | 0.00063 | 4.96000 | 0.00207 |
| 5000 | 2.06810 | 0.00030 | 5.36400 | 0.00158 |
| 10000 | 1.84500 | 0.00009 | 5.99800 | 0.00057 |
| 20000 | 1.65400 | 0.00002 | 6.68800 | 0.00040 |
| 50000 | 1.44040 | 0.00001 | 7.68000 | 0.00031 |
| 100000 | 1.31520 | 0.00000 | 8.41300 | 0.00020 |
Prefix med frekvensbokstavssortering
| Antal ord | Komprimeringsgrad | Komprimeringsgrad varians | Prefix medellängd | Prefix medellängd, varians |
| 10 | 9.68830 | 4.15306 | 1.15000 | 0.02500 |
| 100 | 4.24470 | 0.02675 | 2.56800 | 0.01280 |
| 200 | 3.81910 | 0.02128 | 2.94800 | 0.00544 |
| 500 | 3.26520 | 0.00193 | 3.40900 | 0.00283 |
| 1000 | 2.89340 | 0.00351 | 3.83500 | 0.00372 |
| 2000 | 2.61810 | 0.00032 | 4.24200 | 0.00044 |
| 3000 | 2.47130 | 0.00082 | 4.48900 | 0.00159 |
| 5000 | 2.28780 | 0.00018 | 4.82100 | 0.00054 |
| 10000 | 2.06480 | 0.00009 | 5.36200 | 0.00042 |
| 20000 | 1.87310 | 0.00003 | 5.91000 | 0.00018 |
| 50000 | 1.65010 | 0.00001 | 6.70800 | 0.00008 |
| 100000 | 1.50710 | 0.00000 | 7.34400 | 0.00014 |
Andra exempel
Jag har även kört programmet på några andra exempel, t.ex. 1000 vanligaste svenska orden, svenska förnamnen samt svenska efternamnen (plus "Kjellerstrand") från Språkbanken:
- 1000 vanligaste svenska orden (inklusive siffror, årtal och delar av förkortningar)
- 1000 vanligaste svenska orden, sorterade enligt bokstavsfrekvens
- 1000 vanligaste svenska förnamnen
- 1000 vanligaste förnamnen, sorterade enligt bokstavsfrekvens
- 1000 vanligaste svenska efternamnen (plus "kjellerstrand")
- 1000 vanligaste svenska efternamnen, sorterade enligt bokstavsfrekvens (plus "kjellerstrand")
- 1000 slumpmässiga svenska ord.
- 500 slumpade svenska ord, utan sortering samt med bokstavsfrekvenssortering.
Se även
En möjlig variant att göra en komprimering eller på annat sätt förkorta saker och ting är att använda reguljära uttryck, t.ex. som i programmet MakeRegex,.
Posted by hakank at 10:51 EM Posted to Program | Språk | Statistik/data-analys | Comments (2)
oktober 29, 2005
Kritik kring power law-forskning
Några korta länkningar till en intressant kritik av power law-forskningen och speciellt av Albert-László Barabasi (som jag skrivit om en del tidigare).
Joao Gama Oliveira och Albert-László Barabási skrev nyligen Darwin and Einstein correspondence patterns (PDF, Complementary Materials). New Scientist skrev sedan om detta i Email and letter writing share fundamental pattern. Jämför med Barabasis The origin of bursts and heavy tails in human dynamics (PDF, dess Supplement) som undersöker hur mail skickas och besvaras mellan en flera personer.)
Här är några aktuella och tidigare kritiska röster kring power law-forskningen. "Huvudpersonerna" är två statistiska fördelningar:
Log normal
Power law
"Normal" som Shalizi skriver om i citatet nedan är Normal distribution.
Cosma Shalizi: Gauss Is Not Mocked:
[T]he apparent power law is merely an artifact of a bad analysis of the data, which which is immensely better described by a log-normal distribution....
Log-normals are very common, for the same reasons that normals are. Unlike normals, they are very easy to mistake for power law distributions, especially if your knowledge of statistics is as limited as most theoretical physicists'. (The distribution of links to weblogs, for instance, is much better fit by a log-normal than a power law, as we've seen.)
Cosma Shalizi: Speaking Truth to Power About Weblogs, or, How Not to Draw a Straight Line.
Daniel B. Stouffer, R. Dean Malmgren, Luis A. N. Amaral: Comment on Barabasi, Nature 435, 207 (2005)
Michel L. Goldstein, Steven A. Morris, Gary G. Yen: Problems with Fitting to the Power-Law Distribution
Aaron Clauset: Links, links, links.
Pharyngula: λ >> µ, or why I haven't answered you yet
Geomblog: Darwin's and Einstein's (e)mail correspondence rates, or a rumination on power laws.
Michael Mitzenmacher har skrivit en översikt över power-law-forskningen: A Brief History of Generative Models for Power Law and Lognormal Distributions (PDF, publicerad i Internet Mathematics, volume 1); en tidigare version PS), och berättar i en videoföreläsning sina egna åsikter om denna forskning: New Directions for Power Law Research, där själva videoströmningen (QuickTime) finns här. (Från Models of Real-World Random Networks med en massa andra intressanta videos.)
Se även B. Conrad and M. Mitzenmacher Power Laws for Monkeys Typing Randomly: The Case of Unequal Probabilities (PDF).
Posted by hakank at 10:03 FM Posted to Social Network Analysis/Complex Networks | Statistik/data-analys
augusti 29, 2005
Kortsamlarproblemet (coupon collector problem) i mindre och isolerade nätverk med fullständigt utbyte av kort
Introduktion
När jag var liten samlade jag en hel del på samlarkort, t.ex. flaggor, ishockey-/fotbollsspelare etc. Det var alltså sådana kort där man köpte osett, ett eller flera kort i en påse (med eventuellt medföljande tuggummi eller annat godis) och sedan antingen köpte man nya eller bytte man till sig de kort man inte hade. Den stora poängen var naturligtvis att få hela serien komplett. (Det fanns säkert en fin social poäng i att träffas och byta sådana kort, men sådana finesser uppfattade man nog inte i denna ålder, typ kring 10+ år.)
Speciellt för flaggorna kommer jag ihåg att det fanns vissa kort som var väldigt svåra att få tag på (var det Mexiko med nummer 104, eller kanske var det Kenya?). Om jag nu kommer ihåg detta korrekt var det några få lyckostar som fått detta kort och vi andra dräglade djupt över dessa rara kort.
Kortsamlarproblemet (coupon collector problem)
Det finns ett klassiskt problem inom statistiken/sannolikhetsläran som handlar om detta: kortsamlarproblemet (coupon collector problem, dvs kupongsamlarproblemet) där man studerar hur många kort man behöver köpa i genomsnitt (eller för en viss säkerhetsgrad) på att få samtliga kort i en sådan samlarserie. Det visar sig att det är ointuitivt många: För att få tag i samtliga kort i en serie av 100 kort behöver man i medeltal köpa 519 kort. (Enkel formel för detta : 100*sum(1/(1:100)) ~ 519, där 100 i formeln är just antal unika kort i samlarserien.)
Men detta antal fluktuerar naturligtvis: för att vara säker till 95% att få tag i samtliga kort krävs 791 inköpta kort. Se även min Simuleringssida för lite mer om detta; sök på "samlarkortproblemet ".
Man kan notera att ovanstående beräkningar endast gäller för en person som ensam inhandlar kort. Om man tillåter byte av kort är det en annan sak, och det är precis det som det följande kommer att handla om.
Samlarkortproblemet i ett isolerat nätverk med fullständigt utbyte
För ett tag sedan hade jag en diskussion med en kompis om detta. Denne - som vi kan kalla för E - hävdade att företagen troligen inte tillverkar lika många av varje kort, just för att få oss att köpa fler kort för att få tag i samtliga.
Denna konspirationsteori är möjligen korrekt, men jag började undra om denna effekt kunde uppstå även om företaget tillverkade lika många exemplar av alla kort, och att det vi råkat ut för var en "klustereffekt", dvs att de kort som vi i vårt lilla nätverk var en slumpmässigt urval med de traditionella egenskaperna hos sådana urval.
E antog att företagen som skapar korten alltså tillverkar vissa kort i färre upplagor, säg att de färsta (sic!) är en tiondel av de som tillverkas mest. Min utgångspunkt var att denna effekt skulle kunna vara subjektiv enligt "regeln" att om man slumpmässigt drar ett antal olikfärgade kulor från en påse med lika fördelning så är det mycket stor sannolikhet att något antal är färre än de övriga och att det finns en färg som dras fler gånger.
Detta är något man kan testa med en simulering. Vilket har gjorts.
Sammanfattning
Som vi kommer att se uppstår faktiskt denna typ av effekt (E-effekt) om det totalt köps in ett mindre antal samlarkort. För 700 inköpta kort blir förhållandet mellan minst antal kort och flest antal kort rätt exakt 1/10.
Här nedan kommer även andra saker att visas, t.ex. denna effekt hos Lotto-dragna nummer, där samma förhållande är 1/2, vilket även uppstår i en simulering. Kanske inte så remarkabelt men intressant.
Lokalt nätverk med fullständigt utbyte av samlarkort
Först en sak om nätverket. Den modell som vi här arbetar med innebär att det finns en mindre grupp, säg ett 10-tal personer, som har fritt utbyte av samlarkort inom gruppen men inte har något som helst kort-utbyte med några externa personer eller andra nätverk. Denna fullständiga isolering av inköpen gör modellen enkel att simulera.
(Man skulle även kunna studera komplexa nätverks-effekter kring detta, dvs att någon i Husieskolans krets känner någon i Stockholm och byter till sig de i Husie-kretsens ovanliga kort. Ju fler sådana svaga länkar mellan olika (inte helt isolerade) nätverk det finns, desto större blir naturligtvis den totala kretsen vilket leder till att denna lokala nätverkseffekt vi talar om här blir mindre.)
Modell och simulering
Tänk nu följande som översättning av samlarkortproblemet i ett lokalt nätverk till slumpmässig dragning av heltal i ett intervall.
En grundläggande förutsättning är att det faktiskt skapas exakt lika många kort, och att man globalt har lika stor chans att köpa alla kort, men vi studerar endast en mindre krets (nätverk) av personer som får tillgång till ett urval av dessa, t.ex. där tobakaffärens och den där kioskens urval.
Låt oss för enkelhetens skull anta att samlarkortserien har 100 olika kort. Dessa 100 olika korten motsvaras i simuleringen då av de första 100 positiva heltalen (1..100 alltså). Ett inköp av ett kort motsvarar att man slumpmässigt drar ett tal inom detta intervall, där alla tal har lika stor chans att dras. Detta görs s.a.s. med återläggning, så att ett tal har möjlighet att dragas igen.
Man drar slumpmässigt n stycken sådana tal, vilket alltså motsvarar inköp av n stycken samlarkort.
Efter det beslutade antalet "kort" (tal) är dragna, kontrolleras fördelningen bland dessa kort. Här jämför man antalet kort som kommit upp med minst antal och de som kommit med flest antal. Om ss är listan över de dragna talens fördelning är det sökta värdet alltså: min(ss)/max(ss), det som nedan kallas för min/max-förhållandet.
Vi behöver inte förutsätta något om hur stor gruppen är eller hur många kort en specifik deltagare införskaffar. Vi kommer senare se hur många fullständiga serier ett visst antal inköpta kort tenderar att generera, och man kan alltså anpassa antalet kort som (i medeltal) behöver köpas in för att få fullständiga serier.
Frågeställningen och hypotesen
Låt oss alltså se hur fördelningen mellan minimi-antalet kort och maximi-antalet kort utvecklas med det totala antal kort som inköpes.
Frågeställningen: Vad är förhållandet mellan min/max om det totalt köps in num.bought stycken kort av num.cards möjliga?
Hypotes: Om man slumpmässigt kommer fram till sådana min/max-förhållande på säg 1/10 eller något liknande har vi inget statistiskt stöd för E:s konspirationsteori.
Här följer R-koden som använts för simuleringen, som helt enkelt drar num.bought stycken tal ur intervallet 1..num.cards och returnerar fördelningen av de dragna talen (dvs hur många 1:or som dragits, hur många 2:or etc). Man kan här också notera hur enkelt denna simulering är. Det beror på att vi gjort det enkelt för oss och förutsatt att det fullständigt och fritt utbyte i detta isolerade nätverk.
collector.group.sim <- function(num.cards=100, num.bought=10000) {
ss <- rep(0,num.cards);
for (i in 1:num.bought) {
s <- sample(1:num.cards,1);
ss[s] <- ss[s] + 1;
}
ss
}
Exempel:
Om vi nu antar att det är 100 olika kort och 10 personer som samlar, samt att dessa vardera köper respektive 200 kort, inalles 10*200 = 2000 kort. En sådan simulering ser ut så här (sorterad lista eftersom vi inte behöver bry oss om de specifika talen/korten som dragits):
> ss<-collector.group.sim(100, 10*200);sort(ss);min(ss);max(ss);min(ss)/max(ss)
[1] 10 11 12 12 12 13 14 14 14 15 15 15 16 16 16 16 16 16 17 17 17 17 17 17 17
[26] 17 18 18 18 18 18 18 18 18 19 19 19 19 19 19 19 19 19 19 19 19 20 20 20 20
[51] 20 20 20 20 20 20 20 20 20 20 20 20 21 21 21 21 21 21 21 21 21 22 22 22 22
[76] 22 22 23 23 23 23 24 24 25 25 25 25 25 25 26 26 26 27 27 27 27 28 28 33 33
[1] 10
[1] 33
[1] 0.3030303
> 10*200
[1] 2000
Här kan vi alltså se att det minsta antalet dragna tal/kort är 10, dvs min(ss), och max är 33. Förhållandet mellan dessa min(ss)/max(ss) är 10/33 ~ 0.3. Redan enna enkla simulering (detta nätverk) ger en känsla av att vissa kort är ovanligare än varandra, och förhållandet mellan de ovanligaste och de vanligaste är 10 på 33.
Personligen tycker jag detta är emot intuitionen: efter en slumpmässig dragning har vi ett min/max-förhållande på så stort som 0.3.
Om vi istället säger att man tillsammans endast köper 519 kort (dvs så många som det i genomsnitt krävs för att en person ska få en komplett serie) får vi några intressanta resultat. Notera att även här är det endast en enda körning, för att få en känsla för datan.
> ss<-collector.group.sim(100, 519);sort(ss);min(ss);max(ss);min(ss)/max(ss)
[1] 1 1 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4
[26] 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 5 5 5
[51] 5 5 5 5 5 5 5 5 5 5 5 5 5 6 6 6 6 6 6 6 6 6 6 6 6
[76] 7 7 7 7 7 7 7 7 7 7 7 8 8 8 8 8 8 8 9 9 10 10 11 12 13
[1] 1
[1] 13
[1] 0.07692308
Här kan till exempel följande noteras:
* min/max-förhållandet är värre än E:s föreslags 1/10, nämligen 1/13 (0.077)
* det minsta talet är 1 vilket innebär att det finns kort för en fullständig serie. (Fullständiga serier kommer att studeras mer här nedan.)
Vi gör nu en mer statistisk korrekt simulering med 100 sådana här simuleringar och tar medelvärdet för min/max-förhållandet:
> mean(replicate(1000,{ss<-collector.group.sim(100, 519);min(ss)/max(ss)}))
[1] 0.05141527
min/max-talet 0.05 (~ 1/20) stödjer ovanstående känsla att det är värre min/max-förhålllande än E:s 1/10.
Men det är kanske inte så realistiskt att en grupp tillsammans köper endast 519 kort? Låt oss nu titta på hur min/max-förhållandet påverkas av antalet inköpta kort.
Tabell över (medelvärde) av min/max-förhållandet för olika antal kortinköp
Om vi nu studerar medelvärdet av min/max för olika antal kortinköp får man följande tabell.
Från 100 inköp till 3000
> sapply(1:30, function(n) rbind(n*100, mean(replicate(100,{ss<-collector.group.sim(100, n*100);min(ss)/max(ss)})) ))
[,1] [,2] [,3] [,4] [,5] [,6] [,7]
[1,] 100 200 300 400.00000000 500.00000000 600.00000000 700.0000000
[2,] 0 0 0 0.01154701 0.04447036 0.07848971 0.1029102
[,8] [,9] [,10] [,11] [,12]
[1,] 800.0000000 900.0000000 1000.0000000 1100.0000000 1200.0000000
[2,] 0.1298539 0.1475774 0.1695608 0.1864951 0.1996583
[,13] [,14] [,15] [,16] [,17]
[1,] 1300.0000000 1400.0000000 1500.0000000 1600.0000000 1700.0000000
[2,] 0.2132364 0.2434604 0.2501553 0.2677531 0.2798811
[,18] [,19] [,20] [,21] [,22]
[1,] 1800.0000000 1900.0000000 2000.0000000 2100.0000000 2200.0000000
[2,] 0.2819174 0.2909844 0.3101849 0.3119899 0.3260513
[,23] [,24] [,25] [,26] [,27]
[1,] 2300.0000000 2400.0000000 2500.0000000 2600.0000000 2700.0000000
[2,] 0.3373065 0.3520848 0.3504074 0.3622678 0.3721507
[,28] [,29] [,30]
[1,] 2800.0000000 2900.0000000 3000.00000
[2,] 0.3841707 0.3844286 0.38901
Här kan man se att gränsen för 1/10 i förhållande mellan min och max är cirka 700 inköp. Detta motsvarar en liten grupp på 7 personer som köper vardera 100 kort, eller 4 personer som köper 175 kort osv. Jag tycker att det låter rätt lite, men å andra sidan var E:s 1/10 taget ur luften.
Om vi tar lite större steg: mellan 1000 till 30000 inköp:
> sapply(1:30, function(n) rbind(n*1000, mean(replicate(100,{ss<-collector.group.sim(100, n*1000);min(ss)/max(ss)})) ))
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 1000.0000000 2000.0000000 3000.0000000 4000.0000000 5000.0000000 6000.0000000
[2,] 0.1684101 0.3033053 0.3869192 0.4466518 0.4883167 0.5158891
[,7] [,8] [,9] [,10] [,11] [,12]
[1,] 7000.0000000 8000.0000000 9000.0000000 10000.0000000 11000.0000000 12000.0000000
[2,] 0.5387887 0.5611546 0.5857873 0.6023973 0.6199602 0.6338816
[,13] [,14] [,15] [,16] [,17]
[1,] 13000.0000000 14000.0000000 15000.0000000 16000.000000 17000.0000000
[2,] 0.6371665 0.6508695 0.6613642 0.665185 0.6797338
[,18] [,19] [,20] [,21] [,22]
[1,] 18000.0000000 19000.0000000 20000.0000000 21000.0000000 22000.0000000
[2,] 0.6845181 0.6965812 0.6978221 0.7095483 0.7138271
[,23] [,24] [,25] [,26] [,27]
[1,] 23000.0000000 24000.0000000 25000.0000000 26000.000000 27000.0000000
[2,] 0.7187094 0.7274481 0.7267149 0.733775 0.7309658
[,28] [,29] [,30]
[1,] 28000.0000000 29000.0000000 30000.0000000
[2,] 0.7380007 0.7450008 0.7422353
Exempel: I vårt lilla samlarkortnätverk var vi väl 10 stycken och köpte kanske 150
kort per person, dvs total 10*150 = 1500 inhandlade kort. I tabellen ser man att
förhållandet mellan antalet färst kort och antalet flest kort är 0.25 (1/4), vilket
troligen skulle kunna uppfattas som den E-effekt vi talade om i början.
Ännu större inköp som tar riktigt lång tid att simulera: för 100000 inköpta kort blir medelvärdet av min/max cirka 0.85 (0.8506242). För en miljon inköp är det 0.9512054.
Vi ser alltså att min/max-förhållandet tenderar att utjämnas då antalet inköp ökar, vilket är vad man kan förvänta sig enligt de stora talens lag.
Fullständiga serier i nätverket
Ser man på minimivärderna för dessa får man antalet (genomsnittligt uppkomna) fullständiga serier i nätverket. Detta förutsätter alltså att alla i nätverket byter rakt av och inte är snikna eller har orealistiska byt-krav.
> sapply(1:30, function(n) rbind(n*1000, mean(replicate(100,{ss<-collector.group.sim(100, n*1000);min(ss)})) ))
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9]
[1,] 1000.00 2000.00 3000.00 4000.00 5000.0 6000.0 7000.00 8000.00 9000.00
[2,] 3.08 9.71 17.08 24.98 33.2 41.2 49.87 59.03 66.67
[,10] [,11] [,12] [,13] [,14] [,15] [,16] [,17]
[1,] 10000.00 11000.00 12000 13000.00 14000.00 15000.00 16000.00 17000.00
[2,] 76.01 84.79 94 102.37 111.52 120.41 128.45 138.62
[,18] [,19] [,20] [,21] [,22] [,23] [,24] [,25]
[1,] 18000.00 19000.00 20000.00 21000.00 22000.0 23000.00 24000.00 25000.00
[2,] 147.44 156.05 165.46 173.09 184.5 192.92 202.72 212.33
[,26] [,27] [,28] [,29] [,30]
[1,] 26000.00 27000.00 28000.00 29000.00 30000.00
[2,] 220.74 229.74 238.11 248.47 257.23
Dvs om 3 (3.08 i tabellen ovan) personer tillsammans köper 1000 kort får de (i medelvärde) alla får en fullständig serie. På samma sätt om 9 (9.71) personer köper 2000 kort, 17 (17.08) köper 3000 kort så bör de i genomsnitt få fullständiga serier. Osv.
Fokuserar här in på 100 .. 3000 kortinköp:
> sapply(1:30, function(n) rbind(n*100, mean(replicate(100,{ss<-collector.group.sim(100, n*100);min(ss)})) ))
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11]
[1,] 100 200 300 400.00 500.00 600.00 700.00 800.00 900.0 1000.00 1100.00
[2,] 0 0 0 0.13 0.57 1.05 1.48 1.97 2.5 3.17 3.69
[,12] [,13] [,14] [,15] [,16] [,17] [,18] [,19] [,20] [,21]
[1,] 1200.00 1300.00 1400.00 1500.0 1600.0 1700.00 1800.0 1900 2000.00 2100.00
[2,] 4.44 4.99 5.63 6.1 7.3 7.97 8.3 9 9.91 10.41
[,22] [,23] [,24] [,25] [,26] [,27] [,28] [,29] [,30]
[1,] 2200.00 2300.00 2400.00 2500.00 2600.00 2700.00 2800.00 2900.00 3000.00
[2,] 11.17 11.95 12.79 13.53 13.93 15.09 15.85 16.16 17.21
Här ser vi också en-person-problemet: för 600 inköp är det drygt en person som får en full serie, det "exakta" väntevärdet är alltså 519.
Några noteringar
Lite av det vi set ovan:
* Om det är få inköps (säg < 700) får man alltså den 1/10-effekt som både E och jag upplevde i våra respektive barndomar. Det behövs alltså inte någon konspirationsteori för att förklara detta. (Naturligtvis kan detta kombineras med att kort-företaget faktiskt gjorde denna 1/10-tillverkning, men dessa experiment stödjer alltså inte detta.)
* Nätverkets storlek, dvs antalet personer som ingår i det, är inte viktig i denna modell, utan det som är avgörande är hur många kort man tillsammans köper. Det kan vara en person som köper 10000 och de andra 100 stycken, och tillsammans har de alltså 10000+ 10*(N-1) kort vilka sedan kan bytas hur som helst.
Samt en sista notering:
För 519 inköp i ett utbytesnätverk blir det igenomsnitt så här många fullständiga serier:
> table(replicate(1000,{ss<-collector.group.sim(100, 519);min(ss)}))/1000
0 1 2
0.409 0.563 0.028
Vilket är intressant eftersom det i 2.8% av fallen faktiskt skapas 2 stycken fullständiga serier (trist nog befann man sig aldrig i dessa nätverk :). 519 inköpta kort är, som sagt, det magiska medeltalet för att en person skulle få en fullständig serie.
Jämförelse: min/max-analys av svenska Lottodragningar
Här görs en motsvarande min/max-analys av svenska Lottodragningar. I går inhämtades fördelningen av senaste halvårets lottodragningar. (Värdena hämtas från Svenska Spel: klicka på den gröna Lotto-bilden/knappen, och i den uppkomna popuppen klicka på den gröna "Statistik"-knappen.)
Fördelningen av de 35 Lotto-talen är att det minst dragna talet har endast dragits 22 gånger (faktiskt två tal), och det mest dragna talet har dragits 44 gånger. En sorterad fördelning av talen ser ut så här:
> lotto2<-read.table("svensk_lotto2.dat",head=T, sep=",")
> sort(lotto2$dragna)
[1] 22 22 23 24 27 28 28 29 30 30 30 31 31 31 31 32 32 32 32 33 34 35 35 35 35
[26] 36 37 37 38 38 39 40 40 43 44
> sum(lotto2$dragna)
[1] 1144
> min(lotto2$dragna);max(lotto2$dragna)
[1] 22
[1] 44
> min(lotto2$dragna)/max(lotto2$dragna)
[1] 0.5
Det ger alltså ett min/max-förhållande på 22/44 = 0.5. Är det något lurt här? Låt oss ser hur en simulering beter sig. Det är alltså totalt 1144 dragna tal de senaste halvåret och det finns 35 tal, vilket - för att prata i samlarkortproblemets terminologi - motsvarar 35 "kort" och 1144 "inköpta kort"
En exempelkörning:
> sort(ss<-collector.group.sim(35, 1144))
[1] 22 22 22 24 24 26 27 27 28 29 29 29 31 31 32 32 32 33 33 33 33 34 34 35 36
[26] 37 39 39 39 40 41 42 43 43 43
> min(ss)
[1] 22
> max(ss)
[1] 43
> min(ss)/max(ss)
[1] 0.5116279
Medelvärdet för 100 sådana min/max-simuleringar är cirka 0.47, vilket är tillräckligt nära Lotto:s min/max-värde på 0.5 för att vi ska känna oss trygga att Lotto-dragningar inte är påtagligt konstiga.
> mean(replicate(100, {ss<-collector.group.sim(35, 1144);min(ss)/max(ss)}))
[1] 0.466839
Slutkomihåg
I en samling slumpmässiga dragningar som Lotto eller samlarkort är det alltid någon eller några bollar/kort/tal som slumpmässigt dras fler gånger än de övriga, liksom det är alltid någon eller några som dras färre gånger än de övriga.
Man kan förledas att tro att det är något signifikant (speciellt, konstigt, magiskt) med dessa olika extremvärdena, speciellt om det är ett mindre antal dragningar som studerats. Sådana felslut kallas för "The extreme value fallacy" (se nedan).
Se även
Extremvärdesanalys av webbesök, speciellt länken till Number Watch: The extreme value fallacy.
Födelsedagsparadoxen/födelsedagsproblemet: Se t.ex. Sammanträffanden - anteckningar vid läsning av Diaconis och Mosteller 'Methods for Studying Coincidences' (teknisk, men länkar i slutet till andra sidor) samt .
Födelsedagsproblemet kan kanske ses som ett komplement till samlarkortproblemet: I födeledagsproblemet studerar man hur många personer det minst måste vara för att två (eller fler) ska ha samma födelsedag. I samlarkortproblemet är det frågan om hur många personer det måste vara för att alla dagar på ett år ska ha åtminstone en person som har födelsedag på denna person: Enligt det klassiska samlarkortproblemet (för en person som själv samlar kort) är det 365*sum(1/(1:365)) ~ 2365.
En Java-simulering: Coupon Collector Problem, från den trevliga sajten Probability by Surprise.
Posted by hakank at 07:27 EM Posted to Matematik | Sammanträffanden | Statistik/data-analys | Comments (2)
augusti 06, 2005
Lite om konsekutiva talpar i Lotto (och dess varianter)
I Konstantinos Drakakis paper Distances between the winning numbers in Lottery (arXiv, PDF) undersöks sannolikheten för en förekomst av konsekutivt talpar i Lotto-spel. Man ger en formel för denna typ av sannolikhet, och kommer t.ex. fram till att det för ett 6/49-Lotto (dvs där 6 nummer dras av 49) är det ungefär 49.5% chans att en Lotto-rad innehåller åtminstone ett konsekutivt talpar. Vilket är förvånansvärt högt.
Här nedan är några kommentarer och utvikningar, bl.a. med hjälp av riktig data för den Lotto-form vi har i Sverige, 7/35-Lottoformen (dock ej svensk data) samt simulering av sådan Lotto-typ.
Not: Sorterad dragningslista
En not kan vara på sin plats så här i början. Det är frågan om (konsekutiva) talpar i den sorterade listan av de dragna Lotto-numren. Det gäller alltså inte talpar som uppstår i själva dragningen. Exempel: Om en dragning görs av följande "bollar" (1, 14, 34, 2, 19, 15, 20) så tittar vi här på den sorterade listan (1, 2, 14, 15, 19, 20, 34) som ha tre stycken konsekutiva talpar: (1,2), (14,15) samt (19,20).
Notera också att varken Drakakis eller jag här nedan har brytt oss om tilläggstal och andra finesser.
Matematisk formel
Problemet formuleras på följande sätt i papret:
What is the probability that, out of m > 0 numbers drawn uniformly randomly from the range 1,..., n > m, at least two are consecutive?
Dvs vad är sannolikheten att det finns minst ett konsekutivt talpar (dvs ett eller flera) om man drar m tal från intervallet 1..n.
Den slutna matematiska formeln för denna sannolikhet uträknades till
p(n,m) = 1 - p(n,m)= 1 - ( C(n-m+1, m) / C(n,m) )
där C motsvarar (binomialkoefficienten ("n över m") och som i sin tur är definierad som n!/(k!*(n-k)!). Papret visar med matematisk stringens hur man kommit fram till detta resultat, men det vågar jag inte ha någon åsikt om och kommer inte heller att beröra detta här nedan.
Konkret
Låt oss i stället bli konkreta. För den ovan nämnda Lotto-typen 6/49 studerade värdena (n=49, m=6) får man sannolikheten för att det ska finnas minst ett konsekutivt talpar om man drar 6 tal från intervallet 1..47.
I det symboliska matematisk paketet MuPad (fritt att ladda ner och fritt att använda) uttrycks det på följande sätt.
>> n:=49:m:=6:1- binomial(n-m+1,m) / binomial(n,m);float(%);
22483/45402
0.4951984494
dvs det är cirka 49.5% chans att det finns åtminstone ett talpar. Förvånande mycket, eller hur?
Simulering
Min vana trogen har jag även simulerat detta, och lika troget är det gjort i statistikpaketet R. I simuleringen gjordes 100000 "dragningar" - med sample(1:49, 6) - och sedan räknar man hur många tal som ligger intill varandra. (Som vanligt använder jag den kompakta one-liner-formen för denna typ av simuleringar. En liknande simulering har förklarats lite mer ingående här.)
> sum(sapply(1:100000, function(x) {ddd<-diff(xxx<-sort(sample(1:49,6)));sss<-sum(ddd==1);sum(sss>=1)})/100000)
[1] 0.49559
dvs 49.5%, vilket stämmer hyfsat bra med formeln.
Den svenska Lottoforme(l)n: 7/35
OK, denna typ av Lotto kanske inte är så intressant för oss. Vad med den svenska formen 7/35, dvs där man drar 7 nummer av 35? Först tar vi den teoretiska beräkningen (i MuPad):
>> n:=35:m:=7:1- binomial(n-m+1,m) / binomial(n,m);float(%);
8903/11594
0.7678971882
Dvs det är nästan 76.8% chans att det finns åtminstone ett konsekutivt talpar i de svenska lottoraderna. En simulering av 100000 dragningar ger (nästan) samma resultat 76.6%:
> sum(sapply(1:100000, function(x) {ddd<-diff(xxx<-sort(sample(1:35,7)));sss<-sum(ddd==1);sum(sss>=1)})/100000)
[1] 0.76618
Utvidningar av detta
Kommen så här långt funderade jag på några andra saker kring Lottodragningar:
- finns det data för den svenska Lotto-formen?
- hur många konsekutiva talpar finns det i genomsnitt?
- hur är fördelningen för andra typer av talpars-differenser?
Data för Lotto på formen 7/35 (dock ej svensk)
Det vore ju roligt att se hur 7/35 ser ut i praktiken. Finns det då någon lista över en massa dragningar på det detta "svenska" Lotto-format 7/35? Jepp, det finns det. Mattias Hästbacka har samlat resultaten av Lottoraderna på sin Lotto-sida. Den fullständiga listan finns på Lotto-rader från v40/1980 till v17/2005, dvs nästan 25 år.
Observera att detta inte är Svenska Spels Lottodragningar, utan motsvarande "Finska Spel". Men det spelar egentligen ingen roll för det jag vill komma åt.
Om någon har motsvarande dataanhopning för Svenska Spels Lotto så vore jag mycket intresserad av få tillgång till den. (Maila mig gärna i så fall på hakank@bonetmail.com".)
Jag har bearbetat datan och i filen lotto_all_just_numbers.txt finns "rena" rader utan någon annan information, förutom en tillbörlig källhänvisning till Mattias Hästbackas sajt.
Analys av data
OK, tillbaka till undersökningen. Det finns i Mattias Hästbackas datamängd 957 rader med åtminstone ett konsekutivt talpar av 1283 dragningar, vilket är 957/1283 = 0.746, dvs 74.6%.
Det teoretiska värdet är som vi såg ovan 76.8%, vilket skulle motsvara 1293 * 0.7678971882, dvs ungefär 985 rader. Skillnanden mellan det praktiska värdet (957) och det teoretiska (985) är 985 - 957 = 28, vilket är ett fel på 28/1283, dvs ungefär 2.2% , vilket väl får anses vara rätt hyfsat.
Hur många par blir det i genomsnitt?
Den andra frågan är något annorlunda än Drakakis ursprungliga. Hans utgångspunkt var hur stor sannolikheten är för att det ska bli ett eller flera konsekutiva talpar (dvs åtminstone ett) i en dragning. En annan fråga man kan ställa sig är: hur många konsekutiva talpar det i genomsnitt blir per dragning.
Här är den första dragningen som Mattias Hästbacka sparade (vecka 40 1980):
7, 8, 9, 16, 17, 18, 30
Det finns alltså fyra konsekutiva talpar (7,8), (8, 9), (16, 17) samt (17, 18). Så, frågan är då hur många sådana talpar det blir i genomsnitti per dragning.
En körning på Hästbackas data ger totalt 1429 konsekutiva talpar och på 1283 dragningar blir det 1429/1283 = 1.113796. Dvs för varje dragning blev det igenomsnitt 1.1 konsekutivt talbar.
Äpplen och päron
Men, kan man nu fråga sig, hur rimmar detta 1.2 talpar per dragning med att det finns 76.6% chans för att det blir åtminstone ett konsekutivt talpar per dragning? Borde sannolikheten inte bli 100% istället? Nej, det är två olika saker (olika äpplen och päron).
Konstantinos formel tar inte hänsyn hur många konsekutiva talpar det är utan endast om det är ett eller fler. Dvs det spelade ingen roll för honom om det är 1 sådant par eller 4. Denna senare uträkning tar däremot hänsyn till detta antal. Den andra skillnaden (päronet alltså) är att vi inte räknar med sannolikheter längre utan med det genomsnittliga antalet per dragning.
Fördelning av konsekutiva talpar
En fördelning av antalet konsekutiva talpar i Hästbacka-datan är
0: 325 (0.25)
1: 565 (0.44)
2: 318 (0.25)
3: 69 (0.05)
4: 4 (0.00)
5: 1 (0.00)
Dvs det finns 325 Lotto-rader utan något konsekutivt talpar (cirka 25% av alla dragningar), 565 rader med exakt 1 konsekutivt talpar (~44%) och en rad med 5 par, nämligen den 581:e dragningen (vecka 47 år 1991) som gav följande tal 15 32 33 34 35 36 37.
Låt oss nu för skoj skull simulera detta. Koden som används ser ut så här:
num.talpar = function(num.sims=1283, n=35, m=7) {
# initiera tabellen som kommer att innehåla antalet
# konsekutiva talpar. Det kan vara max m-1 (här 7-1=6) sådana talpar,
# men vi måste även ha med 0, vilket innebär att det blir m stycken
konsek.talpar = rep(0, m)
for (i in 1:num.sims) {
ss = sort(sample(1:n, m))
dd = diff(ss) # differensen mellan talen
tt = sum(dd==1) # hur många konsekutiva talpar finns det
# öka med 1. Not: "tt+1" är för att även få med dragninar som
# inte har något konsekutivt talpar
konsek.talpar[tt+1] = konsek.talpar[tt+1] + 1
}
return(konsek.talpar)
}
Här är en sådan körning som har värden som inte är helt olika de faktiska (dvs Hästbacka-datan). Först antal och sedan fördelningen.
> (ss = num.talpar(1283))
[1] 314 519 353 88 8 0
> round(ss/1283,2)
[1] 0.24 0.40 0.28 0.07 0.01 0.00
För just denna simulering blev det alltså cirka 314 dragningar (cirka 24%, av 1283 rader) utan något konsekutivt talpar alls, 519 dragningar med ett sådant talbar, och hela 8 dragningar med 5 k.t.p (dvs där det finns 6 konsekutiva tal).
Om vi nu brassar på med 100 sådana här simuleringar om vardera 1283 dragningar, dvs 1283*100 = 128300 dragningar (och delar de värden vi får med 100) så får vi något mer exakta värden att jämföra med:
> (ss=num.talpar(1283*100)/100)
[1] 299.31 540.63 339.48 92.53 10.60 0.45 0.00
> round(ss/1283,2)
[1] 0.23 0.42 0.26 0.07 0.01 0.00 0.00
Vi ser alltså att det finns cirka 23% chans att det blir 0 stycken k.t.p., cirka 42% att det blir exakt ett k.t.p. osv.
Den intressanta frågan blir då vad är det (simulerade) genomsnittet konkekutiva par per dragning. I faktisk data blev det cirka 1.1 konsekutivt par per dragning.
sum.talpar = function(num.sims=1283, n=35, m=7) {
antal.talpar = 0
for (i in 1:num.sims) {
ss = sort(sample(1:n, m))
dd = diff(ss) # differensen mellan talen
tt = sum(dd==1) # hur många konsekutiva talpar finns det
antal.talpar = antal.talpar + tt
}
return(antal.talpar)
}
sum.talpar()
Först en enkel körning för att få en känsla för informationen.
> ss = sum.talpar(1283)
[1] 1580
> ss/1283
[1] 1.231489
Och sedan en lite tyngre körning
> sum.talpar(1283*100)/(1283*100)
[1] 1.200514
Dvs det blir cirka 1.2 konsekutiva talpar per dragning. Det är alltså mer än ett par i genomsnitt.
Hur fördelas differenserna av talen?
Ovan har vi endast studerat konsekutiva talpar, dvs tal där differensen är 1. Nen det är även intressant att studera övriga differenser som uppkommit i dragningarna. Det vi ovan kallat för "konsekutiva talpar" är talpar med differensen 1, vilket vi i det följande kallar "1-differens".
I Hästbacka-datan fördelas sig differenserna enligt följande (på formatet differens: antal förekomster). Notera att en dragning nästan alltid har flera olika differenser. T.ex. ovanstående 5-talpars-dragning (15 32 33 34 35 36 37) har fem stycken 1-differenser samt en 17-differens (dvs 32 - 15 = 17).
1: 1429
2: 1184
3: 939
4: 790
5: 683
6: 585
7: 447
8: 345
9: 283
10: 231
11: 207
12: 126
13: 108
14: 99
15: 66
16: 48
17: 44
18: 17
19: 22
20: 11
21: 16
22: 2
23: 5
24: 2
25: 3
Man kan här se att det är flest 1-differenser, sedan blir det ständigt färre och färre.
OK, för fullständighets skull så simulerar vi även detta. Koden är rätt lik den föregående.
diff.table.sim = function(num.sims=1283, n=35, m=7) {
diff.table = rep(0, n)
for (i in 1:num.sims) {
ss = sort(sample(1:n, m))
dd = diff(ss) # differensen mellan talen
# lägg in respektive differens i tabellen
for (d in dd) {
diff.table[d] = diff.table[d] + 1
}
}
return(diff.table)
}
Det vi söker är alltså det genomsnittliga antalet differens per dragning, så vi simulerar 100000 dragningar.
> cbind(diff.table.sim(100000)/100000)
[,1]
[1,] 1.19969
[2,] 0.98629
[3,] 0.80547
[4,] 0.65678
[5,] 0.52912
[6,] 0.42424
[7,] 0.33684
[8,] 0.26439
[9,] 0.20978
[10,] 0.15981
[11,] 0.12235
[12,] 0.09001
[13,] 0.06614
[14,] 0.04662
[15,] 0.03512
[16,] 0.02358
[17,] 0.01583
[18,] 0.01097
[19,] 0.00734
[20,] 0.00406
[21,] 0.00281
[22,] 0.00149
[23,] 0.00073
[24,] 0.00033
[25,] 0.00013
[26,] 0.00006
[27,] 0.00002
[28,] 0.00000
[29,] 0.00000
[30,] 0.00000
[31,] 0.00000
[32,] 0.00000
[33,] 0.00000
[34,] 0.00000
[35,] 0.00000
Varvid vi kan se att det är i genomsnitt (nästan) 1.2 stycken 1-differenser (dvs det vi ovan kallade konsekutiva talpar) per dragning, i genomsnitt 0.99 2-differens per rad osv.
Genomsnittlig antal differenser
Det genomsnittliga antalet differenser är cirka 4.53 enligt följande simulering. Här delas summan av differensvärdena med det totala antalet uppkomna differenser. (Man kan trixa med föregående värden, men jag vill ha lite kontroll över saker och ting.)
diffs = function(num.sims=1283, n=35, m=7) {
diffs = 0
num.diffs = 0
for (i in 1:num.sims) {
ss = sort(sample(1:n, m))
dd = diff(ss)
for (d in dd) {
diffs = diffs + d
num.diffs = num.diffs + 1
}
}
m = diffs/num.diffs # genomsnittligt antal
return(c(diffs, num.diffs, m))
}
Och så körningen, där vi endast är intresserade av det sista värdet:
> round(diffs(1283*100),3)
[1] 3465204.000 769800.000 4.501
Vilket alltså ger det genomsnittliga differensvärdet 4.501. Äh, vi säger 4.5.
Sammanfattning
Här ovan har vi kommit fram till bl.a. följande:
* Sannolikheten att det ska förekomma åtminstone ett konsekutivt talpar i en 7/35-dragning är cirka 77%
* Det blir i genomsnitt 1.2 konsekutiva talpar per dragning.
* Det genomsnittliga differensvärdet för en dragning är 4.5.
Som antytts så anser i alla fall jag att det är förvånande.
Upprinnelse (inspiration)
Upprinnelsen till allt detta var notisen Consecutive pairs in winning lottery numbers hos MathForge.
Se även
Se även min genomgång av födelseparadoxen,tillika med R-kod, i Sammanträffanden - anteckningar vid läsning av Diaconis och Mosteller 'Methods for Studying Coincidences'.
Jämför även med den simulering som gjordes för ett liknande problem (6/49-Lotto) i Lite om resampling, simulering, sannolikhetsproblem etc.. Sök efter "Litet problem i (engelsk) Lotto". (Det koms dock inte fram till exakt samma sak.)
Samt överhuvudtaget Simulation, probability theory etc, såsom Trisssimuleringen (Java applet).
Posted by hakank at 03:37 EM Posted to Matematik | Statistik/data-analys | Comments (8)
juli 23, 2005
Annals of Improbable Research: Namntal (Name Number) för en profession
Även om jag just nu inte kan ge några bra exempel så är det inte helt sällan jag ser t.ex. i TV-intervjuer, eftertexter till filmer eller ute i allmänna livet, efternamn som får mig att fundera kring kopplingen mellan efternamn och yrke/profession/intressen. T.ex. en elektriker som heter Ström får väl en att börja undra, liksom en murare som heter Tegel.
I den excellenta tidskriften för otroliga forskningsresultat Annals of Improbable Research (AIR, Improbable Research är kanske mest kända för sitt Ig Nobel Prize) finns det att beläsa om s.k. Name Numbers (här nedan namnat "namntal") för en forskningsgren. Ett sådant namntal anger andelen personer inom en forskningsgren som har ett efternamn kopplat till denna forskningsgren.
Ursprungsartikeln för denna forskning skrevs av Kevin Krajik och var kring geologi i The "Name Number" for Geology, and for Other Professions, Annals of Improbable Research, vol. 11, no. 2, March/April 2005 (tyvärr ej funnen å lina och därför inte läst, men borde finnas här).
Den visade att namntalet för geologi är 1.35% (dvs att 1.35% av de som forskar inom geologi har namn som är kopplat till geologin). Emedan jag inte läst originalstudien får hänvisas till sekundär källa kring dess urval (från Astronomistudien, se referens nedan, och det är min alldeles egenhändigt befetade befetning):
Krajick calculated the Name Number for geology by dividing the number of geology-related surnames for those who presented papers at the 2003 meeting of the Geological Society of America by the total number of authorial surnames for that meeting. The geology Name Number presented in Krajick's study was 117 / 8639, or 0.0135432.
Namntalet för astronomi är 0.0027143 (0.27%), dvs betydligt lägre. Detta enligt Eric Schulman och Caroline V. Cox: The Name Number for Astronomy. Namntalsnamn här är Sun, Moon, Starr etc.
Det har även gjort en liknande studie kring statvetenskap, Richard Neimi (misspelled) The Name Number(s) for Political Science (PDF) som
... examined the 4,529 names (including those occurring more than once) appearing in the on-line index to the program for the 2005 national conference of the Midwest Political Science Association.
Författaren beskriver sedan flera namntalsvärden. Det första resultatet är 1.26% (vilket alltså är lägre än geologernas). Exempel på sådana namn: King, Prince, Good.
Sedan gör dock författaren en, enligt min mening, något farlig abrovink och antar att efternamn på amerikanska presidenter och andra statsmän är giltiga namntalskopplingar och kommer således upp i hela 2.08%. (Detta är - som metod betraktad - en farlig metod eftersom det räcker med att en eller ett fåtal presidenter har väldigt vanliga namn för att namntalet ska öka drastiskt och orättvist. Såvida man inte tillåter detta inom andra professioner också, t.ex. att fysiker som heter Newton, Pascal etc är namntalsnamn. Hmmm, dessa båda är faktiskt fysiska konstanter och borde vara namntalsnamn bara av det skälet. OK, vad med de som studerar filosofi och har samma namn som kända filosofer t.ex. Wittgenstein, Sarte och Marx? Nej, jag tycker inte att det borde vara tillåtet med endast efternamnkopplingar. Eller i alla fall att de i så fall indexeras på ett speciellt sätt såsom att räknas med en faktor f, t.ex. 1/3, eller sätts i en speciell kolumn till höger om de "riktiga" kopplingarna.)
Däremot gör författaren sedan några intressanta uppföljningsstudiefrågor vilket gör att man gärna och snart förlåter dennes abrovinklande:
Further study could look into the sub-specialties of the above-mentioned authors. Do Professors Washington, Adams, and so on study the presidency? Or at least American politics? Are Gandhi and Mao Indian and Chinese specialists, respectively? Do Wiseman, Goodman, Fair and Bliss study political philosophy? Do Power, Powers, and Guerra write about International Relations? From there, one could move on to consider whether persons take on any of the characteristics of the leaders (or kinds of leaders) whose names they bear. Are Law and Lawless opposites? Is Fair fair? And what should we expect from the Nixons? And, of course, one could see whether names and particular kinds of colleges and universities are linked. Are the Popes at Catholic institutions? Does Canon’s school have an ROTC program? These and many other fascinating questions await more detailed analyses.
Vänligen bemärk att AIR har en blogg: Improbable Research What's New -- News about research that first makes people LAUGH, and then makes them THINK. This is the official blog of the Ig Nobel Prizes and of the Annals of Improbable Research (AIR).
(Parentes 1: Det mesta ovan via just denna blogg, mer specifikt blogganteckningen Name number for political scientists.)
Slutfråga
För att avsluta med en slutfråga: När kommer den första svenska tillämpningen av denna nya forskningsgren? Och man skulle också kunna undra vilken typ av efternamn som ger namntalspoäng inom området.
En ännu sistare sak: Mitt efternamn, Kjellerstrand, har inga tydliga beståndsdelar som ger namntalspoäng i någon forskningsområde alls, vilket kanske skulle förklara en del eller annat. Några möjliga men åletade kopplingar: "Kjell" skulle kunna vara "källa" och kanske kunna kopplas till filosofi (sökande efter källan till vis(s)het) eller till vatten (jag dricker rätt mycket te), och "strand" kopplas till sand som vidare kopplas till att smula sönder saker (t.ex. namn) till dess minsta beståndsdelar, såsom just denna analys. Eller helt enkelt att jag är en lat person som tycker om att sitta vid en strand (läs: på balkongen eller i en park) och läsa en bok.
(Parentes 2: Den mer eller mindre vanligtvis observante läsaren kanske observerar kategoriseringen av denna anteckning till Sammanträffanden. Och det är ingen slump.)
Posted by hakank at 08:58 FM Posted to Sammanträffanden | Statistik/data-analys
juni 28, 2005
InfoVis: The Landscape Metaphor
InfoVis: The Landscape Metaphor beskriver datavisualiseringar med hjälp av landskapmetaforen.
Whoever that has followed a driving course is able to catch the meaning of a traffic signal in a fraction of a second. Nevertheless if we show the same signal to someone that hasn't been taught how to interpret it or has never seen one, it will be very difficult for him or her to get the meaning in its complete magnitude, even if staring for a long time in front of it trying to decipher it ... In the end, it seems that decoding a map, be it spatial or thematic, results quite natural for most of the human beings, requiring just very little training. This doesn't appear to be the case with more recent developments of more abstract nature, like parallel coordinates or hyperbolic geometry, just to mention a couple of examples. ... The landscape metaphor, and spatialisations in general, constitute very attractive ways of representing big amounts of data in an intuitive way. The notions of distance and height are easily understood by many people, even when they encode other variables like similarity, density, or prevalence of a certain term.
En av de tekniker som beskrivs är Islands of Music (Matlab-kod finns att tillgå):
Islands of Music are a graphical user interface to music collections based on a metaphor of geographic maps. Islands represent musical genres. Mountains and hills on these islands represent sub-genres. The islands are situated in such a way that similar genres are close together and might even be connected by a land passage while perceptually very different genres are separated by deep sea. The pieces of music from the collection are placed on the map according to their genre. To support navigation on the map the mountains and hills are labeled with words which describe rhythmic and other properties of the genres they represent.
Posted by hakank at 11:07 EM Posted to Statistik/data-analys
juni 13, 2005
Ivars Peterson: En matematisk analys av tennis
Ivars Peterson skriver i MathTrek : Winning at Tennis om matematisk och statistisk analys av tennis:
In the April Studies in Applied Mathematics, Paul K. Newton of the University of Southern California and Joseph B. Keller of Stanford University provide formulas for computing a tennis player's chances of winning and, in effect, for predicting the outcome of tennis tournaments. In the context of their model, Newton and Keller also prove that the probability of winning a set or match doesn't depend on which player serves first.It isn't enough to know just the rankings of the two players in a tennis match. There's no obvious, unambiguous way to translate a ranking into a probability of winning. Instead, it turns out that the key factor is the probability that each player wins a rally against the other player when he or she serves. Typically, you assume that these probabilities stay the same throughout a match.
Referenser till gjord forskning finns i artikeln, vilken se. Tyvärr är många artiklar inte publikt tillgängliga.
Se även Ivars Petersons tidigare MathTrek
Posted by hakank at 07:55 EM Posted to Matematik | Sport, idrott, hälsa | Statistik/data-analys | Comments (1)
juni 06, 2005
John Allen Paulos: What Numbers Reveal -- from Sumo Wrestlers to Professors
Inte helt förvånande skriver John Allen Paulos om boken Freakonomics: What Numbers Reveal -- from Sumo Wrestlers to Professors:
Looking at large data sets and deriving loud conclusions from the reams of whispering numbers is often enjoyable. Herein are three quite disparate examples.
The first concerns Sumo wrestlers and comes from Freakonomics, a fascinating new book by economist Steven Levitt and writer Stephen Dubner, that employs Levitt's quirky economic insights to illuminate many everyday activities and practices. The second is simply a study I reported on in a book I wrote on the stock market, and the third comes from a simple analysis I recently made of grade distributions for a required math course at my university.
Se även
Tidigare anteckningar (google) om Paulos
Recension av boken Freakonomics Steven D. Levitt, Stephen J. Dubner: Freakonomics : A Rogue Economist Explores the Hidden Side of Everything
Posted by hakank at 12:56 EM Posted to Matematik | Statistik/data-analys
maj 15, 2005
Mats Anderssons veckodagsundersökning: Kommentar samt komplettering
I Vad har världen emot tisdagar? tar Mats Andersson åter upp sin fascinerande veckodagsnamnssökning.
Mitt rätt långa svar från i går på hans blogg följer nedan, justerat med länkar, pronomenjusteringar, punktomflyttning och aktuella sökresultat. Detta är dock inget försök att hijacka diskussionen från Mats, så gör eventuella kommentarer hos hos Mats.
Det har hänt saker i siffrorna sedan gårdagen, så de har lagts till (med "Idag:"). Om inte annat så lär detta oss att tillvaron fluktuerar ("man får inte samma sökresultat två dagar i rad"). Se även google som bevis.
3. Både [Mats] och jag har skrivit om detta tidigare. Här är min - vad jag tror då trodde - sista anteckning med länkar tillbaka till våra tidigare anteckningar: Veckodagsnamn på google - återkomsten
1. [Mats] har gjort en universell sökning (egentligen jordisk), men det - och det är här jag framhärdar - bör vara "sökningar på svenska" vid googlingen. Se t.ex. diskussionerna kring en av [hans] tidigare anteckningar (något senare än den [han] länkar till i den aktuella anteckningen).
T.ex. är "Måndag Oy" ett finskt namn. "å":et översätts också till "aa" där det blir en del utomsvenskliga träffar; Fredag är ett namn på en romanfigur etc.
2. Jag gjorde därför om sökningen på google med "sidor på svenska" och fick följande:
Måndag 758000 (3) Idag: 750000 (7)
Tisdag 687000 (4) Idag: 779000 (6)
Onsdag 626000 (7) Idag: 785000 (5)
Torsdag 680000 (5) Idag: 790000 (4)
Fredag 1060000 (1) Idag: 1190000 (1)
Lördag 928000 (2) Idag: 1120000 (2)
Söndag 673000 (6) Idag: 798000 (3)
Siffrorna inom parentes anger rankningen, fredag och lördag ligger alltså bäst till. (Idag: rankningen har förändrats kraftigt förutom för fredag och lördag)
Här ligger tisdag inte så pjåkigt till (Idag: jo, det gör den), vilket däremot onsdag gör. Det går tyvärr inte att jämföra mina äpplen (sökningar på svenska) med [Mats] päron (på alla språk), så vi kan inte direkt siffersätta förändringen...
3. [Flyttades upp.]
4. Diskuterade vi inte tidigare att det kanske finns mer "lördag" och "söndag" eftersom det är helg och bl.a. bloggare skriver fler anteckningar då? Detta är testbar hypotes. Här genom att söka på "blogg" samt veckodagsnamnet (vilket iofs kan kritiseras om det är en bra indikation):
blogg måndag 10100 (3) Idag: 31700! (1)
blogg tisdag 7980 (6) Idag: 7870 (7)
blogg onsdag 8930 (4) Idag: 29000! (2)
blogg torsdag 7550 (7) Idag: 22900! (3)
blogg fredag 13400 (1) Idag: 11900 (4)
blogg lördag 11800 (2) Idag: 11900 (4)
blogg söndag 8370 (5) Idag: 8350 (6)
Här [var det igår] i stort sett samma rankning som ovan, men idag (söndag) ligger tisdag mest pyrt till. Märkligt nog ligger söndag rätt dåligt till, och det stödjer inte helghypotesen.
Man kan f.ö. notera att bloggare står för drygt en procent av dagsnamnen och det skiljer sig inte märkbart över veckodagarna: alla ligger kring 1.3 procent. Här är mer exakta värdena (sökresultatet för "blogg veckodag" delat med antalet sökresultat för "veckodag", där "veckodag" är veckodagesnamnet).
Måndag: 0.013 (Idag: 0.042 !)
Tisdag: 0.012 (Idag: 0.010)
Onsdag: 0.014 (Idag: 0.037 !)
Torsdag: 0.011 (Idag: 0.029 !)
Fredag: 0.013 (Idag: 0.010)
Lördag: 0.013 (Idag: 0.011)
Söndag: 0.012 (Idag: 0.010)
Idag: Här står måndag, onsdag och torsdag ut ordentligt, vilket ännu mindre stöder "helghypotesen".
5. Jag tror att det finns en hel del slump och annan google-galenskap med i spelet.
Posted by hakank at 07:38 EM Posted to Språk | Statistik/data-analys | Sökmotorer | Comments (1)
maj 13, 2005
Chance News Wiki: ChanceWiki
Chance News är en underbar och fritt tillgänglig källa kring statistik som ofta tar upp innumeracy ("innumerati", "sifferblindhet" eller vad det svenska ordet är för vår okunskap eller dåliga intuition kring siffror) i olika former. Sajten presenterades mer i Chance News (och sajt).
Nyhetsbladet har nu blivit en Wiki för att få mer interaktivitet med och aktivitet hos läsarna: ChanceWiki. Första Wiki-numret finns här Chance News (April-May 2005. Se även Arkivet (icke-wikifierat).
Andra sajter:
Sajten innumeracy.com
John Allen Paulos fantastiska bok Innumeracy: Mathematical Illiteracy and Its Consequences (Bokus, ISBN: 0809058405).
Posted by hakank at 08:55 EM Posted to Statistik/data-analys
maj 11, 2005
"The Long Tail" och "long tail"
Chris Anderson, som myntade den marknadsmässiga/kulturella termen "The Long Tail" (i bestämd form), redogör på sin blogg The Long Tail om upprinnelsen till termskapandet och jämför med det äldre statistiska begreppet "long tail". Det gör han i The origin of "The Long Tail":
To be precise, what I coined was the notion of looking at the tail itself as a new market. The use of the proper noun (including "The") is not incidental, but is intrinsic to the observation that we have historically looked at the market at the head of the curve in isolation, and we can now shift our gaze to the right and see that the tail is another market.
(Mycket "Long Tail" blev det visst...)
Relaterat
Wikipedia-artikeln The Long Tail.
Stefan Waldeck skriver bl.a. om dessa saker på sin blogg State808 (State808 is about the Internet, Digital Media and Marketing.). Se t.ex. anteckningen Search Long Tail. (Ny-bloggtipset kom via Henrik Torstensson.)
Posted by hakank at 05:51 EM Posted to Spelteori och ekonomi | Statistik/data-analys
maj 08, 2005
Sällskapsspel, strategier och spelteori
BBC News-artikeln Scissors, paper, stone - a strategic game beskrivs inledningsvis en lite märklig historia där två auktionsfirmor tävlade om en kunds kontrakt genom att spela sten-sax-och-påse.
You probably thought scissors, paper, stone was a game of chance not strategy. But you'd be wrong. Christie's auction house won a £10.5m contract by playing the game tactically - so is there more to such games than meets the eye?
En intressant sak här är vilka experter som (vinnaren) Christie hade frågat. Har ett storföretag verkligen inte har någon annan expert att fråga (eller så är det en frisering för att söta till en historia).
...but Christie's asked the experts, Flora and Alice, 11-year-old daughters of the company's director of Impressionist and modern art, and aficionados of the game.
They explained their strategy:
1. Stone is the one that "feels" the strongest
2. Therefore a novice will expect their opponent to go for stone, and will go for paper to beat stone
3. Therefore go for scissors first
Sure enough, the novices at Sotheby's went for paper, and Christie's scissors got them an enormously lucrative cut.
Derren Brown har i sina shower visat stor förmåga att förutse/påverka sina motståndare i detta spel och använder troligen en något mer avancerad variant än ovanstående. Varför frågade de inte honom?
Sedan nämns översiktligt studier om strategier för olika spel (där man felstavat några namn). Här är några nedslag till referenser:
* Rock, Paper, Scissors (Sten, sax och påse)
Se wikipediaartikeln Rock, Paper, Scissors.
Några introduktioner kring spelteori som nämner spelet:
A Brief Introduction to Game Theory
Games, Dilemmas, and Traps
* Monopoly
(den engelskspråkiga varianten av Monopol).
Troligen är det Neil Thompson (inte Thomson) man avser i artikeln, i alla fall har en sådan skrivit Monopoly Statistics and Strategy som innehåller strategier och statistik för spelet.
Två andra sajter:
Durango Bill's Monopoly Probabilities.
Truman Collings har skrivit om sannolikheterna för det amerikanska Monopoly: Probabilities in the Game of Monopoly (som också innehåller ett C-program för simuleringen).
(Colling har gjort andra roliga saker, t.ex. både en solver och en generator för alphametics-problem, dvs problem såsom SEND + MORE + MONEY, där man ska ersätta bokstäverna med siffror så att additionen blir korrekt.)
* Connect Four
Han som skrev sin doktorsavhandling om Connect Four heter Victor Allis (inte Allen): A Knowledge-based Approach of Connect-Four The Game is Solved: White Wins (CiteSeer).
Fler referenser om spelet finns hos MathWorld Connect-Four.
* Samlingssajter
Slutligen två sajter som har helt olika inriktningar:
Combinatorial Game Theory är en länksamling för matematisk forskning om bl.a. sällskapsspel.
En annan intressant sajt och som jag ofta besökte för några år sedan är Machine Learning in Games. index of games har en listning över de olika spelen. Sajten har dock inte uppdaterats sedan 2002.
Posted by hakank at 08:45 FM Posted to Machine learning/data mining | Spelteori och ekonomi | Statistik/data-analys
maj 04, 2005
Estimering av antalet trogna besökare på en blogg: En skiss
Av lite olika skäl (mestadels förflugna kommentarer via mail) har jag försökt att komma på en modell för hur många trogna läsare det finns på min blogg (och mer generellt på bloggar överhuvudtaget), dvs läsare som läser den regelbundet och inte "bara" råkar komma in på den av misstag via sökmotorer eller länkar.
Jag vill inte använda webbstatistiken av skäl som beskrivs nedan, utan försöker komma fram till en annan modell.
Vad är en "trogen läsare"?
Egentligen vill jag inte göra en formell definition av detta begrepp, men enkelt kan man väl säga att en trogen läsare är en som återkommande läser eller åtminstone skummar igenom allting som skrivs på bloggen. En prenumerant på en papperstidning är en trogen läsare om denne åtminstone bläddrar igenom tidningen dagligen och läser mer noga här och där.
Man kan notera att jag här nedan försöker att skapa en operationell (mätbar) definition av en trogna läsare. Sådana kan vara mer eller mindre intuitionsvidriga, ju mindre desto bättre.
Har ni - mina mer eller mindre trogna läsare - några bättre intuitioner?
Antal läsare via RSS-system och liknande
Fler och fler läser bloggar via RSS-system. Själv använder jag bloglines och läser oftast samtliga blogganteckningen via detta system och går alltså rätt sällan till bloggen. Detta utgör ett mörkertal om man endast studerar webbstatistiken, och det är anledningen till att jag inte vill använda denna typ av statistik för analysen.
Ett rimligt antagande är att om någon prenumererar via RSS-system så är det en trogen läsare.
Här är prenumerationstalen för RSS-bevakare och andra för min egen blogg:
* bloglines-prenumerationer: Det finns just nu 29 + 41 + 4 (minus mina egna 3 självbevakningar) = 71 prenumeranter. Det är säkert många som inte använder systemet längre. Om vi antar att 30 har slutat med bloglines, innebär det 71 - 30 = 41 läsare.
* cirka 20 via andra RSS-läsare. Jag har här försökt ta bort de som klart är inte är privatpersoner (t.ex. bloglines).
* ett 10-tal via nyligen.se / intressant.se . Jag gör nu ett antagande att flera av besökarna härifrån är trogna.
Det skulle innebära att det finns cirka 40 + 20 + 10 = 70 trogna läsare. Det låter ju trevligt!
Antal kommentarer
Ett annat sätt att se detta, och för att göra en rimlighetsbedömning om antalet, är att studera antalet som skrivit kommentarer, och sedan försöker att arbeta baklänges för att lista ut hur många av dessa som är trogna läsare, och även att jämföra med ovanstående estimering.
Totalt antalet kommentarer från juni 2003 är 1499, varav jag själv är orsak till 597 av dem (dvs cirka 40%). Antalet personer som kommenterat här någon gång här är 214. (Oj, är det så många?)
Men många av kommentatarerna har varit frågor efter gmail-konton och kommit hit via sökmotorer och kan därför inte räknas till de trogna. Så jag har valt att endast räkna med antalet personer som kommenterat 2 eller fler gånger, vilket för tillfället är 83. (Det innebär att det är 214-83 = 131 "enpinnare".)
Men det är inte rimligt att alla (mer än alla eftersom 83 trogna kommentatorer / 70 trogna läsare enligt beräkningarna ovan ~ 1.18!) som läser bloggen kommenterar den, så något är konstigt. I stället vore det väl rimligare att - säg - var 6:e läsare kommenterar. Detta skulle innebära att det är 83 * 6 = 498 mer eller mindre trogna läsare.
Vilket i sin tur innebär att cirka halva den svenska bloggosfären skulle läsa denna blogg, vilket inte heller låter rimligt. (Antalet i den svenska bloggosfären definierat som antal som pingar eller pingat nyligen.se: för närvarande 1124 stycken, även om en del av dessa inte är aktiva längre).
Man kan här jämföra med bloggare som har betydligt fler Bloglinesprenumeranter än jag, säg Erik Stattin med sina åtminstone 140+ prenumerationer, vilket i denna modell skulle ge åtminstone 140 * 6 = 840 trogna läsare, något som jag i och för sig tycker verkar fullt rimligt.
Men: Antalet kommentarer är från dag 1 i bloggens liv (alltså juni 2003). Alla tidigare trogna läsare är säkert inte trogna läsare längre. Då skulle man kunna tänka sig följande: Över en period på här nästan två år är det stor chans att nästan alla trogna läsare har kommenterat 2 eller flera gånger. Vilket gör att 1 på 6 är alldeles för optimistiskt som estimat. I stället kanske det skulle vara 1 på 2, dvs att varannan trogen läsare kommenterar. Detta skulle innebära 83 * 2 = 166 trogna läsare, eller snarare: 166 personer som är eller har varit en trogen besökare.
Detta tangerar den fråga som jag ville undvika: Vad är egentligen en trogen besökare? (En person som säger upp sin tidningsprenumeration är inte trogen längre.) Svaret på den frågan får nog anstå till en annan gång.
Icke-bloggande trogna läsare
Nu bör man komma ihåg att det är fler än de med egna bloggar som läser bloggarna och som kan vara trogna läsare. Frågan är hur många. Jag försökte ge mig på en liknande modell häromveckan i Internetworlds bloggomröstning. Tack, ni 8!, men lyckades inte så bra. Och gör inget nytt försök nu heller.
Min egen erfarenhet är att flera av de tidigare icke-bloggande trogna läsarna sedan har själv startat en blogg, eller håller på att göra det, så detta värde är nog komplicerat att beräkna.
Det förblir sålunda fortfarande ett mörkertal.
Lite mer om antal kommentarer per besökare
När det gäller antal kommentarer per besökare skiljer det sig säkerligen mellan olika bloggar beroende på olika faktorer. Här är några tänkbara sådana:
* vilket typ av blogg det är, t.ex. vilka ämnen som behandlas. En fackblogg har kanske färre besökare men kanske fler av dem kommenterar? Mer allmänna ämnen eller mer allmänt hållna ämnen tenderar nog att skapa fler kommentarer.
* den allmänna stilen/attityden på bloggen, t.ex. om det är "inbjudande" att kommentera.
* vilket typ av bloggare det är, t.ex. hur ofta eller hur bra denne
bemöter kommentarer hos sig. Om denne inte svarar på kommentarer (via kommentarer eller i blogganteckning) tenderar nog många besökare att tröttna på att kommentera efter hand. Man kan också fråga sig om denna faktor även påverkar antalet trogna besökare.
* kanske även språket: en engelskspråkig blogg har nog både fler trogna läsare och fler som kommenterar genom att de når ut till en större målgrupp. Frågan är om engelskspråkiga bloggar genererar ett bättre kommentar/besökare-förhållande än svenska? Finns det något i kynnet hos svenska bloggbesökare som skulle göra att vi tenderar att kommentera mindre eller mer?
* eventuellt även hur mycket bloggaren kommenterar hos och länkar till andra bloggare. Det har påpekats flera gånger att bloggosfären är ett enda ryggdunkande och det ligger lite i det. Kommentarer är ett utmärkt sätt att dunka ryggar: om du kommenterar hos (eller länkar till) mig så kommenterar jag hos dig. Detta är troligen en stor drivkraft till bloggandet eftersom man på detta sätt bygger upp sitt nätverk av kontakter, och större nätverk är oftast bra.
Det skulle vara roligt att sätta någon form av vikt till dessa faktorer, men det är väl hart när omöjligt. Ännu, ska man nog tillägga; någon kanske skapar fina modeller om detta så småningom.
Posted by hakank at 11:36 EM Posted to Blogging | Statistik/data-analys | Comments (9)
maj 01, 2005
The long tail of programming languages
Charles Simonyis (Intentional Software) skriver i The long tail of programming languages om att användningen av programspråk förhåller sig till varandra som en long tail (cf power laws). Man har använt statistiken från TIOBE Programming Community Index for April 2005 (se kommentar nedan).
Vilka slutsatser drar man så av denna långa svans?
* Generella programspråk tenderar av användas mest eftersom de är generella (vilket ju verkar rimligt)
* Det finns språk som ofta är bättre än generella att lösa problem i en specifik domän (nischen), t.ex. Prolog för logikprogrammering.
* Det är svårt för nya programspråk att lyckas slå igenom ordentligt eftersom det krävs bra miljöer för professionell utveckling.
Här är några reflexioner angående detta.
Förutom dessa mer rationella skäl finns det andra saker som gör att användningen fluktuerar. T.ex. Ruby:s Ruby on rails har gjort att fler har fått upp ögonen för Ruby; Pugs som är en trevlig Perl 6-implementation skriven i Haskell - som redan efter några månaders utveckling fungerar förvånansvärt bra - har gjort att Perl-användare blivit intresserade av Haskell och säkerligen också föranlett ett nyuppväckt intresse för Perl. Hmm, kan det vara detta som är orsaken till Perls ökning?
När det gäller TIOBE-jämförelsen av programspråk bör man notera att man studerar hur ofta ett språk nämns. Från sajten: The popular search engines Google, MSN, and Yahoo! are used to calculate the ratings. Observe that the TPC index is not about the best programming language or the language in which most lines of code have been written.
Med denna stora brasklapp i A4-format på skrivbordet kan man notera att omnämningen (användningen?) av C++ och Java har minskat jämfört med förra året. Lennart Frantzell kommenterade i Är Java-språket på fallrepet?, såvitt jag kan se utan referens till denna undersökning (varken direkt eller indirekt). Så här får han lite mer vatten på sin kvarn.
[Det skulle f.ö. vara intressant med en undersökning som studerar hur förändringar i omnämnande av ett programspråk är kopplat till förändringar av dess användningen. Troligen är det här skillnad i förändringsstruktur mellan "professionellt" användande och "privat" användande där förändringar i "professionellt" användande har dels större tröghet och dels andra krav på ett programspråk än privat utveckling. Gränsen mellan dessa två håller dock på att försvinna mer och mer i och med open source-projekten.]
En sista kommentar. I artikeln står det Many developers who must use Java or C# at work during the day go home to use Ruby or Python on their personal projects at night.
Man kan nu börja hoppas på att programspråksmoneteismen ("jag tror på ett enda programspråk och det är min gud") håller på att försvinna och att vi till slut inser att olika programspråk har olika fördelar i olika situationer/domäner.
Det är inte meningen att här starta något religionskrig om programspråk, speciellt eftersom jag numera är programspråksagnostiker (eller möjligen programspråkstaoist). Av bl.a. historiska och repositoriska skäl har jag naturligtvis ett par favoriter men kollar gärna in både nya och gamla programspråk. I går hittades t.ex. en referens till ett språk som heter Fornax (från 1994) som verkar intressant eftersom det kombinerar flera av mina favoritsyntaktiska socker; tyvärr hittades inte någon implementation.
Ingången till denna anteckning var Lambda the Ultimate:s The long tail of programming languages, vilken också bör läsas.
Posted by hakank at 10:05 FM Posted to Komplexitet/emergens | Statistik/data-analys | Systemutveckling
april 14, 2005
Digital grusväg - ännu senare nummer ute!
Husorganet Digital grusväg har återigen kommit med ett ännu mera senare nummer (1/2005 PDF).
Denna gång har specialstuderats sophinkars placering i köket. Från introduktionen:
När man vill hjälpa till att duka av bordet hemma hos en bekant, behöver man ofta slänga något i sophinken. Problemet är var sophinken är placerad. I de flesta hem finns den i skåpet under vasken, men bakom vilken av luckorna?
Undersökningens syfte var att se om det finns några uppenbara mönster bakom placeringen av sophinken i köket.
Här kommer inte att avslöjas det spännande resultatet, det får läsaren läsa själv. Däremot kan nämnas att rapporten är avundsvärt och unikt naket ärlig: Studien inbjuder till vidare forskning för att höja kunskapsnivån till en praktiskt användbar nivå. Studien konstaterat skillnader utan att kunna förklara dem.
Rapporten avslutas som sig bör med förslag till framtida studier.
Om man skulle drista sig att komma med någon kritik av undersökningen skulle det kunna vara att sophinkhinksägarens (vänster|höger-)hänthet saknas som parameter, eller snarare: den mest frekventa häntheten i hushållet samt hänthetens beskaffande, dvs om man vill öppna skåpsdörren med sin hänthetshand eller vill man slänga soporna med denna hand (cf. skyfflar en person X in mat i munnen med sin häntheta hand eller skär denne upp maten med hjälp av den).
Om det fortfarande skulle dristas med kritik kunde en annan sak nämnas, nämligen frågan om det finns något bakom den i föreliggande fall andra skåpluckan som är ännu viktigare att placera där det i så fall placerats, t.ex. tidningar för snabb access, städverktyg eller diskverktyg för ännu snabbare access, andra verktyg, eller en blå leksaksbil som används vid övriga tillfällen. Sophinkens placering och de mönster som hittades i studien skulle i så fall endast vara ett förvisso mönster, men såsom Kants teori förutspår endast visar de för oss endast flyktiga fenomen och icke Tinget i sig.
Det skulle möjligen även vara intressant med en spelteoretisk modell där man studerar fall där sophinksägaren inte vill att personer med mindre sophinksbekantskap ska hitta sophinken vid första försöket.
Läs även:
Tidigare nummer
En kort redogörelse om namnet "Digital grusväg" (främst i kommentarerna).
Posted by hakank at 05:58 EM Posted to Statistik/data-analys | Statistik/data-analys | Comments (2)
Digital grusväg - ännu senare nummer ute!
Husorganet Digital grusväg har återigen kommit med ett ännu mera senare nummer (1/2005 PDF).
Denna gång har specialstuderats sophinkars placering i köket. Från introduktionen:
När man vill hjälpa till att duka av bordet hemma hos en bekant, behöver man ofta slänga något i sophinken. Problemet är var sophinken är placerad. I de flesta hem finns den i skåpet under vasken, men bakom vilken av luckorna?
Undersökningens syfte var att se om det finns några uppenbara mönster bakom placeringen av sophinken i köket.
Här kommer inte att avslöjas det spännande resultatet, det får läsaren läsa själv. Däremot kan nämnas att rapporten är avundsvärt och unikt naket ärlig: Studien inbjuder till vidare forskning för att höja kunskapsnivån till en praktiskt användbar nivå. Studien konstaterat skillnader utan att kunna förklara dem.
Rapporten avslutas som sig bör med förslag till framtida studier.
Om man skulle drista sig att komma med någon kritik av undersökningen skulle det kunna vara att sophinkhinksägarens (vänster|höger-)hänthet saknas som parameter, eller snarare: den mest frekventa häntheten i hushållet samt hänthetens beskaffande, dvs om man vill öppna skåpsdörren med sin hänthetshand eller vill man slänga soporna med denna hand (cf. skyfflar en person X in mat i munnen med sin häntheta hand eller skär denne upp maten med hjälp av den).
Om det fortfarande skulle dristas med kritik kunde en annan sak nämnas, nämligen frågan om det finns något bakom den i föreliggande fall andra skåpluckan som är ännu viktigare att placera där det i så fall placerats, t.ex. tidningar för snabb access, städverktyg eller diskverktyg för ännu snabbare access, andra verktyg, eller en blå leksaksbil som används vid övriga tillfällen. Sophinkens placering och de mönster som hittades i studien skulle i så fall endast vara ett förvisso mönster, men såsom Kants teori förutspår endast visar de för oss endast flyktiga fenomen och icke Tinget i sig.
Det skulle möjligen även vara intressant med en spelteoretisk modell där man studerar fall där sophinksägaren inte vill att personer med mindre sophinksbekantskap ska hitta sophinken vid första försöket.
Läs även:
Tidigare nummer
En kort redogörelse om namnet "Digital grusväg" (främst i kommentarerna).
Posted by hakank at 05:58 EM Posted to Statistik/data-analys | Statistik/data-analys | Comments (2)
mars 12, 2005
"Stjärnor över änglar" - Analys av eventuella språkliga samband mellan låttitlar och deras placering i Melodifestivalen år 1959 - 2004
Introduktion till undersökningen
I söndags skrev Håkan 'hakke' Karlsson (i Med andra ord) om antal ord i titlar i lördagens melodifestival (vars deltävlingar jag inte har sett).
Detta inspirerade till följande frågeställningar (som även antyddes i kommentaren till Hakkes blogganteckning):
* Finns det något samband mellan längden på en låttitel och dess placering i en melodifestival?
* Finns det något samband mellan medellängden av titelorden och dess placering i en melodifestival?
* Finns det överhuvudtaget något samband mellan titlar och något annat?
Kort summering: Nej, det finns inga sådana samband. Med ett undantag: den genomsnittliga längden på orden har blivit något kortare med åren.
Rubriken "Stjärnor över änglar" får sin förklaring i någon av nedanstående avsnitt. Läs vidare.
Introduktion av data
Efter lite letande på nätet hittades det låttitlar och deras placeringar i Melodifestivalen för åren 1959 till 2004; alla mellanliggande år har dock inte varit behäftade med melodifestivaler.
Som vanligt tog pre-processingen av datan mest tid, filtrera informationen på ett sätt som gör att det gick att bearbeta med analysprogram, i detta fall - och som vanligt - det fria systemet R.
Lite översiktlig information om datan:
* 406 låttitlar i 43 melodifestivaler har studerats
* Det var 1305 unika ord
* Det finns ett flertal varianter för poängberäkning, t.ex. med 10 låtar där endast 5 fått en placering, en variant (1959) där samma artist (Ingvar Wixell) sjöng alla låtar etc etc. Jag har dock försökt att normalisera placeringarna till poäng, se "Ordpoäng" nedan.
Konkordanstabeller
Förutom ren statistisk analys (eller snarare data snooping) som ju inte gav så mycket, gjordes även lite andra analyser, t.ex. konkordanstabeller över antal förekomst av orden i titlarna.
Här är de vanligaste orden samt antalet antal låttitlar som har innehåller detta ord. Notera att även om ett ord finns flera gånger i en låttitel räknas det bara en gång (dubletter räknas alltså inte dubbelt, se även nedan).
ord: antal
en: 44
jag: 37
du: 35
mig: 30
är: 28
dig: 27
i: 24
det: 23
och: 20
som: 18
om: 16
min: 14
på: 13
sång: 12
här: 11
vår: 9
kärlek: 8
till: 8
se: 8
för: 7
mitt: 7
med: 7
bara: 7
igen: 7
vän: 7
vill: 6
gång: 6
av: 6
har: 6
finns: 6
kommer: 6
nu: 6
när: 6
din: 6
ska: 5
dina: 5
var: 5
hand: 5
inte: 5
vals: 5
vi: 5
kärleken: 5
ett: 5
dröm: 5
värld: 5
liv: 5
stjärna: 4
över: 4
änglar: 4
ger: 4
alla: 4
ha: 4
världen: 4
så: 4
natten: 4
livet: 4
ser: 4
att: 4
hos: 4
gör: 4
allt: 3
eld: 3
annan: 3
spela: 3
stanna: 3
Vilket nog skulle kunna bli en bra - måhända existentiell - sångtext:
En jag, du mig.
Är dig i det och som om min.
På sång här vår kärlek till,
se för mitt, med bara igen: vän.
Vill gång av.
Har? Finns?
Kommer nu när din ska;
dina var hand.
Inte vals, vi.
Kärleken ett,
dröm, värld, liv
Stjärna över änglar,
ger alla ha.
Världen så natten livet.
Ser att hos gör allt, eld annan spela.
Stanna!
(Jag tycker speciellt om "stjärna över änglar". googleförekomst: 0.)
"Ordpoäng"
Så till en lista över genomsnittlig "ordpoäng", dvs hur många poäng har ett ord fått under åren.
Två kommentarer:
Poäng är här uträknat som: antal låtar i tävlingen - placering + 1
Det innebär att låt på första platsen av 6 låtar får 6 poäng (6 - 1 + 1 = 6), andra platsen vid en tävling av 10 låtar får 9 poäng (10 - 2 + 1 = 9) etc. För tävlingar med utslagningar har de utslagna låtarna fått tillräkna sig 1 poäng.
Den andra kommentaren är att ord som endast förekommit en gång i en sång titel är borttagna, annars skulle ord som "satellit", "cocacola" och "bugg" (vilka är ord som endast förekommit en gång i en vinnande låt) komma först och det vill vi ju inte.
ord: genomsnittlig poäng, antal poäng, antal ord
dag: 10.00, 30, 3
your: 9.50, 19, 2
let: 9.50, 19, 2
dé: 9.00, 18, 2
vackraste: 9.00, 18, 2
é: 9.00, 18, 2
love: 8.50, 17, 2
bang: 8.50, 17, 2
stad: 8.00, 16, 2
hallå: 8.00, 16, 2
havet: 8.00, 16, 2
härliga: 8.00, 16, 2
över: 7.75, 31, 4
vindarna: 7.67, 23, 3
fångad: 7.50, 15, 2
varje: 7.50, 15, 2
vilken: 7.00, 14, 2
älskar: 7.00, 14, 2
härlig: 7.00, 14, 2
vem: 7.00, 14, 2
sången: 7.00, 14, 2
dansa: 7.00, 21, 3
april: 7.00, 14, 2
hela: 6.50, 13, 2
is: 6.50, 13, 2
hej: 6.50, 13, 2
Ordmultiplicitet
Påverkas placeringen av förekomsten av dubbletter i titeln? Möjligen finns det en liten fördel med dubletter: ord som förekommer fler än en gång i en låttitel har en genomsnittliga poäng på 4.57 medan enkelord har genomsnittligt 4.39 poäng. Om det är ett samband så är det svagt.
Finns det något samband, då?
Så var det där med de ursprungliga frågeställningarna om sambanden mellan låttitelns ord och låtens placeringen. Det fanns ingen. Inte heller finns något av följande samband (eller så hittade jag dem inte):
* antal ord i låttiteln
* medelantalet ord i låttiteln
* antal tecken i låttiteln
* huruvida det finns dublettord i titeln eller inte (men se ovan)
Förändring av medellängden av ord över åren
Det finns dock en liten förändring av medellängden på orden över åren. För hela perioden (1959-2004) har medellängden minskat från cirka 5.5 bokstäver per ord till cirka 4 bokstäver per ord (detta inkluderat siffror och talspråksvarianter som "de'" i stället för "det"), och det kanske säger en del om vår kultur i allmänhet, även om jag inte tror att melodifestivalen någonsin har varit en kulturens högborg. (En mer seriös fråga: har medelantalet tecken per ord i normal text minskad i samma omfattning över åren? )
Bilden visar denna utvecklingen av medellängden per ord, där den räta linjen är regressionslinjen.
R-kod för analysen
Här är lite R-kod för att skapa bild och analysen av medellängden per år. Kontentan är att för varje år minskar ordens medellängd med cirka 0.02 tecken. Det låga värdet på Adjusted R-squared (0.27) påvisar att det är lågt förklaringsvärde; p-värdet är < 0.001.
# läs in data över årems genomsnittliga längd
> melodi.year <- read.table("melodi_year.dat", sep=",", header=T)
# gör en linjär analys
> summary(lm(aver_letters_per_words~year, data=melodi.year))
Call:
lm(formula = aver_letters_per_words ~ year, data = melodi.year)
Residuals:
Min 1Q Median 3Q Max
-0.98296 -0.30508 -0.03489 0.22848 0.85569
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 45.220494 9.720366 4.652 3.41e-05 ***
year -0.020288 0.004903 -4.138 0.00017 ***
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 0.4278 on 41 degrees of freedom
Multiple R-Squared: 0.2946, Adjusted R-squared: 0.2773
F-statistic: 17.12 on 1 and 41 DF, p-value: 0.0001699
# plotta
> plot(aver_letters_per_words~year, data=melodi.year)
# visa regressionslinjen
> abline(lm(aver_letters_per_words~year, data=melodi.year))
För att testa modellen görs slutligen en prediktion för år 2005: den genomsnittliga ordlängden blir enligt modellen 3.84 tecken per ord.
# prediktion för år 2005
> round(predict(lm(aver_letters_per_words~c(year-1960), data=melodi.year),data.frame(year=2005)),2)
[1] 3.84
Det korrekta medelvärdet är 4.07, och med skillnaden på 4.07 - 3.84 = 0.23 är det lite väl mycket fel för att modellen ska accepteras som en god approximation (vilket vi nog visste ändå).
Slutord
Det finns mängder av annan analys man skulle kunna göra:
* hur är orden fördelade över åren? T.ex. är titelordet "en" vanligare nu än på 60-talet? Kom sångtitlar med "sång" bättre än på 90-talet än på 80-talet?
* man kan även ta med aristens kön i kombination med ord, t.ex. har titelordet "kärlek" sjungen av en man (eller flera män) bättre placering är då den besjunges av en kvinna (eller flera kvinnor) eller av en blandad grupp (man/män + kvinna/kvinnor)?
* påverkar låttitlarnas (och framförallt vinnarens) språkliga sammansättning nästa års låttitlar? Det skulle här vara möjligt att göra tidsserieanalyser. En mycket preliminär analys visar att det möjligen finns ett sådant samband (autokorrelation), och det förvånande är att påverkan verkar vara något större två år senare än det omedelbart efterföljande året.
En bild där punkterna sammanbundna med linjer visar möjliga ansatser kring tidsserieanalyser, t.ex. att studera de där dipparna i slutet av 1960-, 1980- samt 1990-talet vilka omedelbart föregicks av ett rätt högt medelvärde.
* finns det motsvarande samband/icke-samband mellan t.ex. filmtitlarna och hur bra det gått för filmerna.
Ja, det finns mycket att analysera. Men troligen visar sådana analyser inte speciellt mycket mer samband än de föreliggande analyserna mer än möjligen en allmän förändring av språkbruket över åren.
Melodifestivalerna är ju trots allt inte en tävling i låttitlarnas språkligheter utan i mycket annat, t.ex. artist, dennes/deras utstrålning, kläder (eller avsaknaden av dem); möjligen är musiken och själva texten också avgörande för hur bra en låt blir placerad.
Posted by hakank at 11:47 FM Posted to Statistik/data-analys | Comments (12)
mars 02, 2005
Internetworlds bloggomröstning: En halvtidsanalys
Så här ungefär i halvtid av Internetworlds Bästa-bloggen-omröstning, (och som skrevs om i Internetworld: "Rösta fram Sveriges bästa blogg") passar det kanske bra med en liten analys av besökarbeteendena, dvs hur besökarna från omröstningssidan betett sig,
Först några summerande tal för besöken mellan första dagen 17 februari till och med cirka klockan 18 idag (2 mars):
* Det har klickats 255 gånger från omröstningssidan till hakank.blogg.
* Det som har besökt via omröstningssidan har besökt totalt 556 sidor, vilket ger ett medelvärde på 2.1 sidor per besök.
* Totalt gjordes det 99 extra besök, vilket utgör en "effektivitet" på cirka 18%: extra besök/totalt antal = 88/556 ~ 0.18.
Tabellen nedan visar antal sidor som besöktes på bloggen efter omröstningsklicket, samt antalet besökare som klickade så många extra sidor:
| Antal extra sidor | Antal besökare med detta beteende |
|---|---|
| 0 | 217 |
| 1 | 18 |
| 2 | 9 |
| 3 | 6 |
| 4 | 2 |
| 10 | 1 |
| 12 | 1 |
| 15 | 1 |
Dvs av de 255 besökare gjorde 217 inget extraklickande alls. Visst är det deprimerande. Det var 18 stycken som klickade vidare 1 gång, 9 som klickade på ytterligare 2 sidor osv. Jag hade nästan hoppats att de skulle rota omkring ordentligt på bloggen. Skoj att det i alla fall var ett par tre stycken som rockade loss lite mer i alla fall.
Not: En del av besöken var proxies (dvs att flera besökare använder samma IP-adress) som gör att värdena är lite missvisande, men det är sånt man får leva med. Åtminstone två av loss-rockarna är inte proxies, däremot misstänker jag att de själva är bloggare.
Slutsats?
Frågan är vilken slutsats man ska dra om detta. En slutsats kan vara att besökarna tyckte att det var så (o)intressant att det gick att göra en vettig bedömning om innehållet, vilket måhända är sant. En annan slutsats, i samma anda, är att det troligen inte är så mycket som lockar en besökare att "rota runt". Man skulle kunna tänka sig att skriva lite mer publikfriande saker nu när det kan komma fint besök, men jag tror inte riktigt på sådant. Då är det bättre att skriva på som vanligt.
En annan förklaring kan ju vara att besökarna redan besökt bloggen tidigare och ville bara kolla så att det var den blogg som de trodde. Men det är en alldeles för otrolig förklaring.
Helt enkelt är det precis så här vi beter oss igemen, hittar vi inte direkt intressant så går vi snabbt därifrån.
Notera att besöksbeteendet på en blogg beror också en hel del på vilka anteckningar som råkar vara överst vid ett besök. Det har jag dock inte kalibrerat in i beräkningarna.
En mer detaljerad analys
Så kommer en mer detaljerad analys av beteendet som har en något annan beräkning än ovanstående, men slutsatsen är samma som ovanstående: Det är väldigt många som endast kollar på första sidan och vänder i dörren.
I dessa värden har inkluderats besöken från hela februari, dvs även sådana som gjorts innan omröstningen (dvs från 1:e februari till den 17:e). Detta för att få en mer fullständig bild av besökandet.
Först en tabell på antal sidor man varit inne på hakank.blogg (kolumnen "Hits"), inkluderat sådana som besökts före första klicket från omröstningssidan (t.ex. via sökmotorer etc). Kolumnen "First" anger vilket besök i ordningen som var besöket från omröstningssidan. "Count" är så många besökare som haft detta beteende.
Det innebär alltså (för första raden) att det varit 193 besökare som besökt en (1) sida ("Hits"), och detta besök var det direkt efter klicket från omröstningssidan. Två rader ner ser vi att det varit 11 stycken som fortsatte att klicka på en sida på bloggen. Någonstans bland de sista raderna ser vi att någon varit inne på bloggen 80 gånger tidigare, den 81:e gången via omröstningssidan, och klickade vidare några sidor. Denna sistnämnda är en proxy men det tar jag ingen som helst hänsyn till.
Den sista kolumnen "Rate" är ett sätt att mäta "effektiviteten" i omröstningsklicket, och som räknas enligt formeln:
(antalet besökta sidor - när första besöket gjordes)/ (antalet besökta sidor)
Exempel: Om en besökare besökt bloggen 3 gånger och den tredje gången var via omröstningssidan räknas "effektiviteten" enligt samma princip som ovanstående: (3-3)/3 = 0/3 = 0. En besökare som besökt bloggen 4 gången och det via omröstningssidan var på första besöket blir det (4-1)/4 = 3/4 = 0.75.
| First | Hits | Count | Rate |
|---|---|---|---|
| 1 | 1 | 193 | 0.00 |
| 2 | 2 | 13 | 0.00 |
| 1 | 2 | 11 | 0.50 |
| 1 | 3 | 5 | 0.67 |
| 5 | 5 | 4 | 0.00 |
| 1 | 4 | 3 | 0.75 |
| 4 | 4 | 3 | 0.00 |
| 2 | 3 | 3 | 0.33 |
| 5 | 7 | 2 | 0.29 |
| 7 | 7 | 2 | 0.00 |
| 3 | 3 | 2 | 0.00 |
| 3 | 4 | 2 | 0.25 |
| 5 | 6 | 1 | 0.17 |
| 4 | 5 | 1 | 0.20 |
| 81 | 85 | 1 | 0.05 |
| 8 | 10 | 1 | 0.20 |
| 3 | 15 | 1 | 0.80 |
| 3 | 5 | 1 | 0.40 |
| 2 | 17 | 1 | 0.88 |
| 1 | 5 | 1 | 0.80 |
| 13 | 23 | 1 | 0.43 |
| 7 | 10 | 1 | 0.30 |
| 16 | 19 | 1 | 0.16 |
| 2 | 5 | 1 | 0.60 |
Till slut kommer en summering av ovanstående tabell, där rate är sorteringsordningen och Count anger hur många som hade en viss rate (besökseffektivitet).
| Rate | Count |
|---|---|
| 0.88 | 1 |
| 0.80 | 2 |
| 0.75 | 3 |
| 0.67 | 5 |
| 0.60 | 1 |
| 0.50 | 11 |
| 0.43 | 1 |
| 0.40 | 1 |
| 0.33 | 3 |
| 0.30 | 1 |
| 0.29 | 2 |
| 0.25 | 2 |
| 0.20 | 2 |
| 0.17 | 1 |
| 0.16 | 1 |
| 0.05 | 1 |
| 0.00 | 217 |
Som sagt, man kan dra samma slutsats som för första tabellen. Skillnaden är att de två sista tabellerna visas de olika beteendena mer detaljerat.
Allra-sist-kommentar
För den som nu oroar sig att jag suttit och handräknat de uppkomna värdena: Oroen er icke! Ovanstående är resultatet av dels ett generellt program (nyligen optimerat och med en massa bells 'n whistles) för att studera webbserverloggen, dels ett mer specialdesignat program för att göra ovanstående uträkningar.
Posted by hakank at 10:17 EM Posted to Blogging | Statistik/data-analys | Comments (4)
december 12, 2004
Fraktalbloggare?
I Artikeln om bloggning i InternetWorld myntar Annica Tiger begreppet "Nollbloggar" (och hon utvecklar detta lite i Nollbloggar). Betydelsen är att i många bloggar kommenteras det aldrig eller mycket sällan i. Den förstnämnda artikeln är skriven - bör noteras - med glimten i ögat, men med en viss ironi (och detta motto torde väl stå för den innevarande blogganteckningen också).
Annica Tigers blogg tillhör ju den andra gruppen bloggar, dvs den där det alltid är fullt med långa diskussioner och dit man gärna går och läser. Men vad ska man kalla sådana bloggar som Annicas, dvs motsatsen till noll-bloggar? Kanske "Ett-bloggar"?
Kommen så långt i tankarna kom begreppet "fraktal-bloggar" upp. Det skulle motsvarar de bloggar som ligger mitt emellan de båda extremerna: har ibland många kommentarer men oftast är det inga eller ett fåtal.
Steget till att undersöka hur det ligger till med detta för en näraliggande blogg var naturligtvis inte långt. Så här är fördelningen av antal kommentarer på hakank.blogg och hur många blogganteckningar som har detta antal kommentarer.
Antal kommentarer: Antal anteckningar
0: 498
2: 66
1: 50
4: 35
3: 34
5: 19
6: 10
8: 10
7: 7
9: 4
10: 3
11: 2
14: 2
21: 1
12: 1
23: 1
Förklaring: Det finns 498 blogganteckningar som har 0 kommentarer, 66 anteckningar med 2 kommentarer osv. Samt en långkörare med 23 kommentarer; glädjande nog en som eventuellt fortfarande pågår: Skånsk bloggaremiddag: en sammanfattning.
(Man kan här notera att det finns fler anteckningar med 2 kommentarer än med 1 kommentar, och fler med 4 kommentarer än med 3 Detta beror på att jag försöker att svara på alla kommentarer så en gästkommentarer resulterar i en egen kommentar, in alles 2. Att det är så pass många som 50 anteckningar med endast en kommentar är lite skamligt.)
Här är en bild som åskådliggör detta. Den röda linjen är ett försök att göra en linjär regression över datan.
Som förklarades mer i den liknande analysen Statistikknarkande: Antal webb-besökare och power law kan man räkna ut en koefficient för denna regressionslinje, vilket för den nu studerade datan är 2.33.
Alltså: Jag är en (fraktal) 2.33-bloggare!
För mer information om power laws och fraktaler hänvisas till den ovan nämnda Statistikknarkande: Antal webb-besökare och power law.
Man bör dock komma ihåg nedanstående citat från Mandelbrot (citerades bl.a. i Benoit Mandelbrot intervjuad i New Scientist: A fractal life) som tar udden ur en del av fraktal/power law-forskningen: [Question:] Fractals seem to appear all over nature and in economics. Even the internet is fractal. What does that say about the underlying nature of these phenomena?
[Mandelbrot:] Well, it depends on the field. Circles and straight lines also appear everywhere. Does this mean that all those phenomena have something in common? Of course not. The roughly circular trajectory of a planet around the sun is due to gravitational interactions. Berries are round because a sphere has a smaller skin. The beauty of geometry is that it is a language of extraordinary subtlety that serves many purposes.
Lustigt nog fick hakank.blogg (bland andra) ett annat värde idag, nämligen 0.36. Det var i Lemonad-jonas o/ordning-anteckning cirkelresonemang 2. Värdet gäller förhållandet mellan antal länkar i blogganteckningarna och antal länkar till sin egent blogg. (Jag funderar fortfarande vad detta värde egentligen innebär och återkommer till Jonas om något kommes på.)
Så på samma dag helg har vi fått två matematiska dimensioner för bloggar:
* antal självrefererande länkar
* fördelningen av kommentarer
Ska vi försöka hitta en tredje så att det blir en fin tredimensionell modell?
Posted by hakank at 12:11 FM Posted to Blogging | Statistik/data-analys | Comments (14)
december 11, 2004
Monte Carlo Simulation in Excel: A Practical Guide
Monte Carlo Simulation in Excel: A Practical Guide:
Monte Carlo simulation is often used in business for risk and decision analysis, to help make decisions given uncertainties in market trends, fluctuations, and other uncertain factors. In the science and engineering communities, MC simulation is often used for uncertainty analysis, optimization, and reliability-based design. In manufacturing, MC methods are used to help allocate tolerances in order to reduce cost. There are certainly other fields that employ MC methods, and there are also times when MC is not practical (for extremely large problems, computer speed is still an issue). However, MC continues to gain popularity, and is often used as a benchmark for evaluating other statistical methods.
This article will guide you through the process of performing a Monte Carlo simulation using Microsoft Excel. Although Excel will not always be the best place to run a scientific simulation, the basics are easily explained with just a few simple examples.
Se även
The Basics of Monte Carlo Simulations
MathWorld: Monte Carlo Method (med referenser)
Posted by hakank at 08:45 EM Posted to Statistik/data-analys
november 07, 2004
Persi Diaconis-föreläsning: Conditioned Limit Theorems
Att kolla in mer vid tillfälle.
Persi Diaconis-föreläsning: Conditioned Limit Theorems:
Keywords : Analysis of algorithms; poissonization; conditioned limit theory; Lecams method; Bayes theory; definettis theorem.
Abstract : Poissonization can be abstracted to a wide ranging method for randomizing a perimeter to make components independent. This allows us to handle exponential structures, random matrices and much else. There are many ways of derandomizing. I will feature Bayes theorem and Lecams method.
Posted by hakank at 08:03 FM Posted to Statistik/data-analys
Kartor över det amerikanska valet: Diffusion-based method for producing density equalizing maps
Michael Gastner, Cosma Shalizi, and Mark Newman: Maps and cartograms of 2004 US presidential election results visar och diskuterar olika typer av kartor för att representera resultet av det amerikanska valet. För fina bilder, se artikeln.
The states of the country are colored red or blue to indicate whether a majority of their voters voted for the Republican candidate (George W. Bush) or the Democratic candidate (John F. Kerry) respectively. (Hawaii and Alaska are not shown on the map.) The map gives the superficial impression that the "red states" dominate the country, since they cover far more area than the blue ones. However, as pointed out by many others, this is misleading because it fails to take into account the fact that most of the red states have small populations, whereas most of the blue states have large ones. The blue may be small in area, but they are large in terms of numbers of people, which is what matters in an election.
...
The cartogram was made using the diffusion method of Gastner and Newman, which is described in detail in this article. Population data were taken from the 2000 US Census. Iowa and New Mexico, which at the time of writing were officially undeclared, we have assumed to have a Republican majority -- all indications are that this will be the final declaration once recounts are complete.
The cartogram reveals what we know already from the news: that the country was actually very evenly divided by the vote, rather than being dominated by one side or the other.
Algoritmen som nämns i artikeln finns i:
Michael T. Gastner, M. E. J. Newman: Diffusion-based method for producing density equalizing maps
Abstract:
Map makers have long searched for a way to construct cartograms -- maps in which the sizes of geographic regions such as countries or provinces appear in proportion to their population or some other analogous property. Such maps are invaluable for the representation of census results, election returns, disease incidence, and many other kinds of human data. Unfortunately, in order to scale regions and still have them fit together, one is normally forced to distort the regions' shapes, potentially resulting in maps that are difficult to read. Many methods for making cartograms have been proposed, some of them extremely complex, but all suffer either from this lack of readability or from other pathologies, like overlapping regions or strong dependence on the choice of coordinate axes. Here we present a new technique based on ideas borrowed from elementary physics that suffers none of these drawbacks. Our method is conceptually simple and produces useful, elegant, and easily readable maps. We illustrate the method with applications to the results of the 2000 US presidential election, lung cancer cases in the State of New York, and the geographical distribution of stories appearing in the news.
Via Cosma Shalizi (Three-Toed Sloth): Decided and Divided Americas
Posted by hakank at 07:06 FM Posted to Statistik/data-analys
oktober 19, 2004
Ivars Peterson: Randomness, Risk, and Financial Markets
Math Trek: Randomness, Risk, and Financial Markets, Science News Online, Oct. 9, 2004:
Pi, the ratio of a circle's circumference to its diameter, is known as an irrational number because it can't be exactly expressed as a ratio of whole numbers. It would take an infinite number of digits to write it out in full as a decimal or, in binary form, as a string of 1s and 0s. The square root of 2, the square root of 3, and the constant e (the base of the natural logarithms) fall into the same category.
The known digits of these numbers appear patternless. According to one novel method of assessing the randomness of a sequence of numbers, however, the digits of pi turn out to be somewhat more irregular than the digits of the other irrational numbers.
The measure used to determine the irregularity or degree of disorder (entropy) of these sequences is called the approximate entropy. Invented by Steve Pincus of Guilford, Conn., and developed in cooperation with Burton H. Singer of Princeton University, this measure characterizes the randomness of a sequence of numbers.
...
For example, Pincus has looked at stock market performance, as measured by Standard and Poor's index of 500 stocks. His calculations show that fluctuations in the index's value are generally quite far from being completely irregular, or random.
Flera referenser till Pincus och Singer finns i artikeln.
Posted by hakank at 06:53 FM Posted to Statistik/data-analys | Comments (1)
oktober 06, 2004
R version 2.0.0 och ett nytt nyhetsbrev
Häromdagen kom version 2.0.0 av statistik- och dataanalyssystemet R och igår kom en färdigkompilerad Windowsversion.
Idag kom septembernumret av R News (PDF-fil) som bl.a. handlar om en av de nya finesserna i 2:an, nämligen "lazy loading". Ett annat avsnitt är om Rgraphviz som hanterar grafer, och exemplifieras med "molecular pathways". I slutet listas alla de nya funktionerna för 2:an och de paket som kommit sedan förra numret.
Posted by hakank at 08:24 EM Posted to Statistik/data-analys | Comments (1)
september 02, 2004
Analys av påstått valfusk i Venezuela
Folkomröstningen i Venezuela påstås har varit utsatt för valfusk. Några amerikanska dataloger har gjort en statistisk analys av röstdatan, och hittar inget som stödjer att det tyder på att det är något statistisk ovanligt. Det kan naturligtvis - som de skriver - vara fråga om någon annan typ av fusk (se nedan) .
På www.venezuela-referendum.com finns papret Analysis of Voting Data from the Recent Venezuela Referendum, skrivet av Edward W. Felten, Aviel D. Rubin samt Adam Stubblefield. Det är hållet på en pedagogisk nivå som förklarar metoderna som använts.
Abstract (mina emfaser):
After the August 15 referendum in Venezuela on whether or not to recall president Chávez, opposition groups examined the polling data and made accusations of fraud due to statistical anomalies in the reported election results that they claim could not have occurred if the election were run fairly. However, our analysis of the same data, based on simulations, did not detect any statistical anomalies that would indicate obvious fraud in the election.
We emphasize that a lack of statistical evidence does not imply the absence of fraud. Rather, it rules out certain classes of fraud. In any case, the fraud that is alleged is not the type that we would expect a cheating government to employ. In particular, we believe that the forms of election fraud that are most likely to succeed, such as voting machines silently switching some fraction of Yes votes to No votes inside the computer, would not produce observable statistical anomalies.
Electronic voting is more susceptible to widespread fraud than less automated mechanisms. The fact that the opposition is highly suspicious of the outcome is due, in part, to the choice of electronic voting machines in a simple Yes/No election. While we did not find any statistical evidence for the claims of caps on the machines or other specific accusations of fraud, we are concerned that wide scale unobservable fraud is much easier to realize in electronic voting machines than in, for example, precinct based paper systems.
På samma sida kan man ladda ner en datafil om man vill göra egna analyser. (Det finns även ett Python-program men det var tyvärr inte fullständigt.)
Via EurekAlert!
Posted by hakank at 06:58 EM Posted to Statistik/data-analys | Comments (7)
augusti 30, 2004
John Allen Paulos om en förutsägelse av det amerikanska valet
I Election Prediction - Four More Years or Four More Variables? beskriver och kritiserar John Allen Paulos en av förutsägelserna av det amerikanska valet.
A well-known Yale economist has written a book using the mathematical technique of regression to predict the outcome of presidential elections. Ray C. Fair's Predicting Presidential Elections and Other Things grew out of his 1978 paper that provides quite accurate descriptions of these quadrennial elections dating back to 1916. Before getting to his very surprising prediction for this November (with which I disagree), let me sketch the idea behind the technique.
Sedan går Paulos Igenom de olika parametrarna som Fair använder för att förutsäga valets utgång, och slutsatsen blir:
The bottom line: the model predicts that the outcome won't even be close. Bush will win somewhere around 58 percent of the vote.
This is quite contrary to the polls and to the election futures markets, both of which indicate a very tight race. Still, before dismissing Fair's prediction out of hand, note that his model has been impressive (in retrospect) over the 22 presidential elections since World War I. Although the model's predictions of the victor were wrong in a couple of very close elections, its predictions of the vote percentages in these years were nevertheless quite accurate.
Men Paulos är kritisk till modellen eftersom den inte tar hänsyn till flera viktiga parametrar:
...
I suspect that other variables — the war in Iraq, cultural and environmental issues, and concerns about civil liberties — will play a more important role in this year's election than in past years, and they are not part of Fair's model. Even the economic factors in his model fail to reflect anxieties over job losses, huge deficits, and increasingly disproportionate inequalities of income.
Han är även principiellt kritiskt till denna typ av regressionsmodeller, vilket även diskuteras. Artikeln avslutas på följande sätt:
The prediction of Fair's model that Bush will win by a wide margin is likely to be disturbing to Kerry supporters and heartening to Bush supporters. Because of the anomalous nature of this election, the testimony of the polls and the election markets, and the frequent unreliability of regression models, however, I do not believe it.
We'll just have to wait until November (or, horrors, December) to see whether Professor Fair's model will be outfitted with new variables and, a bit more importantly, the country outfitted with a new president.
Posted by hakank at 07:39 EM Posted to Statistik/data-analys | Comments (2)
juni 30, 2004
Straffsparkar i fotboll och annan fotbollsmatematik
Apropå de många straffarna i fotbolls-EM.
Följande paper är en spelteoretisk modell av straffsparkar (ganska teknisk och har ännu inte luslästs):
P.A. Chiappori, S. Levitt, T. Groseclose: Testing Mixed Strategy Equilibria When Players Are Heterogeneous: The Case of Penalty Kicks in Soccer (PDF).
Abstract
This paper tests the predictions of game theory using penalty kicks in soccer. Penalty kicks are modelled as a variant on matching pennies in which both the kicker and the goalie choose one of three strategies: left, middle, or right. We develop a general model allowing for heterogeneity across players and demonstrate that some of the most basic predictions of such a model survive the aggregation necessary to test the model using real-world data, whereas others do not. We then present and test a set of assumptions su¢cient to allow hypothesis testing using available data. The model yields a number of predictions, many of which are non-intuitive (e.g. that kickers choose middle more frequently than goalies). Almost all of these predictions are substantiated in data from the French and Italian soccer leagues. We cannot reject the null hypothesis that players are behaving optimally given the opponent's play.
En av författarna till ovanstående paper, Steven Levitt, har skrivit andra skoj saker; tyvärr inte kostnadsfritt nedladdningsbara.
Ovanstående länkar: via Full Context
Lite mer efterforskningar ledde bl.a. till nedanstående om fotbollsmatematik
John Haigh, författare till boken Taking Chances: Winning With Probability, har skrivit några essäer om fotbollsmatematik.
Blast it like Beckham?. En spelteoretisk analys av straffsparkar, men ska nog ses som en introduktion till spelteori snarare än en vetenskaplig analys av straffsparkar.
On the ball innehåller däremot mer empiriska rön.
Om tiderna för målens läggande (som funderades kring i Optimering av fotbollstittande):
Data collected from professional soccer matches suggest strongly that the
times when goals are scored are fairly random, with two minor
modifications: more goals are scored, on average, in a given five-minute
period late in the game than earlier; and "goals beget goals" in the sense
that the more goals that have already been scored up to the present time,
the greater the average number of goals in the rest of the match. But
these two points are second order factors: by and large, the simple model
which assumes that goals come along at random at some average rate, and
irrespective of the score, fits the data quite well.
Om sannolikheten för ett lag att vinna matchen om det lägger första målet:
So in the Premiership, indeed most professional soccer, we expect a team
to win about 2/3 of the games in which it scores first, and draw about 1/5
of them. That offers the warm comfort that if your team scores first, it
should lose only about one time in seven. You can check the match outcomes
each week, and over a season, from information in the newspapers. Real
data do conform well to these proportions.
För övrigt är Plus Magazine en mycket intressant sajt för den som vill läsa denna typ av artiklar. Fler spelteoriartiklar från Plus Magazine finns här.
Några andra skrifter på samma tema:
Game Theory: Additional Topics, Shooting at the goalkeeper. Kort exempel.
Kicker/goalie = pitcher/batter
Professionals Play Minimax: Appendix (PDF),
Posted by hakank at 08:01 EM Posted to Statistik/data-analys
juni 25, 2004
Mona Lisas leende
New Scientist Noisy secret of Mona Lisa's smile:
For centuries, artists, historians and tourists have been fascinated by Mona Lisa's enigmatic smile. Now it seems that the power of Leonardo da Vinci's masterpiece comes in part from an unlikely source: random noise in our visual systems.
...
As would be expected, noise that lifted the edges of her mouth made Mona Lisa seem happier, and those that flattened her lips made her seem sadder. More surprising though, was how readily the visual noise changed people's perception of the Mona Lisa's expression.
I artikeln finns även en serie bilder där leendet har blivit manipulerat för att visa andra uttryck än det hemlighetsfulla.
En något annorlunda presentation av ovanstående finns i Daily Times-artikeln Snow, the secret of Mona Lisa’s smile.
De lyckliga själar som har Science Direct-konto kan läsa papret från Vision Research, Volume 44, Issue 13. Det heter "What makes Mona Lisa smile?" [NB: Eftersom sådant konto saknas har papret inte lästs. Papret har nu erhållits. Stort tack!]
Abstract
To study the ability of humans to read subtle changes in facial expression, we applied reverse correlation technique to reveal visual features that mediate understanding of emotion expressed by the face. Surprising findings were that (1) the noise added to a test face image had profound effect on the facial expression and (2) in almost every instance the new expression was meaningful. To quantify the effect, we asked naïve observers to rank the face of Mona Lisa superimposed with noise, based on their perception of her emotional state along the sad/happy dimension. Typically, a hundred trials (with 10 or more samples for each rank category) were sufficient to reveal areas altering the facial expression, which is about two orders of magnitude less than in the other reverse correlation studies. Moreover, the perception of smiling in the eyes was solely attributable to a configurational effect projecting from the mouth region.
Posted by hakank at 07:58 FM Posted to Statistik/data-analys | Comments (1)
juni 18, 2004
Optimering av fotbollstittande, nya rön I
I Optimering av fotbollstittande efterfrågades statistik över mål i fotbollsmatcher för att kunna optimera sitt tittande. Originalanteckningen är nu uppdaterat med de nya rön som framkommit.
Posted by hakank at 07:29 EM Posted to Statistik/data-analys
juni 15, 2004
Optimering av fotbollstittande
Såg till min glädje den andra halvleken av Sverige-Bulgarien-matchen i går kväll (och såg alltså 4 svenska mål!), trots att jag inte är så väldigt intresserad av fotboll.
Det fick mig att tänka på om man kunde optimera sitt fotbollstittande på något sätt. Målet är alltså att se så många mål som möjligt under kortast möjliga tid. I direktsändning. Förslaget att bara se repriserna eller sammandraget efter matchen är kreativt men missar poängen.
En à priorisk länstolsanalys: Man skulle kunna tänka sig att det kommer fler mål i andra halvlek än i första, och fler mål senare i en halvlek är tidigare. Å andra sidan tenderar väl slutet på andra halvlekar med 1-målsledningar att vara tråkiga då det ledande laget mesar och försöker att befästa sin position. Å tredje sidan försöker det förfördelade laget då pressa på för att det ska bli oavgjort. Etc.
Så, en öppen fråga: Finns det gjort någon statistisk analys över fördelningen av hur många fotbollsmål som görs under respektive spelminuter? Låt oss begränsa det till VM och/eller EM för enkelhetens skull (om det blir enklare).
Fråga kopplat till den nämnda optimeringen: Om man endast vill/kan/får titta på en match i två avsnitt om 15-minuter, vilka 15-minutersavsnitt ska man då välja för att det är störst chans att se många mål?
google-research
Det gjordes naturligtvis lite research kring detta. Varpå bl.a. följande hittades.
Using Soccer Goals to Motivate the Poisson Process (PDF), en skoj sak innehåller en del av det som efterfrågas, men fokuserar på tidintervallen mellan målen i stället för många mål som görs under en viss spelminut. (Det finns en viss relation mellan dessa två mätvärden, men jag skulle gärna vilja ha så "ren" data som möjligt.)
Tyvärr hittades inte den Excelfil som det talas om. Det hänvisas till data på sajten Fifa's World Cup som i och för sig verkar trevlig, men inte katten hittar jag någon relevant data.
I papret hänvisas även till en introduktion till Poissonfördelningar: Shark attacks and the Poisson approximation (PDF).
Annat som hittades när det letades:
A game theoretic view on soccer (PDF)
Daily Play at A Golf Course: Using Spreadsheet Simulation to Identify System Constraints.
Uppdatering 2004-06-18
Via källor - som vanligtvis är säkra, men just i detta speciella fall inte anser sig så väldigt säkra - rapporteras följande. Tack Wille och Jonas!
I onsdags var just detta uppe på tapeten i "hanssons historia" inför matchen Ryssland - Portugal-matchen. En av källorna berättade att denne har för sig att Hansson berättade ungefär följande om hittilsvarande mål i detta EM:
- ett mål var 44 minut under ordinarie tid.
- ett mål var 20 minut under de sista 10, dvs varannan match blir det mål de sista 10 minuterna
- ett mål var 10 minut under tilläggsminuter.
samt att detta EM så lång var extremt vad gällde sena mål.
Ja, det är så här långt vi kommit i denna undersökning. Tillsammans med andra kommentarer tyder det alltså på att det är - av rena måloptimeringskäl - bättre att se de sista minuterna i en match/halvlek än att inte göra det.
En annan sak. Som Chadie påpekar i sin kommentar är det inte bara målen som räknas. "Bra fotboll" är - för kännare i alla fall - mer än så. Låt mig då formulera om (eller snarare komplettera frågan).
Låt oss först anta att man är överens om vad "bra fotboll" innebär, dvs att alla begrepp är definierade. Frågan blir då: Om man vill se "bra fotboll" - under den överenskomna definitionen - och har en begränsad tid till detta (säg 2 * 15 minuter) - vilka matchminuter ska man slå på TV:n och titta?
I och för sig kommer jag att se hela Sverige-matchen ikväll (fredagen 2004-06-18), men som uppgifterna ovan antyder kanske det skulle räcka med de sista 15-20 minuterna i respektive halvlek. I alla fall för varannan match.
Posted by hakank at 07:31 EM Posted to Statistik/data-analys | Comments (6)
maj 30, 2004
Kluster i den svenska bloggosfären
David Pettersson på Månhus Beta gör i Kartläggning en intressant kartläggning (klustring) av ett flertal svenska bloggar, som han skriver: efter hur jag uppfattar deras stil, innehåll och hur de håller ihop sinsemellan. Vad jag förstår har han använt sin intuition och inte "hård data" för detta.
Efter att ha skrivit en kort kommentar hos David kom jag på att hans Efter ett snabbt försök att skissa det på papper insåg jag att det är väldigt svårt när man inte har tillgång till åtminstone fem dimensioner. torde innebära att han har fem mer eller mindre uttryckliga dimensioner i åtanke.
Om man kunde få honom att skriva ner, t.ex. i distansmatrisform, vilka bloggar som är lika/långt i från varandra med avseende på de respektive (eventuellt namnlösa) dimensionerna, borde man kunna göra en automatisk klustring, t.ex. via statistik/dataanalys-paketet R som har en hel del metoder för att visa kluster.
För övrigt noterar jag att det finns två stora grupper utan inbördes koppling, fast det är kanske det som David inte riktigt tycker stämmer, eftersom han vill knyta ihop vänster och höger sida. En torus kanske?
Posted by hakank at 10:19 EM Posted to Blogging | Statistik/data-analys | Comments (3)
april 13, 2004
Senaste Chance News
Den senaste (13.03) Chance News har kommit. Se Chance News (och sajt) för mer info om denna sajt.
I detta nummer kan vi bl.a. läsa följande:
- Fördelning av tal i Google
En analys av om tal via google följer Benfords lag, dvs att 1 är betydligt vanligare än 2 som är vanligare än 3 etc. (Jämför gärna med Talfördelning på google - varför är det så ont om 52?.) - Om representative samples (representativt urval)
- Hot teams/hot hands i spel
Artikeln som refereras är Colin Camerer Does the basketball market believe in the 'hot hand'? (PDF). Se även andra dokument på kurs-sajten Finance, Behavioral Economics, and Sports Betting.Där finns f.ö. även den klassiska The Hot Hand in Basketball: On the misperception of Random Sequences (PDF) av Thomas Gilovich, Albert Vallone och Amos Tversky. De först- resp. sistnämnda har skrivits om tidigare, se Kognitiva illusioner.
- Diskussion om risker
- Och som vanligt en kommentar om Marilyn vos Savant har rätt eller inte i sin spalt "Ask Marilyn".
Se även arkivet av äldre nummer. Det finns en announce-mailinglista att prenumerera på.
Posted by hakank at 09:02 FM Posted to Kognitiva illusioner | Statistik/data-analys
april 06, 2004
Mapping Knowledge Domains
Pressreleasen Here there be data: Mapping the landscape of science berättar om forskning kring hur man visualiserar vetenskaper och dess tidskrifter.
The April 6, 2004, issue of the Proceedings of the National Academy of Sciences (PNAS) features nearly 20 articles by some of tomorrow's mapmakers. Representing the computer, information and cognitive sciences, mathematics, geography, psychology and other fields, these researchers present attempts to create maps of science from the ever-growing and constantly evolving ocean of digital data.
"Science is specializing at high speed, which leads to increasing fragmentation and reinvention," said Katy Börner of Indiana University. "Maps of publication databases or other data sources can help show how scientists and scientific results are interconnected."
...
Several of the papers describe ways to analyze article collections and map out landscapes that humans can view. Some methods, such as that proposed by Simon Dennis, "read" scientific articles and use a deep understanding of the content as the basis for a map. Other methods use relationship networks between the articles, such as citation of other papers, as the basis for a map.
Här finns lite större versioner av bilderna (rätt stora är de).
Många av papren verkar spännande och finns online på PNAS Online. En fullständig lista över de aktuella artiklarna: Mapping Knowledge Domains. (Jag tror inte att det kräver någon registrering, i så fall så är det kostnadsfritt).
Ett litet urval:
Jonathan Aizen , Daniel Huttenlocher, Jon Kleinberg, Antal Novak: Traffic-based feedback on the web
Mark Newman: Coauthorship networks and patterns of scientific collaboration.
Via EurekAlert!.
Posted by hakank at 09:17 EM Posted to Statistik/data-analys
mars 31, 2004
Newsmap
Newsmap är ett nyhetsvisualiseringssystem som använder sig av Treemaps-tekniken.
Se vidare
Peter Merholtz (peterme.com): All the pretty colors...
Via peterme.com.
Posted by hakank at 11:02 FM Posted to Statistik/data-analys | Comments (2)
mars 29, 2004
Statistisk data snooping - att leta efter sammanträffanden
Denna anteckning beskriver och ger lite exempel på data snooping - "datasnokning". Efter en inledande begreppsutredning beskrivs ett par tekniska papers, varefter det blir mer lite mer lättsmält material, inklusive ett program att själv leka med.
Data snooping vs annat
"Data snooping" används för att beteckna olika typer av företeelser. Det finns en betydelse som refererar till en form av dataintrång där någon otillbörligt försöker att få reda på andra användares data; det är verkligen inte denna betydelse som avses här.
En något subtilare betydelseskillnad är till data mining. Data mining är explorativ ("datagrävande") till sin natur, men har metoder anpassade för att avgöra om t.ex. ett beslutsträd eller artificiellt neuralt nätverk verkar att ge lovande resultat.
Data snooping är - å andra sidan - den mer tvivelaktiga metoden att först leta reda på intressanta samband i en datamängd för att t.ex. sedan skriva en vetenskaplig rapport med "statistiska förtecken" som om denna inledande grävning inte gjorts. Problemet med data snooping är att detta letande gör att de traditionella statistiska analyserna, t.ex. signifikansvärde, inte längre gäller.
Super Bowl
Patric Burns Permuting Super Bowl Theory (PDF) analyserar den populära teorin att det finns en koppling mellan utgången av den amerikanska högtiden Super Bowl (amerikansk fotboll, alltså) och börsen.
Abstract:
The quality of stock market predictions based on the winner of the Super Bowl is examined using permutation tests. These tests are very easy to perform in modern computing environments like the R language. One key point that comes to light is that the success rate of a prediction is not a good measure of its usefulness. Statistically signi cant success in prediction does not automatically lead to economically profitable strategies.
På R for the Super Bowl finns R-kod (R som i www.r-project.org) för att själv köra exemplen.
Ovanstående paper refererar till två mycket tekniska papers skrivna av bl.a.
Halbert White:
Halbert White: A reality check for data snooping (PDF, ~6Mb)
R. Sullivan, A. Timmermann, and H. White: Data Snooping, Technical Trading Rule Performance, and the Bootstrap (PDF, ~6Mb)
(Av sanningivrande skäl bör noteras att dessa två papers endast har bläddrats i.)
Fler skrifter
Timothy Falcon Crack A Classic Case of "Data Snooping" for Classroom Discussion (PDF)
Abstract:
Data snooping (mistaking spurious statistical relationships for genuine ones) is an important and dangerous by-product of financial analysis. However, data snooping is a difficult concept to explain to students of financial economics because, by its very nature, it is difficult to illustrate by example (a strong statistical relationship between complex financial variables is difficult to refute). To overcome this pedagogical difficulty, I present an example of data snooping where one variable is non-financial: I show that near both new moon and full moon, stock market volatility is higher and stock market returns are lower than away from the new or full moon. The simple and off-beat nature of this example enables substantial classroom discussion.
David Jensen Data Snooping, Dredging and Fishing: The Dark Side of Data Mining, SIGKDD 1999.
Beskriver en paneldiskussion hållen 1999 om data snooping-liknande problem inom data mining. I sista avsnittet föreslås några lösningar på dessa problem.
Mer lättillgängliga skrifter
Så kommer vi till några mer lättillgängliga skrifter.
Bibelkoden
I David Jensens paper nämns som ett exempel på data snooping den teknik som används i bibelkoden (Bible codes) för att "hitta" dolda religiösa "budskap" i Bibeln. Denna teknik kan dock användas för att "hitta" vad som helst i vilken skrift som helst, t.ex. Tolstoys Krig och Fred, Moby Dick eller Microsofts licensöverenskommelse.
För mer i detta ämne se Scientific Refutation of the Bible Codes skriven bl.a. av Brendan McKay samt Skeptical Inquirer-artikeln Hidden Messages and The Bible Code. Sajten Are there Mathematical Miracles in the Qur'an or the Bible? har en omfångsrik samling av liknande forskningar.
Man kan också notera (som tidigare gjorts) att ordet hakank finns i π (pi).
666 och programmet Devil's word
I David A. Gershaw: Is It Just a Coincidence? står bland annat:
Another example [of using coincidences to prove a point] is using any combination of the number "666" to indicate that someone is the Beast of Revelation. Some said that our ex-president, Ronald Wilson Reagan, was the Beast. Why? Each of his names has six letters, therefore "666". However, if you look long enough, you can probably find some arrangement of 666 with almost anyone.
1996 skrev Matthew Hunt och Masto Christopher i Usenet-gruppen comp.lang.perl två Perl-program (antichrist.pl) som gör just detta. Källkoden samt några exempel finns här . Programmet tar ASCII-värdet av en sträng och söker efter en kombination av additioner och subtraktioner över dessa tal för att få fram talet 666, vilket lyckas för många strängar. Många ord har flera kombinationer som uppfyller villkoret, men programmet visar endast den första.
Det finns en nyskriven och webbanpassad version av programmet: Devil's word. För tillfället finns en stygg maxgräns på 20 tecken, som eventuellt senare kommer att justeras.
Exempel på en sådan körning på namnet håkan kjellerstrand:
Checking 'håkan kjellerstrand'....
Character ASCII value
h 104
å 229
k 107
a 97
n 110
32
k 107
j 106
e 101
l 108
l 108
e 101
r 114
s 115
t 116
r 114
a 97
n 110
d 100
+104+229+107+97+110-32+107-106+101+108-108+101-114-115-116-114+97+110+100 = 666
Coincidence? I think not!
Se även
Of birthdays and clusters och The extreme value fallacy från Number Watch som båda behandlar olika typer av data snooping. Dessa samt några andra artiklar kommenteras i blogganteckningen Matematiska och statistiska "självklarheter".
Uppdatering
En uppdaterad version av programmet beskrivs i Uppdatering: Devils' word (sammanträffanden i ord).
Posted by hakank at 10:32 FM Posted to Sammanträffanden | Statistik/data-analys | Comments (2)
mars 21, 2004
Fylogenetiska träd
I veckans Vetenskapsradion (cirka 21:46 minuter in i programmet) har Per Helgesson en krönika om likheter mellan biologisk evolution och språklig evolution, och den nytta forskare inom de olika fälten kan ha av varandra.
Tack Peter Lindberg för påminnelse och pek till programmet. Peter skrev tidigare idag Using Evolutionary Ideas in Linguistics som troligen var inspirerad av samma program.
Både i programmet och i Peters anteckning nämns forskaren Russell Gray som analyserat de indoeuropeiska språkens utveckling och byggt upp släktschema för dessa språk.
Lite mer om Russell Gray finns här:
Russell Current Research Projects
Publications.
På sidan Russell Gray's Data finns datafiler från Russell Gray och Quentin Atkinson Language-tree divergence times support the Anatolian theory of Indo-European origins (PDF).
Fylogenetiska träd
De släktschema, evolutionära träd, som Gray använt kallas för fylogenetiska träd (phylogenetic trees). Jag kikade lite på dessa för några år sedan och samlade en del referenser varav några presenteras nedan.
Bakgrund till intresset
För en liten bakgrund: Intresset triggades troligen av en analys av kedjebrev (Charles Bennett, Ming Li, Bin Ma: Linking Chain Home Page) och som senare skrevs om i Kedjebrevsanalys. Det gjorde mig f.ö. även intresserad av det vidare området computational biology.
Till detta kom en gammal fascination av metriker för att mäta avstånd i datamängder. Se t.ex. Lord of the Strings som beskriver ett försök att mäta vilket naturligt språk som är närmast Tolkiens uppfunna språk.
Sajter och dokument
Här är några av de sajter och texter som då hittades. Den som har tips på nyare och bättre introduktionstexter i detta ämne får gärna höra av sig.
Phylogeny and Reconstructing Phylogenetic Trees med en Java Applet samt kod.
Phylogeny (PDF), från kursen Introduction to Computational Molecular Biology and Genomics.
Susan Holmes Phylogenesis - An overview (ps-fil). Holmes har nämnts tidigare i andra sammanhang, se t.ex. Diaconis om myntsingling, Redan de gamla grekerna höll på med kombinatorik samt Brian Arthur: Lock-in och El Farol.
The Tree of Life Web Project A collaborative Internet project containing information about phylogeny and biodiversity.
Icke-biologiska tillämpningar
Egentligen är jag inte så intresserad av ren biologisk data utan analys av annan data, t.ex. texter såsom kedjebrev och andra artefakter som snarare tillhör memetiken.
Phylogenetic methods for evolutionary economics
New methods of editing, exploring, and reading The Canterbury Tales
Länkar till fler icke-biologiska skrifter som använder liknande metoder finns på Phylogenetics Everywhere
Program
Det finns naturligtvis en mängd program för att analysera och simulera sådana träd. Några som har tittats på:
Statistiksystemet R har paket för manipulation av sådana träd. Se paketlistan (obs stor fil!) och sök på "phylogenetic".
PHYLIP, PHYLogeny Inference Package med dess dokumentation och exempel.
Slutnot
Dessa fylogenetiska träd har länge legat i bakhuvudet och inte en gång utan flera gånger de senaste månaderna har de dykt upp, t.ex. att försöka skapa träd för att visa hur olika nyheter på webben/bloggarna utvecklas (jämför med Hur nyheter sprids på Internet), eller visa "släktskapen" mellan de svenska bloggarna genom att titta på länkar och vilka nyheter som citeras mellan dem.
Posted by hakank at 09:15 EM Posted to Memetik | Statistik/data-analys | Comments (4)
mars 19, 2004
Lord Of The Strings
I de två artiklarna Lord Of The Strings Part 1 och Lord Of The Strings Part 2 görs en analys av vilket naturligt språk som är närmast Tolkiens uppfunna språk. Databasfrågor och programkod medföljer artiklarna.
As a developer, I was thinking about an algorithmic approach to the problem. My idea was to write a program that takes each Tolkien word in turn and finds which real language has the word which is most similar. By inspecting the number of times each language is chosen, we should be able to decide which language was Tolkien’s biggest influence. Of course I would need to look on the Web to find lists of Tolkien words, as well as word lists for other languages, but I assumed that wouldn’t be a problem. My own string similarity metric could be used for the word-by-word comparison, and is a good choice because it acknowledges similarity for a common substring of any size, and is robust to differences in string size. Of course this would be a comparison of lexical similarity, as my string similarity algorithm makes only lexical comparisons. It is still possible that the inspiration for the grammar and the lexical structure of Tolkien’s languages came from entirely different sources.
...
Conclusions
When I started this investigation, I had no idea what the result would be. I just clung firmly onto the belief that my string similarity metric, together with a simple algorithm to iterate over the set of possible word pair comparisons, would provide an interesting result. In fact, the results are very satisfying. I found that English had a profound effect on Tolkien's invented languages, with perhaps further influences from Hungarian and Spanish. This is satisfying because it is entirely reasonable (at least the part about English!), though not exactly what I expected after reading about the (apparently unfounded) claims for the influences of Finnish. It is also satisfying because it increases my confidence in the string similarity method. And as developers, we like to have confidence in our methods.
Se även samme författares (Simon White) Matching Strings and Algorithms.
(Tack Ulf!)
Posted by hakank at 01:13 FM Posted to Statistik/data-analys
februari 25, 2004
Diaconis om myntsingling
Flipping a coin may not be the fairest way to settle disputes. About a decade ago, statistician Persi Diaconis started to wonder if the outcome of a coin flip really is just a matter of chance. He had Harvard University engineers build him a mechanical coin flipper. Diaconis, now at Stanford University, found that if a coin is launched exactly the same way, it lands exactly the same way.
...
But using high speed cameras and equations, Diaconis and colleagues have now found that even though humans are largely unpredictable coin flippers, there's still a bias built in: If a coin starts out heads, it ends up heads when caught more often than it does tails.
Ett cirka 7 minuters reportage med Diaconis finns att belyssna på sajten.
Se även
Persi Diaconis
Susan Holmes
Posted by hakank at 01:17 FM Posted to Statistik/data-analys | Comments (2)
januari 21, 2004
Senaste R News (3/2003)
Senaste (nr 3/2003, PDF) R News (för statistik- och dataanalyssystemet R) innehåller bland annat följande artiklar:
* R as a Simulation Platform in Ecological Modelling
Intressant artikel som diskuterar olika typer av simuleringar såsom (från rubrikerna): Differential equations, Individual-based models, Individual-based population dynamics, Particle diffusion models, Cellular automata
Se även Thomas Petzoldt's Tutorials, Tools and Downloads. Det finns lite demoprogram här (några är i stort sett identiska med artikelns exempel).
* Dimensional Reduction for Data Mapping
Diskuterar och visar exempel på olika metoder såsom: Principal component analysis, Multi-dimensional scaling, The self organising map, Independent component analysis and projection pursuit,
* Debugging Without (Too Many) Tears
Posted by hakank at 01:43 EM Posted to Statistik/data-analys
december 19, 2003
Automatisk identifikation av språk (språkidentifiering)
Mats Andersson frågar hur man identifierar ett visst språk.
Tyvärr fungerar det inte så bra att bara titta på fördelningen av enskilda bokstäver (som Mats antyder som en lösning), utan man arbetar ofta med n-gram, dvs "löpande" n-boktavsdelar av texten. (Exempel: 2-gram (bigram) på ordet "mats" är "ma", "at", "ts".) Efter att ha analyserat en stor mängd dokument på olika språk arbetar man vidare med tekniker som beskrivs via nedanstående länkar.
[F.ö. är det n-gram jag använder i mina markov-program för att generera ord eller texter, t.ex. New Markov words II, skapa svenska ordstäv, Bob Hund texter, etc. Om det nu förklarar något. :-)]
Exempel:
Gå till Unknown Language Identification och skriv in en text, t.ex. den där Mats skriver sin fråga. Förklaringen av hur programmet fungerar finns på The Acquaintance Algorithm.
Här är några andra länkar om automatisk språkigenkänning (språkidentifiering, language identification):
TextCat, som också har kod skriven i Perl.
Det finns en bibliografi t.ex. på Automatic Language Identification Bibliography. Tyvärr är rätt många länkar obsoleta.
En massa andra språkidentifieringsredskap finns på Language Identification Tools. Där finns även pekare och referenser.
Fagan Finder har samlat en hel del av dessa som man kan testa, men det funkar tydligen inte nu. Däremot fungerar många av de sajter som finns på sidan, så klicka vidare.
Mer finns via google: "language identification".
Ett annat skoj område är automatisk textsammanfattning (text summarization). Se t.ex.
SweSum - Automatisk Textsammanfattare av
Vad är automatisk textsammanfattning?
Textsammanfattning
The Text Summarization Project
Text Summarization
Se även den alltid inspirerande Viggos språktekniksida (Viggo Kann)
Posted by hakank at 01:33 EM Posted to Språk | Statistik/data-analys
november 22, 2003
Senaste R-versionen: 1.8.1
Senaste versionen av R, 1.8.1, släpptes i går. Ladda ner filen R-1.8.1.tgz, vilket är en tar gz-fil med källkod. Se denna sida för binärer till olika operativsystem. Läs nyheterna i den senaste versionen (märkligt nog används https).
För intresserade av R kan jag även rekommendera mailingliste-arkiven, främst för r-announce och r-help.
Posted by hakank at 10:53 FM Posted to Statistik/data-analys
november 21, 2003
Talfördelning på google - varför är det så ont om 52?
Jonas Söderström är fascinerad av talet 47. Jag blev nyfiken på hur ofta talet 47 egentligen förekommer, och gjorde därför en liten undersökning hur talen 0 till 100 google-fördelas, dvs antal träffar på google för respektive tal (per 21 november 2003).
Det visar sig att talet 47 kommer på 54 plats precis efter talet 23. De ovanligaste talen var 52 och 77. I och för sig kan det vara så att talet 47 är kopplat till de viktiga sakerna och fenomenen i tillvaron, det säger förevarande undersökningen ingenting om.
Läs vidare och se de sensationella bilderna i Talfördelning på google!
Uppdatering
Peter Lindberg tipsade mig om två sajter med mycket mer data än mina ynka 101 tal.
The Numbers that Shape our World av Olof Runborg som i september 2000 studerade talen 11 till 1000. Där finns också en referens till Benford's Law. [Åtminstone en av länkarna på Benford-lagens sida är obsolet. Följande länk fungerar i skrivande stund: The Power of One av Robert Matthews, en av mina favoriter.]
The Secret Lives of Numbers har en mycket fräck interaktiv visualisering. Zooma in i ett intervall genom klicka i grafen. Man skriver så här:
Since 1997, we have collected at intervals a novel set of data on the popularity of numbers: by performing a massive automated Internet search on each of the integers from 0 to 1,000,000 and counting the number of pages which contained each, we have obtained a picture of the Internet community's numeric interests and inclinations.
Jag kan också rekommendera ett besök hos Golan Levin som är en av dem bakom ovanstående projekt. Där finns fler visualiseringar och skojiga projekt.
Posted by hakank at 08:51 EM Posted to Statistik/data-analys | Comments (2)
oktober 30, 2003
Senaste R News
R News är ett nyhetsbrev för systemet R som jag har skrivit om/i några gånger här på bloggen. (Senast var det i De svenska myntens talsystem.)
Det senaste (PDF) numret innehåller bland annat följande:
- R Help Desk: An Introduction to Using R s Base Graphics
- Integrating grid Graphics Output with Base Graphics Output
- A New Package for the General Error Distribution
- Web-based Microarray Analysis using Bioconductor
- Book Reviews
- samt lite nyheter om den senaste versionen och senaste paketen på CRAN (utbruten ur framesystemet, stor fil!).
Posted by hakank at 09:41 FM Posted to Statistik/data-analys
oktober 23, 2003
Sista Chance News
Sista Chance News? Ja, det är tyvärr rätt. Efter 12 års trogen tjänst diskontinueras denna underbara skrift. Det är tråkigt eftersom det alltid fanns några guldklimpar som var lärorika och underhållande.
I stället publicerar man Current chance news articles, där det nog inte kommer att vara lika bearbetade artiklar som i Chance News. Borde tipsa dem om att göra det till en blogg, med RSS-flöde (-förs) och allt.
Det sista numret finns som HTML eller PDF.
Glöm inte att man kan söka i äldre artiklar nederst på första sidan.
Posted by hakank at 08:42 EM Posted to Statistik/data-analys
oktober 15, 2003
Simulering av sammanträffanden - I
När jag häromdagen läste Persi Diaconis och Frederick Mostellers underbara paper "Methods for Studying Coincidences" skrev jag lite R-kod för att testa vissa avsnitt. Några exempel publicerades i blogganteckningen Sammanträffanden - anteckningar vid läsning av Diaconis och Mosteller 'Methods for Studying Coincidences'.
Dock skrev jag då ingen simulering av hur sammanträffanden slumpmässigt kan uppstå, vilket nu åtgärdas i Simulering av sammanträffanden - I .
Varning: dokumentet kan upplevas som tekniskt av känsliga personer.:-)
Mer om R, systemet som använts, finns på www.r-project.org.
Posted by hakank at 10:10 EM Posted to Sammanträffanden | Statistik/data-analys
oktober 09, 2003
DM Review-artikelserien om sociala/komplexa nätverk är nu komplett
Som jag skrev i DM Review-artikel om sociala/komplexa nätverk har DMReview en artikelserie i tre delar om analys av sociala/kompexa nätverk. Samtliga delar är nu publicerade:
Se även Expanded References.
Några andra intressanta artiklar från senaste numret är:
Finding the Needle in the Haystack: Using Data Visualization to Spot Patterns and Anomalies in Business Data
Data Mining and Modeling: The Bayesian Debate.
Posted by hakank at 09:11 EM Posted to Statistik/data-analys
oktober 05, 2003
Sammanträffanden - anteckningar vid läsning av Diaconis och Mosteller 'Methods for Studying Coincidences'
[Om denna anteckning är svårläst på huvudsidan, försök då att läsa det som separat anteckning här]Detta är en liten anteckning med anledning av papret Methods for Studying Coincidences av Persi Diaconis och Frederick Mosteller som jag lyckades få tag i tack vare en snäll person. Tack!
Studiet av coincidences (sammanträffanden) är relaterat till kognitiva illusioner som jag (egentligen) håller på att kolla in. Vi har dålig intuition om sammanträffanden, vilket födelsedagsproblemet visar: Födelsedagsproblemet säger att det krävs 23 personer för att det ska vara 50% chans att två av personerna i denna grupp har samma födelsedag. Förvånande? En vanlig intuition är att det krävs många fler personer.
Se nedan för refererenser om detta mycket berömda problem.
Här nedan går jag igenom ett av de intressantaste avsnitten i Diaconis och Mostellers paper, avsnittet "7.1 General-Purpose Models: Birthday Problems" (sid 857ff).
Mestadels består denna anteckning av citat från papret och en del R-kod. Statistik/data analys-paketet R finns att ladda ner på www.r-project.org.
I övrigt finns det andra mycket intressanta diskussioner i artikeln, t.ex.
- sannolikheten att man, efter ha lärt sig ett nytt ord, "inom kort" stöter på det igen.
- B.F. Skinners analys om Shakespeares alliterationer. Skrev han verkligen så många och så medvetet som vi (tydligen) antagit?
- diskussioner relaterade till ESP-forskning.
The Standard Birthday Problem
Detta är standardversionen av födelsedagsproblemet.
Problem 1: The Standard Birthday Problem. Suppose N balls are dropped at random into c categories, N <= c. The chance of no match (no more than one ball) in any of the categories is
prod(1-i/c, i=1..N-1) (Expression 7.1)
... If c is large and N i small compared to c**(2/3), the following approximation is useful. The chance of no match is approximately
exp(-N**2/2*c) (Expression 7.2)
This follows easily from Expression (7.1), using the approximation
log_e(1-i/c) ~ -i/c
To have probability about p of least one match, equate (7.2) to 1-p and solve for N. This gives the approximations
N ~ 1.2 * sqrt(c) (Expression 7.3)
for a 50% chance of match and
N ~ 2.5 * sqrt(c)
for a 95% chance of match.
[...]
Thus, if c=365, N=22.9 or 23 for a 50% chance and about 48 for a 95% chance.
I R skriver man:
> 1.2 * sqrt(365) [1] 22.92597 > 2.5 * sqrt(365) [1] 47.76243Many Types of Categories
Följande problem är mycket intressant. Här räknar man (approximativt) ut hur stor sannolikheten är för att det finns sammanträffande där det finns flera attribut. I standardversionen av födelsedagsproblemet är det ju endast ett attribut (samma födelsedag). Här generaliseras alltså detta.
Problem 2: Many Types of Categories.
...
Suppose that a group of people meet and get to know each other. Various types of coincidences can occur. These include same birthday; same job; attended same school (in same years); born or grew up in same country, state or city; same first (last) name; spouses' (or parents') first names the same; and same hobby. What is the chance of a coincidence of some sort?
....
If the numbers of [independent] categories in the sets are c1, c2,...ck, we can compute the chance of no match in any of the categories and subtract from 1 as before. If k different sets of categories are being considered, the number of people needed to have an even chance of a match in some set is about
N ~ 1.2 * sqrt(1/ (1/c1 + 1/c2 + ... 1/ck)
The expression under the square root is the harmonic mean of the ci divided by k. If alla ci equal c, the number of people needed becomes 1.2*(c/k)^1/2 so that multiple categories allow coincidences with fewer people as would be expected. For a 95% chance of at least one match, the multiplier 1.2 is increased to 2.5 as in Expression 7.4.
...
As an illustration, consider three categories: c1 = 365 birthdays; c2= 1000 lottery tickets; c3 = 500 same theater tickets on different nights. It takes 16 people to have an even chance of a match here.
I R:
För en 50-50-chans för en match kräver alltså 16 personer:
> 1.2 * sqrt(1/sum(1/c(365,1000,500))); round(.Last.value) [1] 15.83929 [1] 16Och för 95% chans till en match krävs 33 personer:
> 2.5 * sqrt(1/sum(1/c(365,1000,500))); round(.Last.value) [1] 32.99852 [1] 33Multiple Events
Här studeras en match för k antal personer som ska ha samma attribut (t.ex. samma födelsedag).
Problem 3. Multiple Events. With many people in a group it becomes likelu to have triple matches or more. What is the least number of people required to ensure that the probabilit exceeds 1/2 that k or more of them have the same birthday? McKinney (1966) found, for k=3, that 88 people are required. For k=4, we require 187.
....
The number of people required to have the probability of p of k or more in the same category is approximately [...]
N*E**(-N/(c*k)) / (1 - N/(c*(k+1)))^(1/k) =
( c**(k-1) * k! * log_e(1/(1-p)) )**(1/k) (Expression 7.5]
....
[Example:]
A friend reports that she, her husband, and their daughter were all born on the 16th. Take c = 30 (as days in a month), k = 3, and p = 1/2. Formula (7.5) gives N ~ 18. Thus, among birthdays of 18 people, a triple match in day of the month has about a 50-50 chance.
R-kod:
Först lite förklaringar:
log är logaritmen med basen E.
Funktionen factorial() finns i paketet gregmisc och är definierad som
factorial <- function(x) { gamma( 1 + x)}
Det kan även skrivas som prod(1:k), dvs
> c=30; k=3; p=1/2; (c**(k-1) * prod(1:k) * log(1/(1-p)) )**(1/k) [1] 15.52648men om man vill arbeta med vektorer, t.ex. testa för olika värden av k (t.ex. 1:10), blir det problem att ha ytterligare en vektor i prod(1:k)
> c=30; k=3; p=1/2; (c**(k-1) * factorial(k) * log(1/(1-p)) )**(1/k) [1] 15.52648Trist! Jag förväntade mig värdet (ungefär) 18 här.
Jag pushar ovanstående diskussion och kollar in detta problem lite mer.
Funktionen qbirthday finns som standard i R som är följande (via hjälpen, ?qbirthday):
Computes approximate answers to a generalised ``birthday paradox'' problem. `pbirthday' computes the probability of a coincidence and `qbirthday' computes the number of observations needed to have a specified probability of coincidence.
Man refererar explicit och endast till Diaconis och Mostellers paper.
Är det fel i papret?
Med min formel får jag princip samma som följande:
> qbirthday(prob=0.5, classes=30, coincident=3) [1] 16Jag jämför här min formel med qbirthday för olika k-värden, och avrundar sålunda till heltal.
> c=30; k=1:10; p=1/2; round((c**(k-1) * factorial(k) * log(1/(1-p)) )**(1/k)) [1] 1 6 16 26 37 48 59 71 82 93 > c=30; k=1:10; p=1/2; sapply(k, function(i) qbirthday(prob=p, classes=c, coincident=i)) [1] 1 6 16 26 37 48 59 71 82 93De ser ut att vara identiska! Jag vet tyvärr inte varför våra värden skiljer sig mot papret.
Tyvärr hittade jag även följande problem: För stora värden av k (t.ex. 1000) är min formel dålig eftersom den ger Inf (infinity) i factorial(). Även om man i stället använder prod(1:k) blir det Inf. Efter lite undersökningar visar det sig att max-värdet för k är 170. Så qbirthday är att föredra i sådana fall.
> c=30; k=1000; p=1/2; round((c**(k-1) * factorial(k) * log(1/(1-p)) )**(1/k)) [1] Infmedan qbirthday inte har några problem med stora värden för k (t.ex. 1000):
> c=30; k=1000; p=1/2; sapply(k, function(i) qbirthday(prob=p, classes=c, coincident=i)) [1] 11043OK. Nu vet vi det.!
Så, tillbaka till huvudspåret.
För en simulering av födelsedagsproblemet med k = 3 resp. 4 får vi följande approximationer (jämför med svaren 88 resp 187 som nämns ovan). Vi jämför också med qbirthday för att kolla.
> c=365; k=3; p=1/2; (c**(k-1) * factorial(k) * log(1/(1-p)) )**(1/k) [1] 82.13359 > qbirthday(prob=0.5, classes=365, coincident=3) [1] 82 > c=365; k=4; p=1/2; (c**(k-1) * factorial(k) * log(1/(1-p)) )**(1/k) [1] 168.6471 > qbirthday(prob=0.5, classes=365, coincident=4) [1] 169Dvs det krävs (approximativt enligt "vår" metod) 83 personer för att, med 50% chans, tre eller flera personer ska ha samma födelsedagar.
Almost Birthdays
Detta är vad författarna även kallar för multiple endpoints, dvs att två saker nästan matchar. Tillåter vi sådana nästan-matchningar (och ofta görs det utan någon uttrycklig gräns för var "nästan" slutar) blir sannolikheten hög för en träff.
Problem 4: Almost Birthdays.
...
How many people are needed to make it even odds that two have a birthday within a day.
...
A neat approximation for the minimum number of people required to get a 50-50 chance that two have a match within k, when c categories are considered [...] is approximately
N ~ 1.2 * sqrt(c/(2*k + 1) (Expression 7.6)
When c = 365 and k = 1, this approximation gives about 13 people (actually 13.2).
I R:
> 1.2 * sqrt(365/(2*1 + 1)) [1] 13.23631Om vi kollar denna approximering från 0 dagar till 20 får vi följande:
> sapply(0:10, function(i) round(1.2 * sqrt(365/(i*1 + 1)),1)) [1] 22.9 16.2 13.2 11.5 10.3 9.4 8.7 8.1 7.6 7.2 6.9dvs det krävs ungefär 7 personer för att det ska vara 50% chans att två personer fyller år inom 10 dagars räckvidd.
Jag antar nu (men det står inte uttryckligen i papret) att detta gäller samma som tidigare, dvs vi multiplicerar med 2.5 för att få 95% chans till en match. Vi får då:
> sapply(0:10, function(i) round(2.5 * sqrt(365/(i*1 + 1)),1)) [1] 47.8 33.8 27.6 23.9 21.4 19.5 18.1 16.9 15.9 15.1 14.4dvs med 15 personer är vi tämligen säkra (95%) att det finns två födelsedagar inom 10 dagars räckvidd.
The Law of Truly Large Numbers Slutligen avslutas med följande tänkvärda (och möjligen i efterhand självklara) citat:
The Law of Truly Large Numbers.
Succinctly put, the law of truly large numbers states: With a large enough sample, any outrageous thing is likely to happen. The point is that truly rare events, say events that occur only once in a million [as the mathematician Littlewoood (1953) required for an event to be surprising] are bound to be plentiful in a population of 250 million people. If a coincidence occurs to one person in a million each day, then we expect 250 occurences a day and close to 100000 such occurences a year.
Going from year to a lifetime and from the population of the United States to that of the world (5 billion at this writing), we can be absolutely sure that we will see incredibly remarkable events. When such events occur, they are often noted and recorded. If they happen to us or someone we know, it is hard to escape that spooly feeling.
Se även följande om födelsedagsproblemet
Birthday Problem
Coincident Birthdays
Coincidence
The Skeptic's Dictionary: law of truly large numbers (coincidences)
Relevanta tidigare blogganteckningar (och referenser):
Tankeillusioner och tankemisstag
Chance News (och sajt)
Att förutsäga framtiden i efterhand - hindsight bias/creeping determinism (läs även kommentarerna).
Uppdatering
Mer om simulering av sammanträffanden finns i Simulering av sammanträffanden - I.
Posted by hakank at 09:39 EM Posted to Sammanträffanden | Statistik/data-analys
september 30, 2003
Statistikknarkande: Antal webb-besökare och power law
Av lite olika anledningar har jag nu kollat in hur många unika besökare jag haft under det exakt (på dagen!) ett år min sajt (www.hakank.org) började notera i webbserverloggen.En unik besökare är här definierad som ett unikt IP-nummer. Ja, det är problem med dynamiska IP-nummer och proxys på större företag. Men så är världen nu beskaffad....
Jag har här räknat med samtliga "besökta filer" som finns i min webbserverlogg, inklusive bilder (det lilla fåtal jag har), RDF- och CSS-filerna till bloggen, class-filerna till Java Applets, etc.
Här är resultatet av undersökningen.
Unika besökare
Det har varit 33876 unika IP-nummer-besök på totalt 150889 besök, dvs varje besökare har gjort i genomsnitt 4.45 besök. Igenomsnitt har det varit cirka 413 besök per dag och cirka 93 unika besökare per dag. (De senaste månaderna har jag dock snittat på cirka 1000 besök per dag.)
De mest frekventa besökarna:
Sök-bottarna dominerar naturligtvis, vilket vi ser i listan över de mest frekventa besökarna. Av totalt 150889 träffar var 27976 sökbott-träffar, dvs cirka 18%, vilket innebär att ungefär var femte besökare är en sökbott (egentligen var 5.5:e)!
Besökare: antal besök
crawler11.googlebot.com: 1806 [en frekvent index.rdf-hämtare]: 1690 crawler10.googlebot.com: 1677 cr031r01-2.sac2.fastsearch.net: 1648 trek18.sv.av.com: 1518 crawler14.googlebot.com: 1468 12.148.209.198: 1158 buildrack17.sv.av.com: 979 cr1.turnitin.com: 972 crawlers.looksmart.com: 814 drone10.sv.av.com: 735 [amerikansk bott, ej sökmotor]: 727 drone6.sv.av.com: 698 [en nära vän]: 678 si1006.inktomisearch.com: 641 crawler12.googlebot.com: 607 ....
Bottar
De 8 större bottar jag kom att tänka på, fördelar sig på följande sätt. Här har jag slagit ihop alla IP-nummer från en domän till en entry:
googlebot.com: 8170 sv.av.com: 7096 inktomisearch.com: 3873 alexa.com: 3061 fastsearch.net: 2928 looksmart.com: 1370 teoma.com: 1296 directhit.com: 182
Frekvenstabell
Här nedan följer ett litet utdrag ur en sammanställning av antal besökare som haft en viss besöksfrekvens. Dvs det finns en dator (googlebot naturligtvis) som besökt min sajt 1806 gånger, en som besökt 1690 gånger osv. Sist har vi engångsbesökarna som är 21886 till antalet. Det är alltså sorterat i antal besök (flest först).
Här är datafilen.
Antal besök: antal besökare 1806: 1 1690: 1 1677: 1 1648: 1 1518: 1 1468: 1 1158: 1 979: 1 972: 1 814: 1 735: 1 727: 1 698: 1 678: 1 641: 1 607: 1 605: 1 576: 1 ..... 14: 92 13: 73 12: 119 11: 120 10: 171 9: 195 8: 273 7: 341 6: 483 5: 641 4: 1193 3: 2290 2: 4873 1: 21886
Power law
Naturligtvis började jag att fundera på hur denna fördelning ser ut i en log-log-graf. Skulle det möjligen vara en power-law-fördelning på antalet besök vs antalet besökare? (Se nedan för referenser till power law.)
Med några raska R-kommandon undersökte jag detta närmre. R finns att ladda ner på www.r-project.org.
> hits<-read.table("hits.dat", header=T, sep=",")
> plot(hits, type="l")
En log-log-plot:
> plot(hits, log="xy")

Tja, det ser faktiskt ut som ett skolexempel på en power law!
För att studera det lite mer statistiskt använder jag funktionen nls() från paketet nls.
> library(nls)
> hits.nls <- nls(hosts ~hits^B, data=hits, start =
c(B=0.1),control=list(maxiter=100),alg="plinear",trace = TRUE)
508371265 : 0.1000 56.2787
498492486 : -0.1094190 368.8806565
451677547 : -0.3347585 1975.0531057
317338776 : -0.588109 6945.458497
144332341 : -0.8947935 13969.2739399
38531928 : -1.295967 18993.358662
4431768 : -1.760797 21213.372275
170968.8 : -2.061232 21792.250830
59470.55 : -2.127369 21872.694076
59302.93 : -2.130101 21875.741431
59302.92 : -2.130125 21875.768037
59302.92 : -2.130125 21875.768235
> hits.nls
Nonlinear regression model
model: hosts ~ hits^B
data: hits
B .lin
-2.130125 21875.768235
residual sum-of-squares: 59302.92
Detta innebär att -2.130125 är koefficienten, dvs
hosts = hits^-2.130125
Värdet 21875.768235 är intercept. Notera dock att vi kommer att använda 10-logartimen av detta värde nedan när vi ritar ut bilden:
> log10(21875.768235 ) [1] 4.339963
Summary:
> summary(hits.nls)
Formula: hosts ~ hits^B
Parameters:
Estimate Std. Error t value Pr(>|t|)
B -2.130e+00 3.367e-03 -632.7 <2e-16 ***
.lin 2.188e+04 1.580e+01 1384.5 <2e-16 ***
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 15.85 on 236 degrees of freedom
Correlation of Parameter Estimates:
B
.lin -0.2368
Här ser vi att både exponenten och intercept är statistiskt signifikanta (p<0.001).
Vi har nu allting som krävs för att rita ut den fullständiga bilden:
> plot(hits, log="xy") > abline(log10(21875.768218), -2.130125, col="red")
Så här blev bilden:
 .
.
Här är den som PDF-fil.
Man ska tolka bilden på följande sätt: Det finns många besökare som gjort ett fåtal besök, och ett fåtal besökare som har gjort många besök. Den räta (regressions-)linjen på en log-log-skala (bas 10) är ett kännetecken på att det är frågan om en power law. Notera att värdena på axlarna inte är log10-värden utan de riktiga "oskalade" värdena. Återigen: Exponenten, lutningen på linjen (log-log skala) är cirka 2.13.
Hur ska vi nu förklara detta? Power law brukar vara ett kännetecken på att det finns någon form av "skiktning" (orättvisa, etc) i befolkningen som studeras. T.ex. Paretos berömda tes att de 20% rikaste äger 80% av världens tillgångar. "De som har ska vara givet". Se även häromdagenanteckningen Segregeringseffekter inom yrken för några fler exempel.
En sak är ju klar, de som besöker sajten flest gånger är maskiner och inte vanliga "manuella" användare (med ett lysande undantag för den nära vännen). Jag kom på att man skulle kunna ta bort värdena för alla bottar och se hur figuren blir då. Men det blir en annan gång...
Några referenser till power-law
Zipf, Power-laws, and Pareto - a ranking tutorial
Power Laws, Weblogs, and Inequality.
Se även mina andra skriverier om detta.
Uppdatering
Flera referenser om power law-fenomenet finns via JonblOGG, anteckningen Power Laws. Det är även i övrigt en intressant blogg.
Artiklar av Jacob Nielsen:
Zipf Curves and Website Popularity
Diversity is Power for Specialized Sites
Do Websites Have Increasing Returns?
Av Jason Kottke: Weblogs and power laws
Samt:
Vilfredo Pareto
The Marginal Productivity Theory of Distribution
Posted by hakank at 03:14 FM Posted to Statistik/data-analys
september 07, 2003
Veckodagsnamn på google - återkomsten
För ett tag sedan gjordes en analys av förekomster av veckodagsnamn på google. Se min anteckning Veckodagsnamn på google för mer om bakgrunden till detta projekt.
Edliga löften gavs att återkomma med en ny sådan när vi fått data från en hel månad. En sådan analys görs i Google veckodagsnamnsanalys 2.
Möjligen, jag skriver möjligen, kommer en ny analys att göras vid något senare tillfälle.
Posted by hakank at 09:34 EM Posted to Statistik/data-analys
augusti 14, 2003
Veckodagsnamn på google
Mats Andersson på Klocklös i Tiden har en hel del roliga funderingar och problem, bland annat att undersöka fördelningen av veckodagsnamn på google. Läs mer om detta på Veckodagsstatistik. Se även det tidigare Veckodagar.
Jag har nu kollat de senaste resultaten med hjälp av statistikpaketet R, och kan inte annat än att hålla med Mats om att det inte verkar finnas några tendenser när man gör dessa sökningar över en vecka. Vi hade en hypotes om "fönster"-effekt (se diskussionerna), men den verkar alltså inte stämma.
Mina ostrukturerade findings, med R-kod, finns på en separat sida, nämligen Veckodagsnamnsanalys.
Se även den liknande diskussionen om fördelningen av månadsnamn:
Populäraste månaderna och Ny månadssökning.
Posted by hakank at 10:02 EM Posted to Statistik/data-analys
augusti 12, 2003
Kort om R och simulering - ett praktikfall
Som utlovat kommer här en liten förklaring till R-koden som finns i Ännu ett verklighetesexempel. Det är två one-liners som simulerar sannolikheten för tärningskast med lite olika förutsättningar.
Målgrupp: Denna anteckning är skriven med Mats i bakhuvudet, men alla "du":n och "man" är generella och riktar sig till alla som är intresserade, inte bara Mats.
Jag kommer här endast att förklara en liten bråkdel vad R kan. Det är mycket kompetent vad gäller statistisk analys, såväl numeriskt som grafiskt.
Först lite kort om R och hur man får reda på mer om systemet. Huvudsidan till systemet är http://www.r-project.org/. Det finns att ladda ner via CRAN (The Comprehensive R Archive Network). Binärer finns för Linux, MacOS och Windows, och skulle man inte vara nöjd med det, finns även källkoden att ladda ner och kompilera själv.
CRAN innehåller även ett stort antal Contributed Packages, av mycket skiftande syfte.
Dokumentation om R, finns via vänstermenyns Documentation. Om du får mersmak för R, rekommenderar jag att man läsa igenom FAQ-dokumentet.
Det finns en liten söksida, där man dels kan söka efter funktioner, dels kan använda den hierarkiska listan för att hitta lämpliga funktioner. Notera att dokumenten som finns via denna även sida kopieras lokalt vid installationen (i alla fall för Linux-versionen). I systemet finns även lite hjälpfunktioner, men av lite olika skäl tenderar jag att använda mitt lilla externa Perl-program för att söka, och som jag gärna lånar ut.
Så, till förklaringen:
Det första exemplet
sum(sapply(1:1000000,function(x)all(sample(1:6,6,replace=T)==1:6)))/1000000
simulerar 1000000 kast med 6 tärningar för att räkna ut sannolikheten att dessa tärningar kommer upp ordnade enligt 1,2,3,4,5,6. Notera att det var inte riktigt det Mats ville ha. Men det är något enklare att förklara, så vi börjar med det.
Vi börjar att förklara inifrån:
sample(1:6, 6, replace=T)
1:6: innebär helt enkelt listan 1,2,3,4,5,6. I R kan det även skrivas c(1,2,3,4,5,6), där c() betyder "combine".
sample är funktionen för att göra ett slumpmässigt urval av elementen i listan. Parametrarna är först listan av möjliga värden (1:6), sedan hur många värden som ska returneras varje gång, (6). Det sista replace=T betyder att det är möjligt att returnera samma värde flera gånger (av de möjliga 6), T står för True. Några exempel på möjliga returvärden: c(1,2,3,4,5,6), c(1,1,1,1,1,1), c(2,1,2,1,2,1) etc. Om man skulle användareplace=F (F=False) innebär det att man inte tillåter upprepningar av elementen, men det är inte vår förutsättning (eftersom tärningarna helt oberoende kommer upp med värdena 1:6).
Nästa steg:
all(sample(1:6,6,replace=T)==1:6)
Här görs två saker. Först kontrolleras om det erhållna värdet från sample() är listan 1:6. Detta returneras en lista av True/False (T/F). T.ex. om listan som returneras från sample() är c(1,2,3,4,3,3) kommer kontrollen mot 1:6 (==1:6) att returnera c(T,T,T,F,F,F). Eftersom vi här endast är intresserade av att alla värdena ska vara True omsluter vi detta med all(), som just kontrollerar om alla värdena är True. Är så inte fallet, som i fallet med c(1,2,3,4,3,3), returneras False.
Nästa steg är att förklara vad sapply() gör.
sapply(1:1000000,function(x)all(sample(1:6,6,replace=T)==1:6)))
sapply() används här för att skapa de 1000000 (en miljon) anrop som krävs för simuleringen. Jag föreslår definitivt att man, när man börja skriva en simulering, startar med betydligt mindre tal, t.ex. 1000, för att se om saker och ting verkar stämma. Och man kan sedan öka detta tal beroende på önkvärd precision, tid och lust.
sapply är en av de funktionella operatorerna som finns i R. Parametrarna är sapply(lista, funktion), där lista är någon form av lista, här listan av talen 1 till 1000000 och är nog inga svårigheter att förstå. Nästa parameter är den funktion som ska köras för varje element i listan.
Som funktion har vi här en "anonym funktion", dvs det är inget anrop till en skriven funktion. Sådana anonyma funktioner måste vara på formen function(parametrar), där parametrar helt enkelt är en lista på de variabler som ska använda i den anropade funktionen. I vårt fall använder vi inga parametrar, dvs vi gör egentligen inte speciellt med talen från listan, utan de används endast för att skapa ett visst antal sample-körningar. Det måste dock finnas åtminstone en parameter till function, vilket jag envetet kallar x.
Så nu har vi alltså en lista med talen 1:1000000 och en anonym funktion all(sample(1:6,6,replace=T)==1:6)), som ska köras för varje element.
Som returvärde ger sapply en lista med värdena från alla anrop som gjorts, dvs den anonyma funktionen applicerad för alla element. Vi får här en lista av True/False beroende på om sample var av korrekt slag eller inte.
Slutligen (!) har vi det fullständiga uttrycket:
sum(sapply(1:1000000,function(x)all(sample(1:6,6,replace=T)==1:6)))/1000000
som gör två saker: Först görs en summering (med sum) på listan som sapply returerar. Notera att detta är en lista med True/False, men sum på en sådan lista räknar helt enkelt hur många True som finns i listan. Dvs sum() ger här antalet sample() som returnerar talen 1:6 i den avsedda ordningen (1,2,3,4,5,6).
Detta tal (som jag fick till 23 i min körning) måste vi sedan dela med antalet körningar (1000000) för att till slut få sannolikheten.
När jag väl insåg vad Mats menade (naturligtvis efter jag publicerade min lösning), att ordningen inte skulle spela någon roll, justerade jag helt enkelt funktionen till följande:
sum(sapply(1:100000, function(x) all(sort(sample(1:6,6, replace=T))==1:6)))/100000
dvs lade endast till sort(). Detta innebär att man man först sorterar listan innan man jämför med 1:6. Annars är det exakt samma som föregående.
Några slutkommentarer:
Dessa kärva one-liners kan skrivas mer strukturerat, men, som jag skrev i inlägget, är jag van att skriva på detta sätt för mindre simuleringar. Mer komplicerade saker måste man hantera något annorlunda, fast det är samma princip. T.ex. skriver man då funktionen som en namngiven funktion i stället för en anonym, men jag vill inte gå in på sådant här.
Har du några frågor om ovanstående eller om R i övrigt, får du gärna höra av dig. Systemet är som sagt mycket kompetent.
Posted by hakank at 09:30 EM Posted to Statistik/data-analys | Comments (1)
augusti 04, 2003
Matematiska och statistiska "självklarheter"
Thomas Schellings bok Micromotives and Macrobehavior handlar om hur beteende på individnivå kan påverka en grupps beteende, vilket i sin tur påverkar individen, vilket i sin tur.... Han ger många exempel på sådana fenomen såsom trafikköer, hur man väljer en plats i en föreläsningslokal, skickar julkort till varandra, hur man grupperar sig på fester etc.
En av de saker Schelling är mest känd för (han har även skrivit betydande verk inom spelteorin) är sin analys av segregering: om samtliga inom en befolkning kan acceptera ett blandat grannskap men kräver att det åtminstone finns minst 30% av grannar av "samma slag", så tenderar det att bli en rätt kraftig segregering. Det är alltså makrobeteende (segregering) som uppstår ur mikromotiv (minst 30% grannar av samma slag). Segregering inom bostadsorter, och grupperingar på fester är några exempel på detta.
Kapitel 2 ('The inescapable mathematics of musical chairs') handlar om vissa grundläggande "självklara" sanningar om aggregerade värden, dvs värden för en hel grupp (medelvärden etc) som man kanske inte så ofta tänker på eller inser vidden av. Schelling listar upp en rad sådana sanningar, t.ex. att det alltid finns någon som är först respektive sist när vi sorterar personer enligt något specifikt kriterium, t.ex. längd, betyg på ett prov eller inkomst. Han drar en hel del slutsatser, t.ex. vad man ska tänka på när man planerar trafikljus eller skidliftar.
[Mer om mikromotiv/makrobeteende och hur de kan simuleras kommer, som tidigare utlovats, inom en framtid.]
När jag läste detta kapitel om matematiska/statistiska "självklarheter" kom jag att tänka på några bra artiklar jag läste för ett tag sedan. De handlar om olika typer av feltänk som är mycket lätta att göra och som vi rätt ofta gör. Artiklarna kan förhoppningsvis öka känsligheten att detektera sådana feltänk.
Of birthdays and clusters. I data över en tillräckligt stor grupp finns det alltid någon typ av kluster att hitta, om man letar tillräckligt länge. Vi har en tendens att övertolka dessa kluster och dess betydelser.
One of the concepts that gets the media excited and brings a glow of expectation to the eyes of compensation lawyers is the cluster. Every time there is a disease outbreak, cluster-watching comes back into vogue, as is now happening in the UK during the foot and mouth epidemic.
The extreme value fallacy förklarar lite om en viss typ av elakartad 'data snooping' som övertolkar att det alltid finns någon som har högst eller lägst värde. Artikeln ger också en kort introduktion i den fascinerande statistiska tekniken extremvärdesanalys.
A very common example is the birth month fallacy, which recurs in the media several times a year. It usually takes the form of a headline such as People born in July are more likely to get toe-nail cancer or more fancifully Cancerians are more likely to get toe-nail cancer. What the 'researchers' have done is look at the statistics for each of the twelve months, pick out the biggest, and then marvel that it seems large compared with what you would expect for a random month.
Birth daze gör en något mer matematisk genomgång av ovanstående.
It's a record!: Rekord kan, per definition, endast förbättras. Artikeln diskuterar lite om konsekvenserna av detta enkla faktum.
(Det var bland annat ovanstående artiklar som fick mig att intressera mig för just ämnet extremvärdesanalys för ett bra tag sedan.)
Sajten där dessa artiklar finns, Number Watch, är en ständig källa till intressant, ibland provokativ, läsning. Programförklaring: This site is devoted to the monitoring of the misleading numbers that rain down on us via the media. Whether they are generated by Single Issue Fanatics (SIFs), politicians, bureaucrats, quasi-scientists (junk, pseudo- or just bad), such numbers swamp the media, generating unnecessary alarm and panic. ... .
Frequently Asked Questions ger en bra översikt över saker som behandlas.
Posted by hakank at 09:17 FM Posted to Dynamiska system | Statistik/data-analys | Comments (2)
juli 31, 2003
Journal of Statistics Education
Journal of Statistics Education (JSE) är en öppen elektronisk tidskrift utgiven av American Statistical Association (ASA). Tidskriften inriktar sig främst mot dem som utbildar i statistik och sannolikhetteori på olika nivåer.
I det senaste numret finns några småtrevliga artiklar:
- The Pedagogy and Probability of the Dice Game HOG
- "It’s like... you know": The Use of Analogies and Heuristics in Teaching Introductory Statistical Methods
För den som själv vill leka finns datafilerna till artiklarna att ladda ner här.
Anledningen till att jag tycker om att läsa den här typen av tidskrifter (dvs riktade mot utbildare) är att de ofta har intressanta vinklingar på ämnet och pedagogiska exempel, vilket ju alltid underlättar när man håller på att lära sig något nytt eller vill förkovra sig i ämnet. Eller helt enkelt om man vill förstå grunderna bättre. Jag tror det är nyttigt att då och då gå tillbaka till grunderna, eftersom man (in-)ser nästan alltid något man missade förra gången man lärde sig det.
Posted by hakank at 01:17 EM Posted to Statistik/data-analys
juli 23, 2003
Chance News (och sajt)
Senaste numret av Chance News (May 2, 2003 .. July 20, 2003) är nu ute.
För den som inte kommit i kontakt med denna skrift kommer en liten kort beskrivning. Chance News samlar och kommenterar nyheter, notiser etc om användande (ofta missbrukande) av sannolikhetsteori och statistik, främst i olika populärmedia. Ofta avslutas en sådan notis med en liten övning åt läsaren. Målgrupp för tidningen är nog främst lärare i matematik, statistik och sannolikhetsteori och forskare som använder dessa verktyg samt journalister, men även den allmänna massan (som jag alltså tillhör) kan få ut mycket av denna tidning.
Notiserna kan vara mycket korta eller långa analyser. Alla nummer sedan 1992 finns arkiverade. Längst ned på första sidan kan man söka bland notiserna. T.ex. en sökning på Robert Matthews.
Det föreliggande numret tar bl.a. upp en rapport om att företag som tagit bort internetkopplade attribut från sitt namn (.com, .net etc) förbättrar sina resultat, några Marilyn vos Savant-svar, en redogörelse för sannolikheterna i ett val i Texas (USA), resultat från forskning om passiv rökning, likheter mellan olika språk (lite om Zipfs lag), etc.
På samma sajt finns det även några utomordentliga (RealAudio) föreläsningar hållna på en "populärnivå". Några i högen (finns lite längre ned på sidan):
- Susan Holmes: "Probability by Surprise: Teaching with Paradoxes and Animations". Pratar om och visar hur simuleringar används i sannolikhetsteoriundervisningen.
- Tom Gilovich: "Streaks in Sports", beskriver om det verkligen finns "streaks" (följder av tur) i sporter (en ubikuös myt hos många). Gilovich har f.ö. skrivit den alldeles förträffliga boken How We Know What Isn'T So, som beskriver varför/hur vi tänker irrationellt ibland (eller ofta).
- Ray Hyman: "Statistical Issues in ESP Research" redogör för olika försök inom ESP. Ray Hyman är en av de mest kända skeptikerna inom området.
- samt några kritiska röster om Bibelkoden
Läs gärna även lite artiklar/böcker på Articles and Books.
Posted by hakank at 09:56 EM Posted to Statistik/data-analys
juli 11, 2003
Resampling - Statistik utan tårar
När jag nu läser om systemdynamik och dess förespråkare har jag flera gånger kommit att tänka på Julian Simons Resampling-projekt som innebär att lära ut 'statistisk utan tårar'.
En parentetisk not: Julian Simon är möjligen mer känd som en "miljöoptimist"/"teknikoptimist" vilket - intressant nog - går stick i stäv mot slutsatser som vissa systemdynamiker kommit fram till. Se till exempel Julian Simons Bet. Notera att jag inte alls är någon expert i denna debatt, knappast - och tyvärr - inte ens newbie. Jag vet inte heller om Simons miljöoptimism är kopplad till hans resamplingprojekt på något sätt, men inget jag läst i hans resamplingsskrifter har antytt detta, mer än möjligen i något förfluget exempel.
Efter denna utvikning: tillbaka Simons resampling. Simon var mycket kritiskt till hur statistisk analys lärs ut i skolorna och används av statistiker. Den statistika formalismen - menar Simon - har dels som konsekvens att det är få som förstår vad statistikerna pratar om och därmed har svårt att följa tankegångar och slutsatser som bygger på statistisk analys. Dels passar den statistika teorin endast för vissa typer av problem som ofta inte är speciellt realistiska i "den verkliga världen". Ett annat problem är att även enklare sannolikhetsteoretiska resonemang är svårt för en icke invigd att ta till sig. Hans lösning var att man i stället skulle lära ut en teknik för att göra analyser tillgängliga för alla - en statistik utan tårar.
Likheten mellan Simon och systemdynamikerna är att man försöker få ut ett mer tillgängligt sätt att använda matematiska metoder till dem som inte är matematiskt skolade. För Simon var det den matematiska statistiken som kritiseras, för systemdynamikerna var det dynamiska system med differens-/differentialekvationer. Båda mycket lovvärda projekt!
Här kan man också jämföra med t.ex. John Allen Paulos Innumeracy, som är en mycket arg och mycket bra bok om att vi är väldigt dåliga på att förstå även enkla statistiska/sannolikhetsteoretiska resonemang och konsekvenserna av detta. Paolos böcker ger dock ingen systematisk lösning på hur man löser problemet, villket Simon gör.
Simons lösning heter alltså resampling, vilket helt enkelt innebär är att man simulerar problem i stället för att försöka få in dem i statistikens matematiska apparat (som kan vara mycket komplicerad att förstå). Simuleringen görs genom att programmera problemet med ett programspråk. Simon skapade ett system med ett eget programspråk, Resampling Stat, som endast är till för sådana simuleringar, vilket gör det enkelt att förstå och använda. I ärlighetens namn måste jag säga att jag inte kört just Resamplig Stats speciellt mycket; i stället har jag använt statistikspråket R, Java eller andra generella språk. Däremot har jag översatt mycket Resampling Stat-kod, och kortare tester med Resampling Stats gör att jag tycker det verkar lätt att använda för någon som inte har programmeringserfarenheter.
Väldigt mycket mer om Resamplig Stats finns på www.resample.com. En utomordentligt trevlig introduktionsbok Resampling: The New Statistics finns online.
Båda systemdynamikernas och Simons resamplingsmetoder går alltså ut på att förstå verkliheten genom att simulera den, däremot gör systemdynamikerna det vanligen i mycket mer grafiskt aptitliga system.
För några månader sedan skrev jag en hel del om resampling etc i Lite om resampling, simulering, sannolikhetsproblem etc. som jag hänvisar till. Sidan innehåller en hel del relaterade länkar, och en massa simuleringar (skrivet främst i R) av sannolikhetsteoretiska problem av olika digniteter.
Personligen anser jag att man bör, om det är möjligt, kombinera (Simons) simuleringsmetoder och mer formell statistisk analys. Man kan t.ex. använda resampling/simulering för få en känsla för problemet, prototypa problemet, kontrollera resultat eller om man inte är expert inom statistisk analys.
I den (formella) statistiska analysen finns det även något som heter resampling som har mycket av Simons idé, och är en accepterad och matematiskt väl underbyggd teori. Men den är inte lika enkel att ta till sig som Simons mer pedagogiska variant.
Ett tips är att börja läsa Simons skrifter och sedan läsa mer formell statistik och sannolikhetslära. En utmärkt introduktion i sannolikhetslära är Introduction to Probability av Charles M. Grinstead och J. Laurie Snell, som också använder mycket simulering för att visa hur begreppen hänger i hop. Det finns kod skriven i Mathematica, Maple, True Basic och Java Applets. Själv gjorde jag exempel och övningar i R.
En utmärkt svensk bok om sannolikhetsproblem är Sant eller sannolikt : Tankar kring matematik, statistik och sannolikheter av Allan Gut. Det är dock ingen lärobok utan innehåller en mängd essäer i ämnet.
En sista not: Jag har även testat att modellera några enklare sannolikhetsproblem, av den typ som Simon koncenterar sig på, i systemdynamikprogrammet Vensim. I vissa fall kändes de inte riktigt lika enkelt som att programmera problemen i R eller Java, möjligen är detta en vanesak. Fortsatt forskning pågår...
Posted by hakank at 11:15 FM Posted to Dynamiska system | Statistik/data-analys
juni 25, 2003
Kedjebrevsanalys
Efter att ha funderat lite på utvecklingen och förändringar av blogg-berättelser kom jag i morse att tänka på en rolig liten sak jag läst för ett antal år sedan, Linking Chain Letters (Postscript) av Charles Bennett, Ming Li och Bin Ma. Här analyserar man olika varianter av samma kedjebrev (i faxform) för att undersöka hur de utvecklats, vilka som är varianter av andra etc. Se även projektets webbsida som innehåller de kedjebrev som används i analysen.
Detta är i princip samma problem som när man ska bestämma släktskap hos arter inom biologin med s.k. fylogenetisk analysis, där man utrönar likheterna mellan arterna för att skapa ett utvecklingsträd. Här är en Java-grunka som visar detta.
När jag var ute på staden i eftermiddags upptäckte jag, märkligt nog, att Juni-numret av Scientific American har en populariserad version av ovanstående paper. (Den refererade sidan visar endast ett litet utdrag.)
Ovanstående författare är värda att kolla in mer, speciellt Charles Bennett som har skrivit bland annat om kvant-teleportering och informationsteori.
Posted by hakank at 09:36 EM Posted to Statistik/data-analys
juni 23, 2003
Bayesian Networks
I morse läste jag med spänning Thorvald Freiholtz översikt av system dynamics (Torsksystemdynamik) och de referenser han hänvisade till.
En sak jag kom att tänka på under läsningen var Bayesianska nätverk (BN).
BN är en typ av "grafisk modellering" som bygger på sannolikhetsteoretiska relationer (Bayes regel) mellan olika typer av variabler (entiteter, fenomen) vilka är sammankopplade i en graf.
Genom att laborera med olika förutsättningar i en sådan modell kan man få reda på hur detta påverkar resten av systemet. T.ex. kan man modellera kopplingar mellan symptom och sjukdom (t.ex. som ett expertsystem), sannolikhetsteoretiska problem (t.ex. Monty Hall-problemet). En viktig del i modelleringen är att man kan gå från orsak till verkan, och även studera orsaken givet verkan, t.ex. om en patient är sjuk (verkan), kan man se vilka möjliga orsaker det finns. Ytterligare en intressant sak med BN är att man utifrån existerande data kan automatiskt skapa en modell.
Personligen har jag använt BN mest för att modellera mer eller mindre rena sannolikhetsteoretiska problem.
Några introduktioner till ämnet:
- Charniaks Bayesian Networks without Tears (PDF)
- Kevin Murphy A Brief Introduction to Graphical Models and Bayesian Networks. Har många vidarelänkar.
En utmärkt introduktion i sannolikhetsteori, där bland annat Bayesiansk analys ingår, är
Introduction to Probability av Grinstead och Snell.
Av en lite märklig slump kom senare under dagen ett mail från Hugin, en av de främsta produktutvecklarna av sådana system, om att det kommit en ny version av systemet. När jag kollade in Bayesianska nätverk använde jag bland annat deras demoversion som var alldeles utmärkt för enklare modellering.
Hugin har bra introduktionsdokumentation hur man arbetar i systemet, t.ex. Getting Started, Tutorial och kommer med en massa exempel varav några är väl dokumenterade, t.ex. modell av Monty Hallproblemet.
Det finns en begränsad demo av Hugin att ladda ner här. Finns för Windows, Linux samt Solaris. Tyvärr är Hugins demo-version alldeles för begränsad för att man ska ha någon riktig nytta av dess möjligheter att automatiskt skapa en BN-modell.
Det finns naturligtvis även andra BN-produkter, se t.ex. googles Computers/Artificial_Intelligence/Belief_Networks/-katalog.
Posted by hakank at 08:55 EM Posted to Machine learning/data mining | Statistik/data-analys