« Monte Carlo Simulation in Excel: A Practical Guide | Main | LinkRanks »
december 12, 2004
Fraktalbloggare?
I Artikeln om bloggning i InternetWorld myntar Annica Tiger begreppet "Nollbloggar" (och hon utvecklar detta lite i Nollbloggar). Betydelsen är att i många bloggar kommenteras det aldrig eller mycket sällan i. Den förstnämnda artikeln är skriven - bör noteras - med glimten i ögat, men med en viss ironi (och detta motto torde väl stå för den innevarande blogganteckningen också).
Annica Tigers blogg tillhör ju den andra gruppen bloggar, dvs den där det alltid är fullt med långa diskussioner och dit man gärna går och läser. Men vad ska man kalla sådana bloggar som Annicas, dvs motsatsen till noll-bloggar? Kanske "Ett-bloggar"?
Kommen så långt i tankarna kom begreppet "fraktal-bloggar" upp. Det skulle motsvarar de bloggar som ligger mitt emellan de båda extremerna: har ibland många kommentarer men oftast är det inga eller ett fåtal.
Steget till att undersöka hur det ligger till med detta för en näraliggande blogg var naturligtvis inte långt. Så här är fördelningen av antal kommentarer på hakank.blogg och hur många blogganteckningar som har detta antal kommentarer.
Antal kommentarer: Antal anteckningar
0: 498
2: 66
1: 50
4: 35
3: 34
5: 19
6: 10
8: 10
7: 7
9: 4
10: 3
11: 2
14: 2
21: 1
12: 1
23: 1
Förklaring: Det finns 498 blogganteckningar som har 0 kommentarer, 66 anteckningar med 2 kommentarer osv. Samt en långkörare med 23 kommentarer; glädjande nog en som eventuellt fortfarande pågår: Skånsk bloggaremiddag: en sammanfattning.
(Man kan här notera att det finns fler anteckningar med 2 kommentarer än med 1 kommentar, och fler med 4 kommentarer än med 3 Detta beror på att jag försöker att svara på alla kommentarer så en gästkommentarer resulterar i en egen kommentar, in alles 2. Att det är så pass många som 50 anteckningar med endast en kommentar är lite skamligt.)
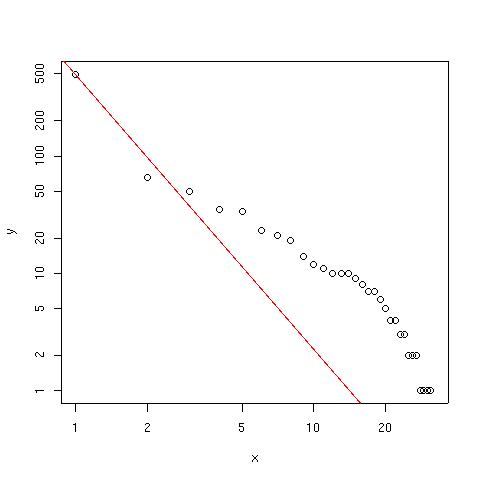
Här är en bild som åskådliggör detta. Den röda linjen är ett försök att göra en linjär regression över datan.
Som förklarades mer i den liknande analysen Statistikknarkande: Antal webb-besökare och power law kan man räkna ut en koefficient för denna regressionslinje, vilket för den nu studerade datan är 2.33.
Alltså: Jag är en (fraktal) 2.33-bloggare!
För mer information om power laws och fraktaler hänvisas till den ovan nämnda Statistikknarkande: Antal webb-besökare och power law.
Man bör dock komma ihåg nedanstående citat från Mandelbrot (citerades bl.a. i Benoit Mandelbrot intervjuad i New Scientist: A fractal life) som tar udden ur en del av fraktal/power law-forskningen: [Question:] Fractals seem to appear all over nature and in economics. Even the internet is fractal. What does that say about the underlying nature of these phenomena?
[Mandelbrot:] Well, it depends on the field. Circles and straight lines also appear everywhere. Does this mean that all those phenomena have something in common? Of course not. The roughly circular trajectory of a planet around the sun is due to gravitational interactions. Berries are round because a sphere has a smaller skin. The beauty of geometry is that it is a language of extraordinary subtlety that serves many purposes.
Lustigt nog fick hakank.blogg (bland andra) ett annat värde idag, nämligen 0.36. Det var i Lemonad-jonas o/ordning-anteckning cirkelresonemang 2. Värdet gäller förhållandet mellan antal länkar i blogganteckningarna och antal länkar till sin egent blogg. (Jag funderar fortfarande vad detta värde egentligen innebär och återkommer till Jonas om något kommes på.)
Så på samma dag helg har vi fått två matematiska dimensioner för bloggar:
* antal självrefererande länkar
* fördelningen av kommentarer
Ska vi försöka hitta en tredje så att det blir en fin tredimensionell modell?
Posted by hakank at december 12, 2004 12:11 FM Posted to Blogging | Statistik/data-analys
Comments
Det där är ju toppen! Vi borde nog försöka värva dig till o/ordning :) Kommer du på någon data du skulle vilja ha från bloggkartan är det bara att säga till! Återigen, riktigt bra :)
Posted by: jonas (lemonad) at december 12, 2004 03:56 FM
Skoj du tyckte om det, Jonas.
Jag har faktiskt funderat på att be dig om data just för att kunna göra lite roliga analyser, kanske något mer kring dina self-refs.
Men vi kan väl ta den diskussionen lite mer utanför bloggen? (Eller kanske vi ska ta den här så blir det fler kommentarer. :-)
Posted by: hakank ![[TypeKey Profile Page]](http://www.hakank.org/webblogg/nav-commenters.gif) at december 12, 2004 07:20 FM
at december 12, 2004 07:20 FM
(fast hur kommenterar man på din blogg? får "denied due to questionable content" så snart jag skriver mer än en rad)
Posted by: Fredrik at december 12, 2004 03:18 EM
Fredrik: Troligen är det något speciellt ord som systemet inte tycker om, elle kanske en URL som matchar någon av no-no-regexarna.
Du får gärna maila mig på hakank@bonetmail.com så kan jag lägga upp kommentaren.
För nu har jag ju blivit väldigt nyfiken på vad du skrev.
Posted by: Håkan Kjellerstrand at december 12, 2004 05:12 EM
Jag mejlade dig men tänkte att det är bäst jag svarar här ifall andra är intresserade (plus att jag ju vill förbättra din framtida statistik :)
Tanken är att all data från bloggkartan skall finnas tillgänglig för alla men just nu finns bara delar tillgängliga via xml/dtd-länkarnai bloggkartans vänsterkolumn. Om någon har något specifikt den skulle vilja få tillgång till så kan det säkert ordnas ändå.
Posted by: jonas (lemonad) at december 12, 2004 06:12 EM
Som jag kommer att maila dig (ev. i kväll) så är jag naturligtvis intresserad av hela din datarymd. Det spelar för egen del ingen roll om det är i XML-format, vanlig ASCII eller en databasdump med INSERT-satser etc, eftersom datan måste troligen ändå preprocessas vidare "manuellt" på något sätt.
Posted by: hakank ![[TypeKey Profile Page]](http://www.hakank.org/webblogg/nav-commenters.gif) at december 12, 2004 06:28 EM
at december 12, 2004 06:28 EM
[Följande kommentar skrevs av Fredrik på http://effbot.org/ , men lades in av mig (hakank) eftersom det inte funkade när Fredrik gjorde det. Och jag har inte hittat den sträng som stoppar kommentaren.]
"Men vad ska man kalla sådana bloggar"
Fikabordsbloggar, eftersom dom företrädesvis tar upp allmänna ämnen ("jag läste i tidningen att..." "är det inte hemskt med alla dessa...") som alla kan ha åsikter om. Dialogen är viktigare än analysen.
Specialistbloggar (som din och, stundtals, min) är något helt annat. Där antar läsaren att specialisten faktiskt vet vad han pratar om, och nöjer sig oftast med detta.
(jfr. Parkinsons "Bike Shed Effect")
Posted by: hakank ![[TypeKey Profile Page]](http://www.hakank.org/webblogg/nav-commenters.gif) at december 12, 2004 07:30 EM
at december 12, 2004 07:30 EM
Fredrik: Du har en stor poäng.
Jag tror dock inte att det räcker med att en blogg tar upp vilka fikabordsämnen som helst för att göra den till "ettbloggare". Det krävs nog något mer för att få andra att diskutera livligt, t.ex. att ämnena ska vara tillräckligt intressanta att diskutera (och intressant skrivna), och att de man diskuterar med stimulerar till vidare diskussioner.
Sedan sätter väl den vanliga principen igång att man försöker komma in på ställen där det redan är mycket folk, dvs Matteus-principen: "åt den som har ska vara givet" (och som sägs vara en betydande orsak till det sociala power law-beteendet).
Tack för Parkinson-kopplingen, förresten. För framtida referenser lämnas en länk till en förklaring:
http://linuxmafia.com/~rick/lexicon.html#bikeshed .
Posted by: hakank ![[TypeKey Profile Page]](http://www.hakank.org/webblogg/nav-commenters.gif) at december 12, 2004 08:59 EM
at december 12, 2004 08:59 EM
Tredje? Vad säga om antal trackbacks? :)
Posted by: Dabitch/Åsk at december 13, 2004 09:18 EM
Åsk: Intressant, men är det inte lite för ... okomplicerat.
Kanske:
(2 * totalt antal trackbacks - 3 * självtrackbacks + antal kommentarer man inte själv skrivit på din blogg) / (antalet blogganteckningar)
Hmm, fick inte in Pi eller E denna gång. Rackarns också...
:-) <--- OBS!
Posted by: hakank ![[TypeKey Profile Page]](http://www.hakank.org/webblogg/nav-commenters.gif) at december 13, 2004 10:23 EM
at december 13, 2004 10:23 EM
Kul att hitta lite matematik :-)). Kul resonemang, gillar sån't! Jag måste protestera mot den linjära regressionen dock, du får nog räkna en gång till ... det ser inte precis ut som linjen är en anpassning till de data som presenteras i alla fall ;-) ... (OK, OK ... jag erkänner, jag slängde iväg en beräkning också.)
Men fraktal ... ja, det betyder något som är sönderbrutet, "oregelbundet", tja, kanske man kan kalla det. Då bör du med en liten ansträngning kunna åstadkomma hakanmängden ur dina data. Plotta den sedan som en tvådimensionell bild (du kan ju använda sammanlagda antalet ord i kommentarerna också som extra variabel för att få färg i bilden) så kanske det börjar likna något :-))! Jag ser fram emot att få se den bilden!
Posted by: Thebe at december 15, 2004 09:47 EM
Thebe: Visst är det skoj med matematik. Du har självklart rätt i att regressionslinjen inte är perfekt. Tänk bara på att båda axlarna är i log-log.
Bilden är alltså gjord med samma teknik som den bild som visas på "Statistikknarkande: Antal webb-besökare och power law", http://www.hakank.org/webblogg/archives/000204.html (som refereras till i texten ovan och också innehåller referenser till många bra skrifter i ämnet).
Sådana log-log-bilder är det vedertagna sättet att visa att det är någon form av power law-fördelning med i spelet, och det var därför denna bild skapades på detta sätt, med alla dess fel och brister (se nedan för några).
Som sagt bilden är långt ifrån perfekt, men jag tror inte det gör så mycket eftersom det var principen jag var ute efter: en "fraktalblogg" är en blogg med många anteckningar som har få eller inga kommentarer och få anteckningar med många kommentarer.
Angående "fraktal" som sönderbruten. Jag kanske missförstår din poäng här, men det är inte själva sönderbrutenheten som kännetecknar en fraktal utan själv-likheten, dvs att ett objekt ser "likadant ut" (vad man nu än menar med det) på alla eller flera nivåer. Som det står på den svenska Wikipedia:
"""
En fraktal, (ibland monsterkurva), brukar defineras som "Ett självsimulerande mönster med struktur i alla skalor", vilket betyder att det liknar sig självt på samma sätt som ett träds grenar i sin tur har likadana fast mindre grenar, en så kallad naturlig fraktal.
"""
Se vidare http://sv.wikipedia.org/wiki/Fraktal .
Det som är "sönderbrutet" är snarare dimensionen på objektet, som inte är de traditionella heltalsdimensionerna, (1, 2, 3 osv) utan något mellan dessa tal, t.ex. 2.92 som är nästan tredimensionellt men inte riktigt.
En power law-fördelning har en sådan egenskap: om man "zoomar in" i ett avsnitt ser det likadant ut som hela kurvan.
Det finns dock flera (till och med många) svagheter i min analys, speciellt i användandee av fraktalbegreppet. Här är några.
* bilden visar ingen riktig power law-fördelning, som kan bero på att det är för lite data, eller helt enkelt att antal kommentarer på en blogg inte är en "process" som skapar denna typ av fördelning
* även om det vore en power-law-fördelning är det inte säkert att det är en fraktal (i den mer strängt matematiska betydelsen)
* fraktal i den mer lösa betydelsen som jag använder det, var snarare som ett kompletterande begrepp till Annica Tigers "noll-bloggare" (inga kommentarer på bloggen) och dess motsats (dvs en blogg som alltid har mycket kommentarer). Om vi antar att den förra har "dimensionen" 0 (inga kommentarer alls) och den senare - säg - 10 (alltid jättemycket kommentarer) så är fraktalbloggare sådana som har "dimensioner" emellan dessa värden, heltal eller reella tal, i _analogi_ (det bör betonas) till det vanliga fraktalbegreppet.
* jag valde "fraktal"-bloggare eftersom det låter mycket klatchigare än "power law"-bloggare. Det senare begreppet har f.ö. i princip mutats in med en annan betydelse i bloggningssammanhang, nämligen fördelningen av antal besökare på en blogg: det finns väldigt många bloggare som har få besök, och det ett litet fåtal som har väldigt många besök, sedan finns det en strid ström av de som ligger mitt emellan (se vidare referenserna i den tidigare anteckningen).
Avslutningsvis: texten borde nog ha lite mer brasklappar och förtydliganden. Men bättre sent än aldrig...
F.ö. kan jag rekommendera den trevliga boken "Fractals, Chaos, Power Laws: Minutes from an Infinite Paradise" av Manfred Schroeder som går igenom mycket av detta. Se vidare http://www.amazon.com/exec/obidos/tg/detail/-/0716723573/002-3613635-5935253?v=glance
Posted by: hakank ![[TypeKey Profile Page]](http://www.hakank.org/webblogg/nav-commenters.gif) at december 15, 2004 11:38 EM
at december 15, 2004 11:38 EM
Klart jag fattar poängen, jag funderar i detaljer bara för att det är kul att göra det. Linjär regression brukar definieras som y = alfa+beta(x-xm), där xm är medelvärdet av x och alfa och beta regressionskonstanterna. Det var i den meningen jag inte tyckte linjen var en _linjär_ _regression_, men den "omanipulerade" datamängden. Att förmoda att det ska vara linjärt är väl iofs lika taget ur luften som att fördelningen ska vara power law. Det spelar ju mindre roll, för det är ju kul att testa bara. Undrar vad man ska anta, normalfördelning är väl första approximationen, har du testat det (bara för kul). Sen genererar ju kommentarer fler kommentarer, alltså en form av olinjäritet också. Rätt kul, man kunde tänka ett tag.
"Sönderbruten", med det menar jag till skillnad från mer _synbart_ regelbundna geometrier som en cirkel, kvadrat t ex. Men i det sönderbrutna finns förvisso ett mönster, och det var där jag tänkte du skulle skapa "hakan"-mängden, som analogi till t ex Mandelbrot- eller Julia-mängder :-)! Och man kan väl säga att blogg-kommentarer är till synes "sönderbrutna" mängder, i motsats till regelbundna, alltså.
Och jag gillar fö uttrycket "fraktal-bloggare", det är lite matematiskt tyngd i det *s*.
Posted by: Thebe at december 16, 2004 10:09 FM
OK, nu förstår jag din poäng bättre, Thebe.
Kul idé med hakank-mängden, ett möjligt framtida projekt. Tack för förslaget.
Posted by: hakank ![[TypeKey Profile Page]](http://www.hakank.org/webblogg/nav-commenters.gif) at december 17, 2004 09:49 EM
at december 17, 2004 09:49 EM