« Choco: Constraint Programming i Java | Main | Divisorträd: unika sätt att göra konsekutiva uppdelningar »
april 19, 2006
de Bruijn-sekvenser av godtycklig längd
För några år sedan skrevs ett program för att skapa de Bruijn-sekvenser, som kortfattat kan förklaras som en sträng (cykel) som innehåller ("testar") alla förekomster av delsträngar, där delsträngarna är representationer av tal. Mer förklaringar och exempel ges i de Bruijn-sekvenser (portkodsproblemet) och programmet de Bruijn sequence. I slutet finns även några andra referenser.
De metod som dessa sekvenser konstrueras ger endast stränglängder med jämna potenser, dvs 2^2 = 3, 2^3 = 8, 3^2 = 9, 3^3 = 27 osv. En fråga som ställdes tidigt var: Kan man skapa sådana sekvenser för en godtycklig längd, t.ex. 11, 17 eller 52 och för godtycklig bas, 2, 6,11 etc? Basen är alltså den kodning av talen man använder, där.basen 2 ger en binär representation (0,1), basen 3 använder 0, 1,2 osv.
Svaret på frågan är: Visst kan man det!
Än så länge har jag dock inte kommit på en vacker algoritm som den som finns för "vanliga" de Bruijn-sekvenser. Se The (Combinatorial) Object Server, Information on necklaces, unlabelled necklaces, Lyndon words, De Bruijn sequences (i slutet på sidan finns det länkar för att ladda ner källkod).
Programmet "de Bruijn arbitrary sequences"
Programmet de Bruijn arbitrary sequences visar några av resultaten av denna undersökning. Troligen behövs lite förklaringar av programmets metoder och parametrar och sådant bistår jag så gärna med.
Metoden: slumpa cykler
Principen för att skapa dessa sekvenser är enkel: Skapa en de Bruijn-graf och slumpa fram cykler i denna graf tills en av korrekt längd hittas.
Denna slumpmässighet är det som gör att programmet inte tillåts arbeta med speciellt stora värden.
de Bruijn graf
En de Bruijn-graf är en graf där kopplingarna mellan talen (noderna) följer "de Bruijn-regeln" att ett tals suffix ska vara ett annat tals prefix i deras *-ära representation. T.ex. det binära talet 000 kan kopplas till 001, talet 001 med 010 och 011 osv. Baser större än 2 hanteras på motsvarande sätt.
Exempel: Här visas kopplingarna i grafen för n = 16 i basen 2. Inom parentes visas den binära representation av talet.
0: 0 1 (0000)
1: 2 3 (0001)
2: 4 5 (0010)
3: 6 7 (0011)
4: 8 9 (0100)
5: 10 11 (0101)
6: 12 13 (0110)
7: 14 15 (0111)
8: 0 1 (1000)
9: 2 3 (1001)
10: 4 5 (1010)
11: 6 7 (1011)
12: 8 9 (1100)
13: 10 11 (1101)
14: 12 13 (1110)
15: 14 15 (1111)
Här är en mer grafisk representation (skapat med programmet dot).
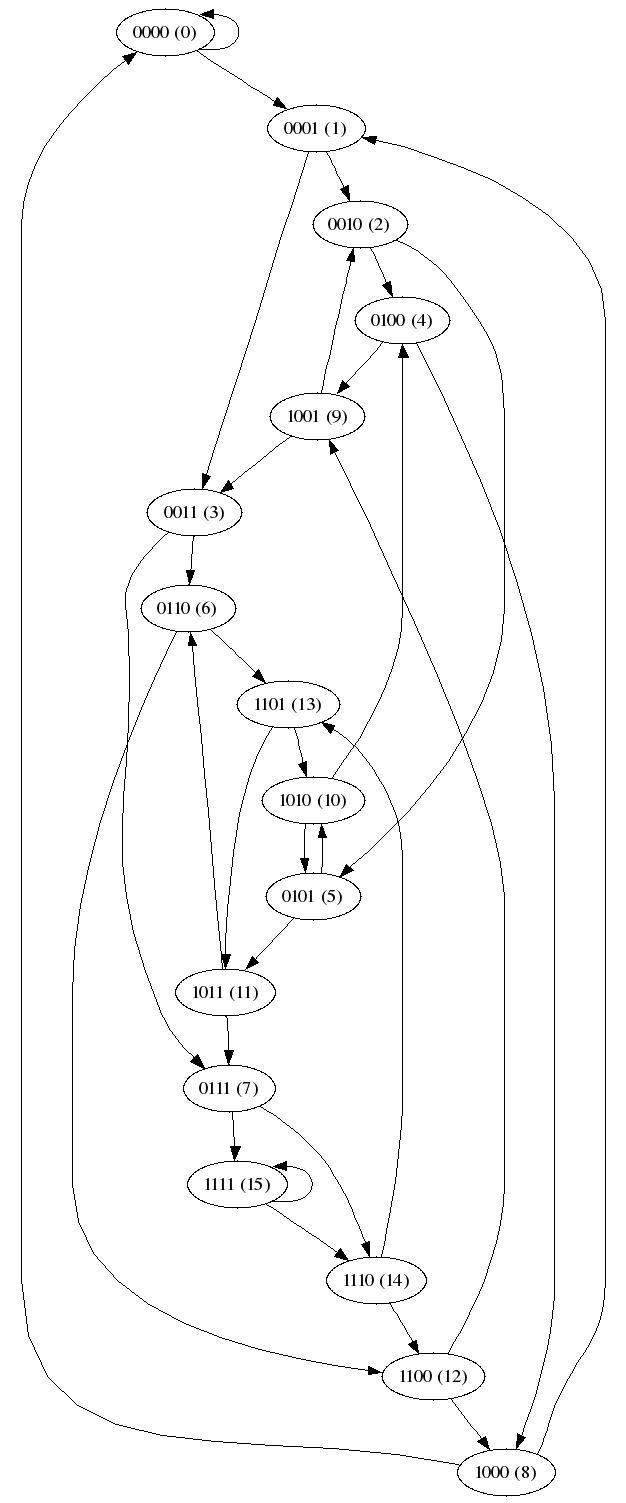 (klicka på bilden för att förstora den).
(klicka på bilden för att förstora den).
Antalet noder
Antalet noder i de Bruijn-grafen räknas ut enligt följande (motsvarar nearest_power i pseudo-koden nedan):
- om n är en jämn potens för basen används n noder (talen 0..n-1). T.ex. n=16 bas 2 är 2^3 är en sådan jämn potens.
- annars är antalet noder den närmaste efterföljande jämna potensen för basen. Exempel: För n=7 (bas 2) blir det 8 noder (2^3=8 ). För n=21 bas 3 blir det 27 noder (3^3=27 ) osv.
Kopplingsgrafen är enkel att räkna ut och principen ses nog vid närmare granskning av några exempel. Hur som helst kommer här pseudo-kod:
# nearest power in the choosen base, or N itself if N is a power
next_pow = nearest_power(N, base)
half_pow = next_pow / base;
for num (0..next_pow-1) {
for b (0..base-1) {
x = base * (num % half_pow);
conn = x + b;
graph->add_edge(num, conn); # connect num -> conn
}
}
Kort förklaring av programmet
Programmet har en del parametrar vilka här förklaras.
N (2..64): Det är stränglängden (eller antal objekt). Kan vara mellan 2 och 64.
Base (2..4): Basen som ska användas. T.ex. för bas 2 är det binär representation (0,1). Giltiga värden är 2,3 eller 4.
Type: normal / reversed: Normal innebär att sekvensen visas normalt från vänster till höger och de binära (bas-ära) talen kodas normal (7 binärt är "0111"). Det lägsta talet börjar decimalcykeln. Reversed är då man vänster på allting: de binära (etc) koderna är omvända (7 visas som "1110") och det högsta talet i decimalcykeln visas först.
Show connections: Visar kopplingarna för den de Bruijn-graf som byggs upp.
Show sequence: Här visas de individuella representationerna.
Exempel
Här är ett exempel på på en av många möljiga sekvenser för n = 52 i basen 4:
Sequence:0001012131301132230220330300323123212013332002102331
Cycle (in decimal): 0 1 4 17 6 25 39 29 55 28 49 5 23 30 58 43 44 50 10 40 35 15 60 51 12 48 3 14 59 45 54 27 46 57 38 24 33 7 31 63 62 56 32 2 9 36 18 11 47 61 52 16
Sequence check:
000101213130113223022033030032312321201333200210233100
000 (0)
001 (1)
010 (4)
101 (17)
012 (6)
....
Begränsningar
Som ovan nämnts bygger programmet på en slumpning av cyklerna. Det kan ta en stund att slumpa fram cykler av korrekt längd i stora grafer så finns det några begränsningar för att datorn inte ska bli sönderkörd:
N: mellan 2 och 64
base: mellan 2 och 4
Om någon läsare nu (eller sedan) upplever ett starkt behov av sådana sekvenser med större längd / bas så är det bara att kontakta mig (hakank@bonetmail.com så kan vi säkert ordna något.
Vidare utveckling
Denna slumpmässiga metod fungerar om det är relativt små värden av N och bas. Men för större värden är det inte en tillgänglig metod. I stället bör en deterministisk algorim skapas.
Ett pågående projekt är också att försöka minska antalet noder i grafen så att det inte blir så många möjliga cykler att leta igenom.
Not
Jag är osäker på om ovanstående fortfarande kan kallas för en de Bruijn-sekvens när man använder denna alternativa approach.
Se även
de Bruijn sequence (den "vanliga" formen)
de Bruijn-sekvenser (portkodsproblemet)
MathWorld deBruijnSequence
COS: Information on necklaces, unlabelled necklaces, Lyndon words, De Bruijn sequences
Posted by hakank at april 19, 2006 06:52 EM Posted to Matematik | Program