hakank.blogg

« de Bruijn-sekvenser av godtycklig längd | Main | Blogglunch söndagen tjugotredje april tjugohundrasex/tvåtusensex/i år »

april 22, 2006

Divisorträd: unika sätt att göra konsekutiva uppdelningar

Vilka - och hur många - unika sätt kan man göra följande "konsekutiva delningar" av ett antal saker. Tänk t.ex. på de olika unika sätt man kan dela upp N antal spelkort i olika högar. Metoden man arbetar med är följande:

- börja med en hög av N saker

- dela upp dessa saker i ett antal högar så att det är lika många saker i varje hög

- ta en av dessa högar och fortsätt på samma sätt tills det bara finns
en sak i varje hög

Eller på ett något mer matematiskt språk: på vilka - och hur många - olika unika sätt man kan dela upp ett tal i dess divisorer (förutom 1 och talet själv).

Not: Eftersom nedanstående inte har (matematiskt) bevisats så är det endast en hypotes (en förmodan).

Uppdatering. Hmm, jag har hittat en inkonsekvens i nedanstående. Inte bra. Återkommer...

Program: Divisor tree
Det program som används för att undersöka dessa konsekutiva delningar är Divisor tree / / Consecutive dealing in heaps. Nedanstående förklaringar är förhoppningsvis tillräckligt för att förklara programmet.

Notera att programmet endast arbetar med värden mellan 2 och (lite halv godtyckligt) 30000 av datorsnällhetsskäl.

Inledande exempel
Låt oss göra det mer åskådligt med 16 saker (t.ex. 16 spelkort).

För N = 16 finns det 4 olika sätt.


16 / 2 heaps = 8 things in each heap (2 -> 8 -> ..)
     8 / 2 heaps = 4 things in each heap (2 -> 4 -> ..)
         4 / 2 heaps = 2 things in each heap (2 -> 2 -> 1)
     8 / 4 heaps = 2 things in each heap (4 -> 2 -> 1)
16 / 4 heaps = 4 things in each heap (4 -> 4 -> ..)
     4 / 2 heaps = 2 things in each heap (2 -> 2 -> 1)
16 / 8 heaps = 2 things in each heap (8 -> 2 -> 1)

Found 4 ways for N = 16.


Beskrivning av det första (unika sättet):
* Först har vi 16 saker.
* Dessa delas upp i två högar med 8 saker i varje hög.
* Vi tar en av dessa två högar och har nu en hög med 8 saker. Denna delar vi upp i 2 högar så vi får 4 saker i varje hög.
* Vi tar en av dessa högar och delar upp i 2 högar med två saker i varje hög.
* Vi tar sedan en av dessa högar och delar ut i 2 högar med 1 sak i varje hög.

Men sedan kan vi inte gå vidare eftersom det nu är endast 1 sak i varje hög. Man skulle i och för sig kunna dela upp 1 sak i 1 hög i det oändliga men det är inte tillåtet i detta spel. Regel: När det endast finns 1 sak i en (färdigutdelad) hög är man klar med denna uppdelnin.

Antal saker som fanns i de högar vi använder under utdelningen är: 16, 8, 4, 2, (1).

Tittar vi på exempelkörningen ser vi att en unik väg (ett unikt sätt) är avslutat om raden avslutas med -> 1. Står det däremot -> .. så fortsätter uppdelningen och man går vidare till nästa (inskjutna) rad. Denna trädliknande struktur är anledningen till att det kallas för divisorsträd där de olika uppdelningssätten grenar ut sig. (Möjligen skulle det kunna kallas för divisorsstad eftersom det är vägar vi pratar om eller divisorsskog efterom det är flera träd med olika grenar, men ingendera av dessa känns lika naturligt som -träd).
De 4 olika sätten för N = 16 är följande, där talen anger antal saker i varje hög. Den första raden motsvarar alltså den långa beskrivningen ovan.

16 -> 8 -> 4 -> 2
16 -> 4 -> 2
16 -> 4 -> 2
16 -> 8 -> 2


För N=12 finns det 5 vägar (avslutas med 2 eller 3)

12 / 2 heaps = 6 things in each heap (2 -> 6 -> ..)
     6 / 2 heaps = 3 things in each heap (2 -> 3 -> 1)
     6 / 3 heaps = 2 things in each heap (3 -> 2 -> 1)
12 / 3 heaps = 4 things in each heap (3 -> 4 -> ..)
     4 / 2 heaps = 2 things in each heap (2 -> 2 -> 1)
12 / 4 heaps = 3 things in each heap (4 -> 3 -> 1)
12 / 6 heaps = 2 things in each heap (6 -> 2 -> 1)

Found 5 different way(s) for n = 12.


Primtal
Om det finns ett primtal antal saker i en hög finns det endast ett sätt (en väg) att dela upp i lika antal högar, nämligen att dela så att det finns en sak i varje hög. T.ex. om man har 13 kort så kan man endast dela ut dem i 13 olika högar med 1 kort i varje hög.

En väg avslutas alltså om det blir en hög innehåller primtal stycken saker. Eller mer korrekt: Om det är primtal antal stycken blir nästa uppdelning så många högar med 1 sak i varje hög.

Primtalskvadrater
För 4 saker så finns det bara ett sätt: nämligen att dela upp i två högar med två saker i vardera.

4 / 2 heaps = 2 things in each heap (2 -> 2 -> 1)

Found 1 different way(s) for n = 4.


Detta är ingen slump. För varje kvadrat av primtal (2^2=4, 3^2=9, 5^2=25, 7^2=49 osv) så finns det endast ett sätta att göra uppdelningen.

Båda dessa specialfall, primtal och primtalskvadrater utnyttjas i den rekursiva algoritm för att räkna ut antalet unika konsekutiva uppdelningar, och som beskrivs nedan.

Antal uppdelningar, heltalssekvenser
Om man nu räknar antalet unika sätt att göra denna typ av uppdelningar för N = 1.. 32 får vi följande heltalssekvens:


1,1,1,1,1,2,1,2,1,2,1,5,1,2,2,4,1,5,1,5,2,2,1,12,1,2,2,5,1,9,1,8


Här är en graf över sekvensen för N = 1 .. 512:

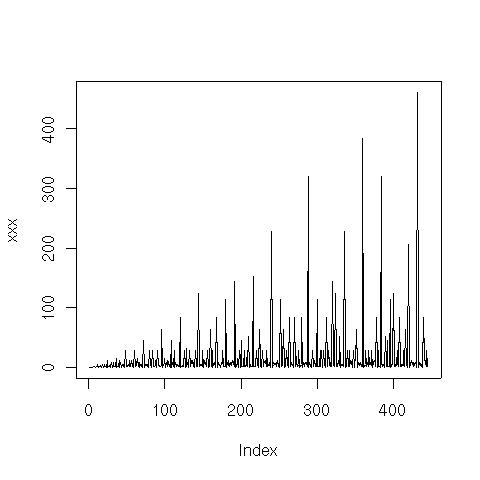
Ett bra sätt att analysera denna typ av matematiska (eller algoritmiska) strukturer är att se om det finns andra strukturer som har samma heltalssekvens. Det gör man lämpligen via On-Line Encyclopedia of Integer Sequences (som beskrivits tidigare i Heltalssekvenser). Ovanstående sekvens fanns inte med! Inte heller hittades sekvensen via superseeker som är en tjänst där man mailar in sekvensen och där systemet gör väldigt många olika typer av transformationer av sekvensen. Inte heller där hittades sekvensen.

Så det verkar som om ovanstående sekvens är ganska ovanlig. Lite märkligt eftersom det känns som en "naturlig" metod. Vi ser nedan att det är en "kusin" till en känd heltalssekvens.

Rekursiv definition
Ovanstående sekvens räknades ursprungligen ut genom att skapa vägarna i en tidig version av programmet Divisor tree, men sedan skapades (upptäcktes) en metod för att räkna ut dessa värden mycket enklare. Här är pseudokoden för metoden:


divtree(n):
   # n > 0
   if n == 1 then value = 1 # specialfall för n = 1
   elsif prime(n) then value = 1 # primtal
   else if prime_square(n) then value = 1 # kvadrat av ett primtal
   else if # annars: loop igenom divisorerna av n
     for div = divisors(n) do
     next if div == 1 or div == n # se kommentaren nedan
     value = value + divtree(div) # summera divisorernas värden rekursivt

   return value


Notera raden med "next" i for-loopen. Den innebär att om divisorn är 1 eller n så adderar man inte något värde för denna divisor. (Det är genom att förändra next-raden som vi hittar sekvensens kusin. Se nedan) Notera också att det är en rekursiv definition.

Pratversionen av metoden är ungefär: Om N är 1, ett primtal eller en primtalskvadrat så finns det ett unikt sätt att göra en delning. Om N är något annat så summerar man divtree-värdena för N:s divisorer (alla divisorer förutom 1 och N själv).

Det tarvar kanske ett exempel på detta, så låt oss titta på N = 24 (dvs 24 saker). Först divisorsträdet:

24 / 2 heaps = 12 things in each heap (2 -> 12 -> ..)
     12 / 2 heaps = 6 things in each heap (2 -> 6 -> ..)
         6 / 2 heaps = 3 things in each heap (2

Posted by hakank at april 22, 2006 11:09 FM Posted to Matematik | Program

Comments

Jag är , men ändå inte riktigt med på noterna.

Din inledande fråga är på hur många sätt man kan dela upp ett tal i sina divisorer förutom 1 och talet självt.
Då borde 1 och alla primtal returnera 0 (noll) eftersom de inte kan delas upp vidare, medan en primtalskvadrat borde returnera 1 eftersom den kan delas upp på ett enda unikt sätt.

Eller har jag missuppfattat något redan här?

Posted by: Håkan (hakke) at april 29, 2006 03:07 EM

Hakke: Det du säger är en del i konstigheten i konstigheterna i programmet/beskrivningen.

Vad gäller uppdelningar i högar man kan man dela upp t.ex. 7 saker (7 är ett primtal) på ett (1) sätt, nämligen i 7 olika högar med 1 sak i varje hög. Den metod jag använder är dock inkonsekvent (men deterministisk) och räknar uppdelningar av primtal saker ibland som 1 och ibland som 0.

Posted by: hakank at april 29, 2006 08:21 EM