« mars 2006 | Main | maj 2006 »
april 27, 2006
Smith code: Kod i Dan Browns Da Vinci-kod dom
I Expressen-artikeln Dan Brown-domaren smög in en kod i domen står att läsa:
Det är något mystiskt med domen som friade författaren Dan Brown från plagiat.
Det finns en kod i den.
Domare Peter Smiths kod....
Plötsligt dyker det upp en kursiverad bokstav mitt i ett ord. Där kan exempelvis plötsligt stå "claimant".
Lägg ihop de kursiverade bokstäverna i de första sju paragraferna och man får: Smithy code -Smithykoden.
Om man nu tar samtliga kursiverade bokstäver (de som kursiverades via programmet pdftohtml) får man följande sträng
smithycodeJaeiextostgpsacgreamqwfkadpmqzv
Den första delen - "smithycode" - nämndes i Expressen-artikeln, och hela strängen finns även i andra källor (se nedan).
Några tankar (ej lösning!)
Här är några tankar, där den principiella förutsättningen är att det en relativt enkel form av kodning och inte någon superkryptometod.
En tanke är att det finns tre separata delar (bokstäverna helt enkelt verkar tillhöra olika delar) som är kodade med olika typer av tekniker:
1. smithycode
2. Jaeiextostgpsacgream
3. qwfkadpmqzv
2 känns som det skulle kunna vara något anagram (på latin?). Problemet med anagram är att de tenderar att ha väldigt många lösningar så det är troligen inte rätt väg. Internet Anagram Server hittar dock inget anagram på latin. På engelska finns det däremot många (obs. stor sida!).
3 kanske är någon form av rotationskryptering. Här är 0 till 25-rotationerna och dess reverser för strängen "qwfkadpmqzv":
rot(0): qwfkadpmqzv reverse: vzqmpdakfwq
rot(1): rxglbeqnraw reverse: warnqeblgxr
rot(2): syhmcfrosbx reverse: xbsorfcmhys
rot(3): tzindgsptcy reverse: yctpsgdnizt
rot(4): uajoehtqudz reverse: zduqtheojau
rot(5): vbkpfiurvea reverse: aevruifpkbv
rot(6): wclqgjvswfb reverse: bfwsvjgqlcw
rot(7): xdmrhkwtxgc reverse: cgxtwkhrmdx
rot(8): yensilxuyhd reverse: dhyuxlisney
rot(9): zfotjmyvzie reverse: eizvymjtofz
rot(10): agpuknzwajf reverse: fjawznkupga
rot(11): bhqvloaxbkg reverse: gkbxaolvqhb
rot(12): cirwmpbyclh reverse: hlcybpmwric
rot(13): djsxnqczdmi reverse: imdzcqnxsjd
rot(14): ektyordaenj reverse: jneadroytke
rot(15): fluzpsebfok reverse: kofbespzulf
rot(16): gmvaqtfcgpl reverse: lpgcftqavmg
rot(17): hnwbrugdhqm reverse: mqhdgurbwnh
rot(18): ioxcsvheirn reverse: nriehvscxoi
rot(19): jpydtwifjso reverse: osjfiwtdypj
rot(20): kqzeuxjgktp reverse: ptkgjxuezqk
rot(21): lrafvykhluq reverse: qulhkyvfarl
rot(22): msbgwzlimvr reverse: rvmilzwgbsm
rot(23): ntchxamjnws reverse: swnjmaxhctn
rot(24): oudiybnkoxt reverse: txoknbyiduo
rot(25): pvejzcolpyu reverse: uyploczjevp
där det enda jag hittar är "warn" för reverse(rot(1)). Inget att hänga i julgranen, alltså.
Hmm, det där "y":et i "smithycode" kanske är en ledtråd...
(Tack Jonas för Expressen-länken.)
Se även
Dokumenten att leka med: Sammanfattningen. och själva domen (PDF).
Reuters: Latest Da Vinci mystery: judge's own secret code
Slashdot (naturligtvis) Judge Creates Own Da Vinci Code.
Posted by hakank at 07:15 EM Posted to Pyssel | Comments (2)
april 25, 2006
Blogglunch söndagen tjugotredje april tjugohundrasex/tvåtusensex/i år
Med:
Åsa, Thebe, Mats, Tommy, Henrik, Håkan.
Inte mat utan bloggserviett å därför avsedd pappersmaterial:
På utrymmet nedan skulle det förevisas fotografier på deltagarna fotograferandes andra deltagare symboliserande myten att bloggare endast bloggar om andra bloggar. Så blev det inte.
Posted by hakank at 05:50 EM Posted to Bloggmiddagar | Comments (5)
april 22, 2006
Divisorträd: unika sätt att göra konsekutiva uppdelningar
Vilka - och hur många - unika sätt kan man göra följande "konsekutiva delningar" av ett antal saker. Tänk t.ex. på de olika unika sätt man kan dela upp N antal spelkort i olika högar. Metoden man arbetar med är följande:
- börja med en hög av N saker
- dela upp dessa saker i ett antal högar så att det är lika många saker i varje hög
- ta en av dessa högar och fortsätt på samma sätt tills det bara finns
en sak i varje hög
Eller på ett något mer matematiskt språk: på vilka - och hur många - olika unika sätt man kan dela upp ett tal i dess divisorer (förutom 1 och talet själv).
Not: Eftersom nedanstående inte har (matematiskt) bevisats så är det endast en hypotes (en förmodan).
Uppdatering. Hmm, jag har hittat en inkonsekvens i nedanstående. Inte bra. Återkommer...
Program: Divisor tree
Det program som används för att undersöka dessa konsekutiva delningar är Divisor tree / / Consecutive dealing in heaps. Nedanstående förklaringar är förhoppningsvis tillräckligt för att förklara programmet.
Notera att programmet endast arbetar med värden mellan 2 och (lite halv godtyckligt) 30000 av datorsnällhetsskäl.
Inledande exempel
Låt oss göra det mer åskådligt med 16 saker (t.ex. 16 spelkort).
För N = 16 finns det 4 olika sätt.
16 / 2 heaps = 8 things in each heap (2 -> 8 -> ..)
8 / 2 heaps = 4 things in each heap (2 -> 4 -> ..)
4 / 2 heaps = 2 things in each heap (2 -> 2 -> 1)
8 / 4 heaps = 2 things in each heap (4 -> 2 -> 1)
16 / 4 heaps = 4 things in each heap (4 -> 4 -> ..)
4 / 2 heaps = 2 things in each heap (2 -> 2 -> 1)
16 / 8 heaps = 2 things in each heap (8 -> 2 -> 1)
Found 4 ways for N = 16.
Beskrivning av det första (unika sättet):
* Först har vi 16 saker.
* Dessa delas upp i två högar med 8 saker i varje hög.
* Vi tar en av dessa två högar och har nu en hög med 8 saker. Denna delar vi upp i 2 högar så vi får 4 saker i varje hög.
* Vi tar en av dessa högar och delar upp i 2 högar med två saker i varje hög.
* Vi tar sedan en av dessa högar och delar ut i 2 högar med 1 sak i varje hög.
Men sedan kan vi inte gå vidare eftersom det nu är endast 1 sak i varje hög. Man skulle i och för sig kunna dela upp 1 sak i 1 hög i det oändliga men det är inte tillåtet i detta spel. Regel: När det endast finns 1 sak i en (färdigutdelad) hög är man klar med denna uppdelnin.
Antal saker som fanns i de högar vi använder under utdelningen är: 16, 8, 4, 2, (1).
Tittar vi på exempelkörningen ser vi att en unik väg (ett unikt sätt) är avslutat om raden avslutas med -> 1. Står det däremot -> .. så fortsätter uppdelningen och man går vidare till nästa (inskjutna) rad. Denna trädliknande struktur är anledningen till att det kallas för divisorsträd där de olika uppdelningssätten grenar ut sig. (Möjligen skulle det kunna kallas för divisorsstad eftersom det är vägar vi pratar om eller divisorsskog efterom det är flera träd med olika grenar, men ingendera av dessa känns lika naturligt som -träd).
De 4 olika sätten för N = 16 är följande, där talen anger antal saker i varje hög. Den första raden motsvarar alltså den långa beskrivningen ovan.
16 -> 8 -> 4 -> 2
16 -> 4 -> 2
16 -> 4 -> 2
16 -> 8 -> 2
För N=12 finns det 5 vägar (avslutas med 2 eller 3)
12 / 2 heaps = 6 things in each heap (2 -> 6 -> ..)
6 / 2 heaps = 3 things in each heap (2 -> 3 -> 1)
6 / 3 heaps = 2 things in each heap (3 -> 2 -> 1)
12 / 3 heaps = 4 things in each heap (3 -> 4 -> ..)
4 / 2 heaps = 2 things in each heap (2 -> 2 -> 1)
12 / 4 heaps = 3 things in each heap (4 -> 3 -> 1)
12 / 6 heaps = 2 things in each heap (6 -> 2 -> 1)
Found 5 different way(s) for n = 12.
Primtal
Om det finns ett primtal antal saker i en hög finns det endast ett sätt (en väg) att dela upp i lika antal högar, nämligen att dela så att det finns en sak i varje hög. T.ex. om man har 13 kort så kan man endast dela ut dem i 13 olika högar med 1 kort i varje hög.
En väg avslutas alltså om det blir en hög innehåller primtal stycken saker. Eller mer korrekt: Om det är primtal antal stycken blir nästa uppdelning så många högar med 1 sak i varje hög.
Primtalskvadrater
För 4 saker så finns det bara ett sätt: nämligen att dela upp i två högar med två saker i vardera.
4 / 2 heaps = 2 things in each heap (2 -> 2 -> 1)
Found 1 different way(s) for n = 4.
Detta är ingen slump. För varje kvadrat av primtal (2^2=4, 3^2=9, 5^2=25, 7^2=49 osv) så finns det endast ett sätta att göra uppdelningen.
Båda dessa specialfall, primtal och primtalskvadrater utnyttjas i den rekursiva algoritm för att räkna ut antalet unika konsekutiva uppdelningar, och som beskrivs nedan.
Antal uppdelningar, heltalssekvenser
Om man nu räknar antalet unika sätt att göra denna typ av uppdelningar för N = 1.. 32 får vi följande heltalssekvens:
1,1,1,1,1,2,1,2,1,2,1,5,1,2,2,4,1,5,1,5,2,2,1,12,1,2,2,5,1,9,1,8
Här är en graf över sekvensen för N = 1 .. 512:
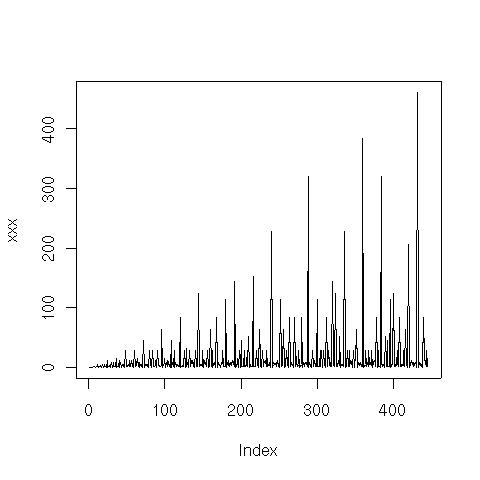
Ett bra sätt att analysera denna typ av matematiska (eller algoritmiska) strukturer är att se om det finns andra strukturer som har samma heltalssekvens. Det gör man lämpligen via On-Line Encyclopedia of Integer Sequences (som beskrivits tidigare i Heltalssekvenser). Ovanstående sekvens fanns inte med! Inte heller hittades sekvensen via superseeker som är en tjänst där man mailar in sekvensen och där systemet gör väldigt många olika typer av transformationer av sekvensen. Inte heller där hittades sekvensen.
Så det verkar som om ovanstående sekvens är ganska ovanlig. Lite märkligt eftersom det känns som en "naturlig" metod. Vi ser nedan att det är en "kusin" till en känd heltalssekvens.
Rekursiv definition
Ovanstående sekvens räknades ursprungligen ut genom att skapa vägarna i en tidig version av programmet Divisor tree, men sedan skapades (upptäcktes) en metod för att räkna ut dessa värden mycket enklare. Här är pseudokoden för metoden:
divtree(n):
# n > 0
if n == 1 then value = 1 # specialfall för n = 1
elsif prime(n) then value = 1 # primtal
else if prime_square(n) then value = 1 # kvadrat av ett primtal
else if # annars: loop igenom divisorerna av n
for div = divisors(n) do
next if div == 1 or div == n # se kommentaren nedan
value = value + divtree(div) # summera divisorernas värden rekursivt
return value
Notera raden med "next" i for-loopen. Den innebär att om divisorn är 1 eller n så adderar man inte något värde för denna divisor. (Det är genom att förändra next-raden som vi hittar sekvensens kusin. Se nedan) Notera också att det är en rekursiv definition.
Pratversionen av metoden är ungefär: Om N är 1, ett primtal eller en primtalskvadrat så finns det ett unikt sätt att göra en delning. Om N är något annat så summerar man divtree-värdena för N:s divisorer (alla divisorer förutom 1 och N själv).
Det tarvar kanske ett exempel på detta, så låt oss titta på N = 24 (dvs 24 saker). Först divisorsträdet:
24 / 2 heaps = 12 things in each heap (2 -> 12 -> ..)
12 / 2 heaps = 6 things in each heap (2 -> 6 -> ..)
6 / 2 heaps = 3 things in each heap (2
Posted by hakank at 11:09 FM Posted to Matematik | Program | Comments (2)
april 19, 2006
de Bruijn-sekvenser av godtycklig längd
För några år sedan skrevs ett program för att skapa de Bruijn-sekvenser, som kortfattat kan förklaras som en sträng (cykel) som innehåller ("testar") alla förekomster av delsträngar, där delsträngarna är representationer av tal. Mer förklaringar och exempel ges i de Bruijn-sekvenser (portkodsproblemet) och programmet de Bruijn sequence. I slutet finns även några andra referenser.
De metod som dessa sekvenser konstrueras ger endast stränglängder med jämna potenser, dvs 2^2 = 3, 2^3 = 8, 3^2 = 9, 3^3 = 27 osv. En fråga som ställdes tidigt var: Kan man skapa sådana sekvenser för en godtycklig längd, t.ex. 11, 17 eller 52 och för godtycklig bas, 2, 6,11 etc? Basen är alltså den kodning av talen man använder, där.basen 2 ger en binär representation (0,1), basen 3 använder 0, 1,2 osv.
Svaret på frågan är: Visst kan man det!
Än så länge har jag dock inte kommit på en vacker algoritm som den som finns för "vanliga" de Bruijn-sekvenser. Se The (Combinatorial) Object Server, Information on necklaces, unlabelled necklaces, Lyndon words, De Bruijn sequences (i slutet på sidan finns det länkar för att ladda ner källkod).
Programmet "de Bruijn arbitrary sequences"
Programmet de Bruijn arbitrary sequences visar några av resultaten av denna undersökning. Troligen behövs lite förklaringar av programmets metoder och parametrar och sådant bistår jag så gärna med.
Metoden: slumpa cykler
Principen för att skapa dessa sekvenser är enkel: Skapa en de Bruijn-graf och slumpa fram cykler i denna graf tills en av korrekt längd hittas.
Denna slumpmässighet är det som gör att programmet inte tillåts arbeta med speciellt stora värden.
de Bruijn graf
En de Bruijn-graf är en graf där kopplingarna mellan talen (noderna) följer "de Bruijn-regeln" att ett tals suffix ska vara ett annat tals prefix i deras *-ära representation. T.ex. det binära talet 000 kan kopplas till 001, talet 001 med 010 och 011 osv. Baser större än 2 hanteras på motsvarande sätt.
Exempel: Här visas kopplingarna i grafen för n = 16 i basen 2. Inom parentes visas den binära representation av talet.
0: 0 1 (0000)
1: 2 3 (0001)
2: 4 5 (0010)
3: 6 7 (0011)
4: 8 9 (0100)
5: 10 11 (0101)
6: 12 13 (0110)
7: 14 15 (0111)
8: 0 1 (1000)
9: 2 3 (1001)
10: 4 5 (1010)
11: 6 7 (1011)
12: 8 9 (1100)
13: 10 11 (1101)
14: 12 13 (1110)
15: 14 15 (1111)
Här är en mer grafisk representation (skapat med programmet dot).
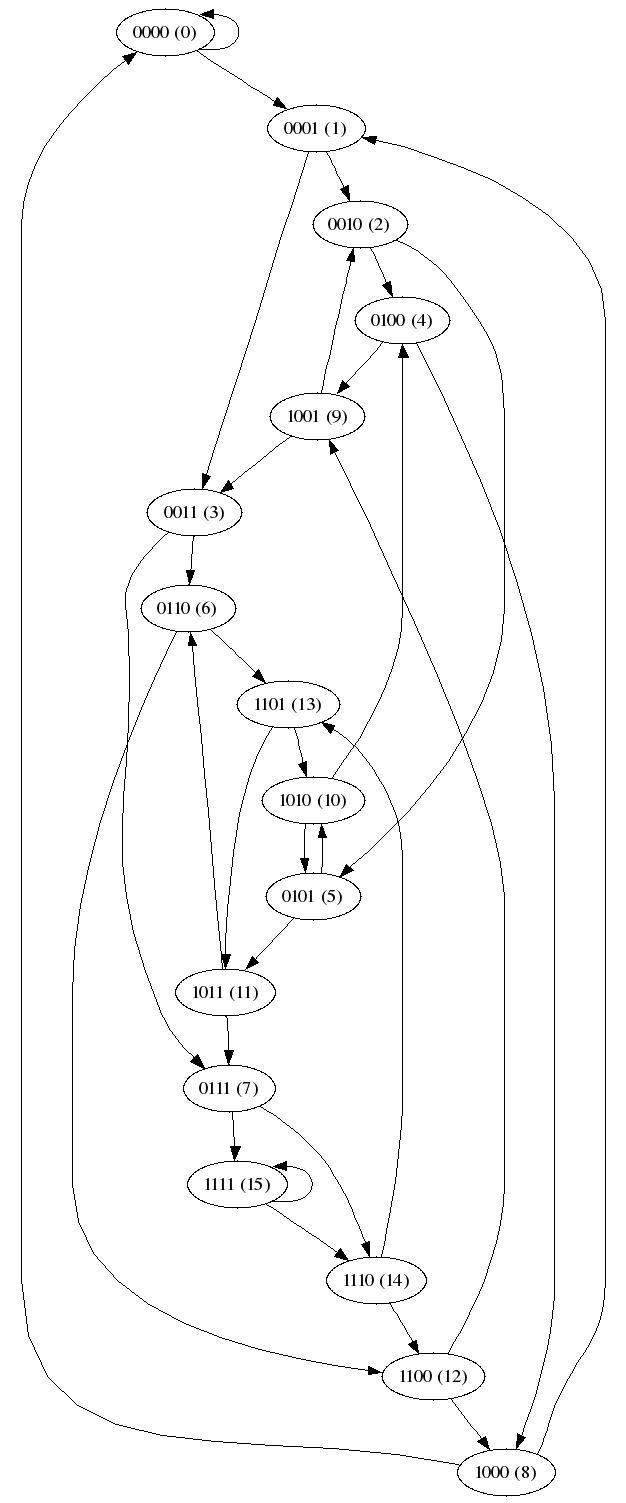 (klicka på bilden för att förstora den).
(klicka på bilden för att förstora den).
Antalet noder
Antalet noder i de Bruijn-grafen räknas ut enligt följande (motsvarar nearest_power i pseudo-koden nedan):
- om n är en jämn potens för basen används n noder (talen 0..n-1). T.ex. n=16 bas 2 är 2^3 är en sådan jämn potens.
- annars är antalet noder den närmaste efterföljande jämna potensen för basen. Exempel: För n=7 (bas 2) blir det 8 noder (2^3=8 ). För n=21 bas 3 blir det 27 noder (3^3=27 ) osv.
Kopplingsgrafen är enkel att räkna ut och principen ses nog vid närmare granskning av några exempel. Hur som helst kommer här pseudo-kod:
# nearest power in the choosen base, or N itself if N is a power
next_pow = nearest_power(N, base)
half_pow = next_pow / base;
for num (0..next_pow-1) {
for b (0..base-1) {
x = base * (num % half_pow);
conn = x + b;
graph->add_edge(num, conn); # connect num -> conn
}
}
Kort förklaring av programmet
Programmet har en del parametrar vilka här förklaras.
N (2..64): Det är stränglängden (eller antal objekt). Kan vara mellan 2 och 64.
Base (2..4): Basen som ska användas. T.ex. för bas 2 är det binär representation (0,1). Giltiga värden är 2,3 eller 4.
Type: normal / reversed: Normal innebär att sekvensen visas normalt från vänster till höger och de binära (bas-ära) talen kodas normal (7 binärt är "0111"). Det lägsta talet börjar decimalcykeln. Reversed är då man vänster på allting: de binära (etc) koderna är omvända (7 visas som "1110") och det högsta talet i decimalcykeln visas först.
Show connections: Visar kopplingarna för den de Bruijn-graf som byggs upp.
Show sequence: Här visas de individuella representationerna.
Exempel
Här är ett exempel på på en av många möljiga sekvenser för n = 52 i basen 4:
Sequence:0001012131301132230220330300323123212013332002102331
Cycle (in decimal): 0 1 4 17 6 25 39 29 55 28 49 5 23 30 58 43 44 50 10 40 35 15 60 51 12 48 3 14 59 45 54 27 46 57 38 24 33 7 31 63 62 56 32 2 9 36 18 11 47 61 52 16
Sequence check:
000101213130113223022033030032312321201333200210233100
000 (0)
001 (1)
010 (4)
101 (17)
012 (6)
....
Begränsningar
Som ovan nämnts bygger programmet på en slumpning av cyklerna. Det kan ta en stund att slumpa fram cykler av korrekt längd i stora grafer så finns det några begränsningar för att datorn inte ska bli sönderkörd:
N: mellan 2 och 64
base: mellan 2 och 4
Om någon läsare nu (eller sedan) upplever ett starkt behov av sådana sekvenser med större längd / bas så är det bara att kontakta mig (hakank@bonetmail.com så kan vi säkert ordna något.
Vidare utveckling
Denna slumpmässiga metod fungerar om det är relativt små värden av N och bas. Men för större värden är det inte en tillgänglig metod. I stället bör en deterministisk algorim skapas.
Ett pågående projekt är också att försöka minska antalet noder i grafen så att det inte blir så många möjliga cykler att leta igenom.
Not
Jag är osäker på om ovanstående fortfarande kan kallas för en de Bruijn-sekvens när man använder denna alternativa approach.
Se även
de Bruijn sequence (den "vanliga" formen)
de Bruijn-sekvenser (portkodsproblemet)
MathWorld deBruijnSequence
COS: Information on necklaces, unlabelled necklaces, Lyndon words, De Bruijn sequences
Posted by hakank at 06:52 EM Posted to Matematik | Program
april 18, 2006
Choco: Constraint Programming i Java
Bakgrund
Mitt intresse för Constraint Programming (CP) (som tidigare kallades Constraint Logic Programming, CLP) väcktes för ett antal år sedan strax efter en företagskamp (som kort beskrevs i Uppdaterat program: AnaCheck), där ett av uppdragen var följande matematiska pyssel:
Vilken är den minsta differensen man kan få mellan två tal om man måste använda samtliga siffror (0..9) exakt en gång?
Lösningen presenteras nedan.
Ungefär samtidigt stötte jag på Constraint (Logic) Programming och med detta och liknande pyssel i bakhuvudet, och blev väldigt fascinerad av programmeringsparadigmet. Kanske inte så förvånande eftersom många standardexempel är just matematiska pyssel.
Tanken är att man endast behöver skriva de problemspecifika villkoren (constraints), sedan får systemet lista ut bästa sättet att lösa problemet. Det finns många olika metoder och heuristiker för att lösa problemen, och ibland måste hjälpa till så att lösningen kommer denna sidan regnbågen eftersom vissa problem är mycket tunga.
Ett citat som ofta nämns i sammanhanget är Eugene C. Freuder (CONSTRAINTS, April 1997)
Constraint programming represents one of the closest approaches computer science has yet made to the Holy Grail of programming: the user states the problem, the computer solves it..
Prologbaserade system
I början arbetade jag mestadels med logikprogramspråket Prolog som "moderspråk", Sicstus Prolog samt ECLiPSe Constraint Programming System (det senare inte att förväxlas med utvecklingsmiljön med ungefär samma stavning).
Imperativa språk
Som komplement till de Prologbaserade systemen har jag letat efter mer imperativa - samt icke-kommersiella - moderspråk såsom Java, C, C++, Perl, Python, eftersom vissa saker är lättare att programmera med sådana språk (men ibland svårare) En av dessa implementationer Python-constraint och nämns i kommentarerna till Sesemans matematiska klosterproblem samt lite Constraint Logic Programming.
Choco
Så till det system jag har kollat i nyligen: det Java-baserade Choco. I slutet av anteckningen finns fler referenser.
Choco är snabbt och det har en stor mängd funktioner. Exemplen nedan är endast för "finita domäner" (löses med hjälp av heltal), men det finns även domäner med reella tal samt mängder.
Det är dock inte lika elegant att skriva constraints som i Sicstus/ECLiPSe, vilket vi nu kommer att titta på.
Minsta differensproblemet - en jämförelse av kodskrivning
För att tydliggöra skillnader och likheter mellan Choco och de Prologbaserade systemen visas hur minsta differensproblemet kan lösas i respektive system.
I ECLiPSe skriver man själva constraint-delen av problemet på följande sätt; i Sicstus Prolog skriver man snarlikt. Obs: koden är inte riktigt komplett att bara köra.
:-lib(fd), lib(fd_search), lib(fd_global),lib(fd_domain).
% ....
LD = [A,B,C,D,E,F,G,H,I,J], % deklarera de 10 variablerna
LD :: [0..9], % intervallet för variblerna, mellan 0 och 9
fd_global:alldifferent(LD), % alla värden ska vara olika
%
% constraints
%
% A + B + C + D + E = F + G + H + I + J
X #= 10000*A+1000*B+100*C+10*D+E,
Y #= 10000*F+1000*G+100*H+10*I+J,
% differensen ska bli positiv
X #< Y,
% differensen
Diff #= Y - X,
% minimera differensen (Diff) samt heuristik för att hitta lösningen snabbt
minimize(search(LD,0,anti_first_fail,indomain_max,credit(64,bbs(15)),[]),Diff).
Elegant och lite magiskt, eller hur?
Motsvarande Choco-program är lite längre, främst eftersom det saknas syntaktiskt socker. Det går att pressa antalet rader (sådant har gjorts) men här görs en mer expressiv form för att jämförelsen ska bli tydligare. Programmet finns att ladda ner här nedan.
// Choco program
import choco.Problem;
import choco.*;
import choco.integer.*;
public class LeastDiff {
public static void main(String[] args) {
new LeastDiff().puzzle();
}
public void puzzle () {
Problem pb = new Problem();
// definiera variablerna A .. J så att dess värden är mellan 0 och 9
IntDomainVar A = pb.makeEnumIntVar("A", 0, 9);
IntDomainVar B = pb.makeEnumIntVar("B", 0, 9);
IntDomainVar C = pb.makeEnumIntVar("C", 0, 9);
IntDomainVar D = pb.makeEnumIntVar("D", 0, 9);
IntDomainVar E = pb.makeEnumIntVar("E", 0, 9);
IntDomainVar F = pb.makeEnumIntVar("F", 0, 9);
IntDomainVar G = pb.makeEnumIntVar("G", 0, 9);
IntDomainVar H = pb.makeEnumIntVar("H", 0, 9);
IntDomainVar I = pb.makeEnumIntVar("I", 0, 9);
IntDomainVar J = pb.makeEnumIntVar("J", 0, 9);
IntDomainVar[] letters = {A,B,C,D,E,F,G,H,I,J};
IntDomainVar Diff = pb.makeBoundIntVar("Diff", 0, 10000);
// Temporära variabler
IntDomainVar X = pb.makeBoundIntVar("X", 0, 100000);
IntDomainVar Y = pb.makeBoundIntVar("Y", 0, 100000);
// alla värden ska vara unika
for (int i = 1; i <= 9; i++) {
for (int j = 0; j <= 9; j++) {
if (i==j) {
continue;
}
pb.post(pb.neq(letters[i], letters[j]));
}
}
// X = A+B+C+D+E
pb.post(pb.eq(X, pb.scalar(new int[]{10000, 1000, 100, 10, 1},
new IntDomainVar[]{A,B,C,D,E})));
// Y = F +G + H + I + J
pb.post(pb.eq(Y, pb.scalar(new int[]{10000, 1000, 100, 10, 1},
new IntDomainVar[]{F,G,H,I,J})));
// Diff = X - Y
pb.post(pb.eq(pb.minus(X, Y), Diff));
// minimera skillnaden
pb.minimize(Diff,false);
// nu ska vi lösa problemet
Solver s = pb.getSolver();
pb.solve(true);
// Skriv ut lösningen
System.out.println("Result: "+ A.getVal() + B.getVal() + C.getVal() +D.getVal() + E.getVal() + " - " + F.getVal() + G.getVal() + H.getVal() + I.getVal() + J.getVal() + " = " + Diff.getVal() );
} // end puzzle
} // end class
Lösningen som ges av dessa båda program är samma, nämligen
50123 - 49876 = 247
Några körbara (kompilerbara) Choco-program
Här är källkoden till några andra mindre Choco-program, varav några är standardproblem inom constraint programming. Choco-distributionen innehåller några andra.
LeastDiff2.java: Ovanstående exempel
FurnitureMoving.java: Planering av möbelflyttande, använder cumulative.
Knapsack.java: ett enkelt knapsack-problem (minimize)
Zebra.java: ett standardpyssel
Seseman.java: Choco-versionen av Sesemans matematiska klosterproblem
Se även
om Choco:
Choco: projektsidan på Sourceforge
Wiki
User guide
Choco API
Forum
om constraint programming
Roman Barták: On-line Guide to Constraint Programming
Roman Barták: Constraint Programming: In Pursuit of the Holy Grail (PDF)
tidigare skrivet om C(L)P
Sesemans matematiska klosterproblem samt lite Constraint Logic Programming
Automatisk "lösning" av Minesweeper i Mozart/Oz
JaCoP är ett annat Javabaserat system, utvecklat vid Lunds Universitet som man kan få tillgång till om man frågor någon av dess skapare. Har inte kollat in det så mycket ännu, men det verkar också trevligt.
Posted by hakank at 09:59 EM Posted to Constraint Programming | Matematik | Pyssel
april 17, 2006
Mutt - en konfigurerbar mailklient
I mer än 10 år har jag läst merparten av privata mail med den textbaserade mailklienten Pine. I den gångna veckan bytte jag till en annan textbaserad editor: Mutt (*).
Eftersom pålitliga vänner länge har pratat väl om Mutt har jag kikat på det flera gånger tidigare. Trådning har alltid varit ett stort argument, liksom konfigurerbarheten. Men det har alltid varit för meckigt och icke prioriterat att byta till ett annat mail-läsarsystem.
Efter att ha bitit i det sura äpplet (byte av den Linux-maskin där jag läser mail och där installation av Pine tjorvade) började jag alltså lära mig Mutt från grunden. Redan efter några minuter påträffades saker som jag nu inte förstår hur jag kunde klara mig utan. T.ex. att kunna ange vilken mailbox som ska föreslås som default när man sparar ett läst mail (s.k. save-hook, baserat på information i header-fälten, se nedan); de kraftfulla sökmöjligheterna samt naturligtvis trådningen av mailen.
Här är några för mig användbara saker från min nuvarande konfigurationsfil (.muttrc) varsamt kommenterad. Även om det inte syns så motstod jag frestelsen att definiera om Mutt så det liknar Pines tangentkonfiguration. Det mesta känns logiskt.
# använd textläges-emacs som editor
set editor="emacs -nw"
# när man läser mail ser man delar av maillistningen
# man kan toggla detta via macrot på I, se nedan
set pager_index_lines=8
# togglar om man ska se maillistningen när man läser ett mail.
# de två första är "interna funktioner" (Inspiration från Roland Rosenfeld)
macro pager _TOGIL0 ':set pager_index_lines=0
macro pager _TOGIL1 ':set pager_index_lines=9
# Finns på I (versalt i)
macro pager I _TOGIL0 'toggle pager_index_lines'
# redigera .muttrc
# kan göras dels i listningen av mail och när man läser ett mail
macro pager
macro index
# laddar om .muttrc. Notera att gamla alias etc finns kvar efter omladdning.
macro index
macro pager
# gå tillbaka till "första sidan", dvs den vanliga inboxen
macro pager Q 'c !<enter>' 'till huvudsidan'
macro index Q 'c !<enter>' 'till huvudsidan'
# definieras något annorlunda i browsern (fil/folderlistningen)
macro browser Q 'q !<enter>' 'till huvudsidan'
# grepm är ett externt program som möjliggör sökning i flera foldrar samtligt.
# Kräver grepmail
# (skriv in sökkriteriet och tryck sedan Enter)
macro index
# kopia av skickade mail sparas i en sent-mail-YYYY-MM-folder
set record="=sent-mail-`date +%b-%Y`"
# Fråga inte "move read messages to mbox" när vid avsluta
set move=no
# Fråga inte om man man ska "append to mailboxes" vid spara
set confirmappend=no
# exempel på några save-hooks: När man sparar ett läst mail kommer en speciell
# mailfolder som förslag. (För att spara mail till mailfoldrar utan att läsa dem används
# lämpligen t.ex. procmail.)
# Förklaring:
# ~f: From-fältet, ~t: TO, ~c: CC, ~h finns i någon header
#
save-hook "~t CRYPTO-GRAM-LIST@LISTSERV.MODWEST.COM" =crypto-gram
save-hook "~f comdig@ms68.hinet.net" =complexity_digest
save-hook "~h noreply-orkut@google.com" =orkut
# sorteringsordning baserad på den folder man är i
# trådning är default
folder-hook . set sort=threads
# men i spam-foldern sorteras i datumordning, senaste mailet först
folder-hook caughtspam set sort=-reverse_date
# folderlistan sorteras om omvänd datumordning
set sort_browser=reverse-date
# default vid q (quit) är No i stället för det fabriksinställda Yes
set quit=ask-no
# piper när nya meddelanden kommer i mailboxes (se nedan)
set beep_new=yes
# Förutom inkommande-foldern definieras även dessa foldrar som mailfoldrar när nya mail
# kommer in automatiskt t.ex. via procmail
# Det innebär att det piper när det kommer nya mail , de hanteras speciellt
# i folderlistan, att man via kommandot "." (punkt) ser om det kommit nya mail etc
# Not: det är anonymiserade foldernamn.
mailboxes =folder1 =folder2 =folder3
En sak störde mig stort från början och det var att Ctrl-C (för att avbryta en operation) alltid frågade om man vill avsluta Mutt och default var att det ville jag. Men det ville inte jag; jag ville inte ens ha frågan. Tyvärr hittades inget konfigurationskommando för att styra detta beteende, varpå frågan sonika kommenterades bort i källkoden (funktionen mutt_query_exit i i curs_lib.c). Nu händer alltså inget mer än att operationen avbryts, vilket är den intuition jag har kring hur Ctrl-C ska fungera i detta sammanhang.
(*) Ja, jag läser hellre privata mail i en textbaserade mailklient än på andra sätt. Gmail är trevlig liksom Evolution, men inte tillräckligt trevliga. Det finns för- och nackdelar med respektive lösningar.
Se även
MuttWiki
comp.mail.mutt.
Tips: Via "Prenumerera på den här gruppen" och sedan "Sammandragsmail (hela meddelanden) " blir man mailad nya inlägg i gruppen cirka en gång per dag.
Yahoo! mutt-users
Manualen till version 1.5.11
Utvecklingsversionen (CVS).
Exempel på konfigurationsfiler (från Wikin)
dotfiles.com har fler exempel på konfigurationsfiler.
mutt next generation, en variant av Mutt med extra features. (Att kika mer på.)
procmail för att automatiskt filtrera mail till mailboxar. Kombineras lämpligen med ett spamupptäckarprogram, t.ex. Spamassassin.
Posted by hakank at 08:17 FM Posted to Program | Comments (1)
april 16, 2006
Ny webbserver
Efter väldigt många års trogen tjänst drog den gamla webbservern sin sista suck. En ny server är alltså uppe.
Av lite olika anledningar har några av de senaste inläggen försvunnit. Möjligen kommer de tillbaka. Några av dem finns att tillgå via googles cache av bloggen. Uppdatering: Nu är de gamla anteckningarna återskapade, och denna anteckning har skrivits om (inklusive kommentarerna) . Möjligen stökar detta till det för sökmotorer eller aggregerare.
Ser ni några konstigheter på sajten (förutom att det går snabbare) är jag tacksam om ni rapporterar till hakank@bonetmail.com.
Posted by hakank at 10:56 FM Posted to Blogging | Comments (6)