Via the post
A New Twist on Latin Squares from the interesting math blog
360, I learned the other day about a new grid puzzle Strimko, based on Latin squares (which for example Sudoku also is).
The
rules of Strimko are quite simple:
Rule #1: Each row must contain different numbers.
Rule #2: Each column must contain different numbers.
Rule #3: Each stream must contain different numbers.
The
stream is a third dimension of the puzzle: an connected "stream" of numbers which also must be distinct.
Here is an example of a Strimko puzzle (weekly #068, same as in the 360 post):
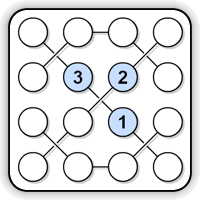
(the link goes to a playable version).
MiniZinc model
This problem was simple to solve in MiniZinc:
strimko.mzn, and the data file
strimko_068.dzn.
Here are the constraints of the model: three calls to
all_different, one for each rows, cols (these two are the latin square requirement), and also for each stream. The
places is for handling the "hints" (the given numbers) in the puzzle.
constraint
% latin square
forall(i in 1..n) (
all_different([ x[i, j] | j in 1..n]) /\
all_different([ x[j, i] | j in 1..n])
)
/\ % streams
forall(i in 1..n) (
all_different([x[streams[i,2*j+1],streams[i,2*j+2]] | j in 0..n-1])
)
/\ % placed
forall(i in 1..num_placed) (
x[placed[i,1], placed[i,2]] = placed[i,3]
)
;
The data file
strimko_068.dzn is shown below:. Note the representation of the puzzle: Each cell is represented with two numbers,
row,column.
% Strimko Set 068
n = 4;
streams = array2d(1..n, 1..n*2, [
1,1, 2,2, 3,3, 4,4,
2,1, 1,2, 1,3, 2,4,
3,1, 4,2, 4,3, 3,4,
4,1, 3,2, 2,3, 1,4
]);
num_placed = 3;
placed = array2d(1..num_placed, 1..3, [
2,2,3,
2,3,2,
3,3,1
]);
Solution:
4 2 3 1
1 3 2 4
2 4 1 3
3 1 4 2
A better version
But it was quite boring and error prone to code the problem instance in that representation. There is - of course - a simpler way by represent the streams themselves, i.e. give each stream a unique "stream number", and all cells with the same numbers must be distinct. Data file:
strimko2_068.dzn
% Strimko Weekly Set 068
streams = array2d(1..n, 1..n, [
1,2,2,4,
2,1,4,2,
3,4,1,3,
4,3,3,1
]);
% ...
The model also needed a simple change to reflect this representation:
strimko2.mzn:
% ...
/\
% streams
forall(s in 1..n) (
all_different([x[i,j] | i,j in 1..n where streams[i,j] = s])
)
% ....
The main advantage of the second model is that it makes it easier to state the problem instances. Also it is somewhat smaller to represent the grid:
n x n*2 versus
n x n. However, I haven't noticed any difference between the performance of these two models, but the problems are all very small so it may not be visible.
The problem instances
Here are all the implemented models and the problem instances:
- strimko.mzn: Strimko puzzle, first representation
Some data files:
- strimko2.mzn: Strimko puzzle, second and betterrepresentation
Some data files:
For more information about Strimko, and some problems, see:
For more about MiniZinc and some of my models, see
My MiniZinc page.
