Strimko - Latin squares puzzle with "streams"
Via the post A New Twist on Latin Squares from the interesting math blog 360, I learned the other day about a new grid puzzle Strimko, based on Latin squares (which for example Sudoku also is).
The rules of Strimko are quite simple:
Here is an example of a Strimko puzzle (weekly #068, same as in the 360 post):
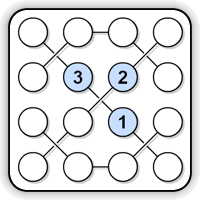
(the link goes to a playable version).
Here are the constraints of the model: three calls to
The rules of Strimko are quite simple:
Rule #1: Each row must contain different numbers.The stream is a third dimension of the puzzle: an connected "stream" of numbers which also must be distinct.
Rule #2: Each column must contain different numbers.
Rule #3: Each stream must contain different numbers.
Here is an example of a Strimko puzzle (weekly #068, same as in the 360 post):

(the link goes to a playable version).
MiniZinc model
This problem was simple to solve in MiniZinc: strimko.mzn, and the data file strimko_068.dzn.Here are the constraints of the model: three calls to
all_different, one for each rows, cols (these two are the latin square requirement), and also for each stream. The places is for handling the "hints" (the given numbers) in the puzzle.
constraint
% latin square
forall(i in 1..n) (
all_different([ x[i, j] | j in 1..n]) /\
all_different([ x[j, i] | j in 1..n])
)
/\ % streams
forall(i in 1..n) (
all_different([x[streams[i,2*j+1],streams[i,2*j+2]] | j in 0..n-1])
)
/\ % placed
forall(i in 1..num_placed) (
x[placed[i,1], placed[i,2]] = placed[i,3]
)
;
The data file strimko_068.dzn is shown below:. Note the representation of the puzzle: Each cell is represented with two numbers, row,column.
% Strimko Set 068
n = 4;
streams = array2d(1..n, 1..n*2, [
1,1, 2,2, 3,3, 4,4,
2,1, 1,2, 1,3, 2,4,
3,1, 4,2, 4,3, 3,4,
4,1, 3,2, 2,3, 1,4
]);
num_placed = 3;
placed = array2d(1..num_placed, 1..3, [
2,2,3,
2,3,2,
3,3,1
]);
Solution:
4 2 3 1 1 3 2 4 2 4 1 3 3 1 4 2
A better version
But it was quite boring and error prone to code the problem instance in that representation. There is - of course - a simpler way by represent the streams themselves, i.e. give each stream a unique "stream number", and all cells with the same numbers must be distinct. Data file: strimko2_068.dzn
% Strimko Weekly Set 068
streams = array2d(1..n, 1..n, [
1,2,2,4,
2,1,4,2,
3,4,1,3,
4,3,3,1
]);
% ...
The model also needed a simple change to reflect this representation: strimko2.mzn:
% ...
/\
% streams
forall(s in 1..n) (
all_different([x[i,j] | i,j in 1..n where streams[i,j] = s])
)
% ....
The main advantage of the second model is that it makes it easier to state the problem instances. Also it is somewhat smaller to represent the grid: n x n*2 versus n x n. However, I haven't noticed any difference between the performance of these two models, but the problems are all very small so it may not be visible.
The problem instances
Here are all the implemented models and the problem instances:- strimko.mzn: Strimko puzzle, first representation
Some data files: - strimko2.mzn: Strimko puzzle, second and betterrepresentation
Some data files:
Comments
Thank you very much for the great article about our Strimko puzzle concept! We very appreciate it.
Currently we'd like to inform you about unprecedented fact in the puzzling world connected with Strimko. On August 10, 2009, Conceptis Puzzles launched a "new" puzzle concept which they call Chain Sudoku (http://www.conceptispuzzles.com/index.aspx?uri=info/news/315). It's nothing else than well know Strimko concept which they simply STOLE, and now use without any authorization or licence from its creators - The Grabarchuk Family. I'm sorry to disturb you with this matter, but I thought you must know about this extraordinaire (and quite puzzling) fact.
BTW, there is very interesting discussion about this matter on theirs forum http://www.conceptispuzzles.com/forum/tm.aspx?m=30411&mpage=1&key=%26%2330434%3B.
Best Regards,
Peter Grabarchuk
The Grabarchuk Family
www.grabarchukpuzzles.com
Posted by: Peter Grabarchuk | August 12, 2009 05:25 PM
You say: "However, I haven't noticed any difference between the performance of these two models, but the problems are all very small so it may not be visible.".
Well, I haven't use Minizinc, but by analogy with other modeling language I would assume that the expression "x[i,j] | i,j in 1..n where streams[i,j] = s" is evaluated once and for all when constructing the constraints. So the constraints constructed in both models are exactly the same, hence I'd say there's only one model here, not two.
Assuming constructing the problem takes a small time compared to solving it, it's then expected that the performance is the same in both cases.
Posted by: K | August 12, 2009 05:25 PM
K: Thanks for your comment.
It is probably a matter of definition of "model" here, but since there are two different representations of data it is - trivially - two different programs ("scripts").
You have a point, of course.
Both "programs" generates the same number of "all_different" constraints, and - except for the indices in the data arrays - they represent the same cells.
Thanks for the clarification.
Posted by: hakank![[TypeKey Profile Page]](http://www.hakank.org/constraint_programming_blog/nav-commenters.gif) |
August 12, 2009 06:18 PM
|
August 12, 2009 06:18 PM
Peter: Thanks for your comment, and for a great puzzle!
Let's hope that the copyright issues will be settled soon.
Posted by: hakank![[TypeKey Profile Page]](http://www.hakank.org/constraint_programming_blog/nav-commenters.gif) |
August 12, 2009 06:41 PM
|
August 12, 2009 06:41 PM